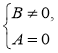Урок, "Раціональні рівняння"

Про матеріал

Цель: Добиться усвоения учащимися содержания понятий: «рациональное уравнение». Сформировать у учащихся представление о содержании понятия «ОДЗ уравнения», роль его в построении общей схемы решения дробно-рационального уравнения и о самой схеме решения дробно-рационального уравнения. Сформировать умение отличать изученные виды уравнений друг от друга и аргументировать свое мнение; находить, используя содержание понятия, ОДЗ уравнения, а также решать простейшие дробно-рациональные уравнения по изученной схеме. Развивать логическое мышление, память в ходе повторения изученного материала. Воспитывать культуру речи, патриотизм в процессе просмотра тематического видео из жизни великих украинцев.

Перегляд файлу

Алгебра 8 класс

Тема. Рациональные уравнения. Решение рациональных уравнений

Тип урока: усвоение знаний и первичных умений.

Наглядность и оборудование: опорный конспект «Рациональные уравнения», мультимедийная презентация, раздаточный материал.

Ход урока

I. Организационный этап

II. . Актуализация опорных знаний и умений

С целью успешного восприятия учащимися учебного материала перед изучением новой темы при проверке д/з повторяем ранее изученный материал и слаживаем в «корзину знаний»

Фронтальный опрос: на слайдах

определение целых и дробных рациональных выражений;
ОДЗ рационального (целого и дробного выражений);
Основное свойство дроби;
Сложение дробных выражений с одинаковыми знаменателями;
Сложение дробных выражений с разными знаменателями;
Умножение дробей;
Деление дробей;
Корень уравнения;
Что означает решить уравнение;
Алгоритм решения уравнения;
Когда дробь равна 0.

ІІІ. Проверка домашнего задания на слайдах

Тщательному разбору подлежат упражнения на применение приемов преобразования выражений, имеющих вид отношения двух рациональных выражений.

Для учеников, которые хорошо освоили приемы работы с выражениями предложено просмотреть на блоге http://sanmomatem.blogspot.com/ дополнительные задачи именно такого типа и оценить их выполнение. Решение задачи.

Турист проплыл на лодке против течения реки 6 км и по озеру 15 км, затратив на путь по озеру на 1 час больше чем на путь по реке. Зная, что скорость течения реки равна 2 км/ч, найдите скорость лодки при Условия задачи удобно анализировать, заполняя таблицу.

	Путь S (км)	Скорость V (км/ч)	Время t (ч)
Против течения
По озеру

Пусть х км/ч скорость движения лодки по озеру. По условию х > 0.

	Путь S (км.)	Скорость V (км/ч.)	Время t (ч)
Против течения	6 км	(х-2)км/ч
По озеру	15 км	х км/ч

На 1 час больше.

III. Формулировка цели и задач урока

На интуитивном уровне ученики составляют необходимые отношения и связывают их в уравнение. Приходим к выводу, что не знаем, как его решить. Оглашается тема урока и его цель: научиться решать простейшие дробно-рациональные уравнения. Поэтому учащиеся должны осознать тот факт, что изучение способов преобразования самих по себе рациональных выражений не есть самоцелью изучения алгебры, наоборот, они интересуют нас только потому, что могут быть применены в работе с другими объектами алгебры - уравнениями, которые в свою очередь является средством для решения текстовых задач. Поэтому вполне логично после изучения способов преобразований дробных рациональных выражений изучить вопрос о видах и способы решения уравнений, состоящие из таких выражений.

VІ. Усвоение знаний

План изучения нового материала

1. Определение рационального уравнения, целого рационального уравнения, дробно-рационального уравнения (с примерами и контр-примерами).

2 . Определение ОДЗ (рационального) уравнения; нахождения ОДЗ рационального уравнения.

3. Алгоритм решения дробно-рационального уравнения вида = 0 (где А и В - некоторые многочлены от одной переменной).

4. Пример применения изученного алгоритма. слайд

Опорный конспект

Рациональные уравнения

Алгоритм решения уравнения вида = 0 (А і В — многочлены от одной переменной)

1) В ≠ 0 (найти ОДЗ уравнения):

2) А = 0 (найти, при каких значениях переменной числитель равен нулю);

3) (найти, какие с корней уравнения А = 0 удовлетворяют ОДЗ уравнения);

4) Ответ . (Записать в ответе эти корни.)

VI. Усвоение знаний

Выполнение устных упражнений (фронтальная работа) слайд

Какие из уравнений являются целыми рациональными? дробно-рациональными? (на откидной доске)

2х – 1 = 0; х² – 3х + 5 = 0; ; ; .

(коллективное обсуждение)

Прокомментируйте (используя алгоритм) решение уравнения 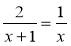. слайд

1) , , ;

2) ОДЗ: х ≠ 0 ;

х + 1 ≠ 0; ↔ х ≠ 0 ; х ≠ -1;

3) х – 1 = 0,

х = 1 — входит в ОДЗ.

Ответ: 1.

(дифференцированная индивидуальная работа )

Заполните таблицу: (учащиеся в течении 2-3 минут заполняют таблицу, обмениваются карточками, а затем сверяют с экраном ответы, при этом комментируют ответы учащиеся соответственных уровней) слайд

Уравнения	ОДЗ	Значение переменной, при котором в числителе нуль	Не входит в ОДЗ	Ответ
	х ≠
	х ≠5
	х ≠

V. Историческая справка (Из жизни М. Ф. Кравчука, видео-ролик)

VI Решение письменных упражнений (Работа группами).

В классе назначаются на каждом ряду консультанты, которые распределяют задания между группой, и цепочкой у доски три группы решают уравнения.

1) группа: а) ; б) ; в) ; г).

2) группа: а) ; б) ; в) ; г) .

3) группа: а) ; б) ; в) ; г) . Д₁); Д₂); Д₃ )

VIІ. Итоги урока

В каком из случаев правильно решено уравнение?

На откидной доске

1) ,	2) ,	3) . ОДЗ: х + 3 ≠ 0, х ≠ - 3.
х – 2 = 0, х = 2.	х + 3 = 0, х = -3.	х – 2 = 0, х = 2 — удов ОДЗ.
Ответ . 2	Ответ. -3	Ответ. 2