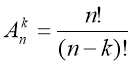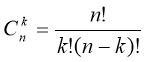Урок "Розв'язування комбінаторних задач"
Тема уроку. Розв’язування комбінаторних задач.
Мета уроку
- дидактична (навчальна): формувати уміння і навички розв’язувати різні види комбінаторних задач, застосовувати основні теореми комбінаторики – правила суми та добутку, закріпити відомі методи і способи на практиці, вчити застосовувати знання на практиці;
- розвивальна: розвиток розумових здібностей, логічного мислення, уваги і
кмітливості учнів;
– виховна: створення атмосфери емоційного підйому, співпраці; сприяння зацікавленості даною темою, історією дисципліни; формування навичок колективної праці, об’єктивного самооцінювання.
Тип уроку. Комбінований
Епіграф: «Число, положення і комбінація – три різні сфери думки, але
які взаємно перетинаються і до них можна віднести усі
математичні ідеї»
Англ. математик Дж. Сильвестр (1844р.)
Хід уроку.
І. Організаційний момент.
а) Повідомлення теми і мети заняття.
б) Перевірка домашнього завдання.
На екрані з’являються задачі домашнього завдання з відповідями. За кожну правильну відповідь учні виставляють собі в зошит 1 бал
Задачі домашнього завдання і відповіді до них.
№1 Скоротити дріб:
1) ![]() Відповідь: 30 2)
Відповідь: 30 2) ![]() Відповідь: 840
Відповідь: 840
№2 Скільки чотирицифрових чисел можна скласти з цифр: «2; 7; 8; 6»?
Відповідь: ![]()
№3 Скількома способами можна вибрати два олівця різного кольору з
дванадцяти різнокольорових олівців?
Відповідь: 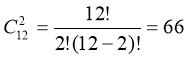
№4 Комісія складається з голови, заступника і ще п’яти осіб. Скількома
способами сім членів комісії можуть розподілити між собою обов’язки
голови і заступника?
Відповідь: 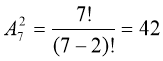
№5 Мають набори з десяти різних букв і п’яти різних цифр.
Скількома способами можна обрати:
1) одну букву або цифру? Відповідь: правило суми – 15
2) набір з однієї букви і однієї цифри? Відповідь: правило добутку – 50
Додаткові завдання.
Приклад 1.
Для захисту інформації на комп’ютері використовують пароль – послідовність літер або цифр довжиною від 3 до 5 символів (пароль може мати декілька однакових символів). Скільки різних паролів можна утворити, використовуючи 26 літер та 10 цифр?
Розв’язання.
- Пароль містить три символи. Обираємо перший символ. Маємо 36 можливостей це зробити. Для другого – теж 36, як і для третього. Тоді, за правилом множення, загальна кількість паролів дорівнює 363.
- Якщо ми вирішимо, що пароль міститиме 4 символи, то кількість різних паролів становитиме 364. Якщо ж наш вибір – 5 символів, то варіантів 365.
- Тому, за правилом суми, загальна кількість можливих варіантів паролів 363+364+365=46656+1679616+60466176=62 192 468
Приклад 2.
Скількома способами 12 осіб можна розмістити за столом, біля якого поставлено 12 стільців?
Розв’язання.
РІ2= 12! способами.12! = 479 001 600.
Вчитель. Якщо гості будуть пересаджуватися щохвилини протягом 11 год на добу 365 днів на рік з відпочинком 1 день у високосному році, то на це піде 1988 років і 140 днів.
в) Роздавання карток самоконтролю, пояснення, як з ними працювати.
|
|
Прізвище, ім’я ________________________________________ |
|||
|
Перевірка домашнього завдання
max – 7 б |
Комп’ютерне тестування
max – 11 б |
Розв’язування задачі біля дошки.
max – 4 б |
Самостійна робота з картками.
max – 8 б |
Додаткові бали |
|
|
|
|
|
|
|
Сума балів: |
||||
|
Оцінка: |
||||
У відповідну колонку картки самоконтролю учні виставляють собі суму балів за правильність виконання домашнього завдання
г) Вступне слово вчителя.
На попередніх заняттях ми отримали весь необхідний теоретичний матеріал з теми: «Комбінаторика», без якого неможливе розв’язування задач теорії ймовірності які ми будемо вивчати згодом.
Математика – це наука, оволодіти якою можна тільки через поєднання теорії з практикою. Академік О.М. Крилов сказав: «Теорія без практики мертва та безплідна, практика без теорії неможлива чи згубна. Для теорії потрібні головним чином знання, для практики, крім того, і вміння». Тому спочатку перевіримо, як ви опанували теоретичний матеріал.
ІІ. Актуалізація опорних знань.
Комп’ютерний тест
а) Математичний диктант у формі «незакінчених речень».
1. На екрані з’являються «незакінчені речення», які учні доповнюють у робочих зошитах.
Учні , що сидять поруч, обмінюються зошитами і перевіряють роботи один одного. За кожну правильну відповідь нараховується 1 бал.
2. На екрані з’являються «повні речення»
«Незакінчені речення» + «Повні речення» ( Відповіді )
1. Різні групи елементів деякої множини, що відрізняються елементами або
порядком цих елементів, називають сполуками.
2. Комбінаторика – це розділ математики, в якому вивчаються властивості сполук і формули обчислення кількості різних сполук.
3. Якщо порядком елементів сполуки між собою не відрізняються, то це – комбінації.
4. Якщо сполуки відрізняються порядком елементів і всі елементи множини входять у сполуку, то це – перестановки.
5. Якщо сполуки відрізняються і елементами, і порядком цих елементів, але не всі елементи множини входять у сполуку, то це – розміщення.
6. n! = 1∙2∙3∙ … ∙(n – 1)∙n
7. ![]()
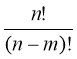 – це формула обчислення кількості розміщень.
– це формула обчислення кількості розміщень.
8. ![]() – це формула обчислення кількості перестановок.
– це формула обчислення кількості перестановок.
9. 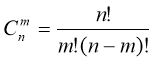 – це формула обчислення кількості комбінацій.
– це формула обчислення кількості комбінацій.
10. Якщо елемент А можна обрати m-способами, а елемент B – n-способами,
то А і В можна обрати m∙n способами. Це правило добутку.
11. Якщо елемент А можна обрати m-способами, а елемент B – n-способами,
то А або В можна обрати (m + n) способами. Це правило суми.
Учні, переконавшись у правильності оцінювання, заносять сумарну кількість балів у відповідну колонку картки самоконтролю.
б) Схема розв’язування комбінаторних задач.
Вчитель. « Ми вже розв’язували з Вами нескладні комбінаторні задачі, але насамперед знали, який вид сполук в них присутній, або яке правило: суми чи добутку треба застосувати. Тепер нам потрібно навчитися самостійно розрізняти види сполук в комбінаторних задачах. Для цього вам у нагоді стане схема розв’язування комбінаторних задач.»
Запитання:
1) В яких сполуках враховується порядок елементів? ( В перестановках і розміщеннях. В комбінаціях порядок слідування елементів не враховується. Тому це перше запитання схеми.)
2) Якщо порядок слідування елементів враховується, то отримуємо наступне запитання. В яку сполуку входять всі елементи множини? ( В перестановки.
Якщо не всі елементи входять, то обираємо останній вид – комбінації)
3) Якщо обирають елементи А і В з двох різних множин, то яке правило треба застосувати? ( Правило добутку )
4) Якщо обирають елемент А або В з двох різних множин, то яке правило треба застосувати? ( Правило суми )
|
Схема розв’язування комбінаторних задач |
|||||||
|
Вибір формули
|
|||||||
(1)
Так (2) Ні (3)
Так (4) Ні (5) |
|||||||
|
Вибір правила
|
|||||||
|
Правило суми (6) |
Правило добутку (7) |
||||||
|
Якщо елемент А можна вибрати m способами, а елемент В – n способами, то А або В можна вибрати (m + n) способами
|
Якщо елемент А можна вибрати m способами, а після цього елемент В – n способами, то А і В можна вибрати (m ∙ n) способами
|
||||||
ІІІ. Формування умінь і навичок.
а) Розв’язування задач з використанням схеми На екрані з’являються задачі.
Учні за бажанням виходять працювати до дошки, отримуючи від 1-го до 4-х балів.
Розв’язування задач
(біля дошки).
1. Скільки трицифрових чисел з різними цифрами можна скласти з набору
« 1; 2; 3; 4; 5»?
Схема: (1) – (2) – (5) 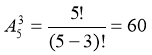
2. На площині позначено 8 точок (жодні 3 не лежать на одній прямий). Скільки існує трикутників з вершинами в цих точках?
Схема: (1) – (3) 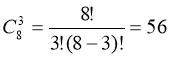
3. Скількома способами можна розставити 7 книжок на полиці?
Схема: (1) – (2) – (4) ![]()
4. З 10 учнів потрібно вибрати двох для прибирання кабінету. Скільки існує варіантів вибору?
Схема: (1) – (3) 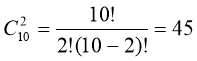
5. Розклад містить 4 уроки на день з різних 10-ти предметів. Скільки існує варіантів скласти розклад на один день(предмети не повторюються)?
Схема: (1) – (2) – (5) 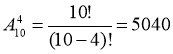
б) Хвилинка відпочинку: « З історії розвитку комбінаторики»
Викладач: З задачами, в яких приходиться вибирати ті чи інші предмети, розміщувати їх в певному порядку і відшуковувати серед різних розміщень найкращі, люди стикнулися ще в доісторичну епоху, обираючи найкращі розміщення мисливців під час полювання, воїнів під час битви, інструментів під час роботи. Пізніше, поряд із спортивними змаганнями з’явились ігри з різними фігурами чи предметами, в яких вигравав той, хто краще знав переможні комбінації та вмів уникати програшних.(Давня єгипетська гра «сенет», в яку грав фараон Тутанхамон, нарди, китайські та японські шахмати, японські шашки «го» і т. д.) Що ж було поштовхом до виникнення комбінаторики, як науки? Для чого ще потрібні знання з комбінаторики, крім відомого вже нам застосування в теорії ймовірності?
Доповіді учнів
Під час доповідей на екрані з’являються портрети вчених-математиків.
1.Перша праця, що містила комбінаторні задачі, увійшла в книгу «Книгу Абака» видатного математика Леонардо Фібоначчі в 1202 р. Наприклад, задача про пошук найменшої кількості гир, за допомогою яких можна отримати будь-яку цілу вагу від 1 до 40 фунтів.
Але поштовхом до виникнення комбінаторики був розквіт азартних ігор, зокрема гри в кості. Питаннями, що пов’язані з цією грою, займалися в ХVIст. італійські математики – Джероламо Кардано, Н. Тарталья, в ХVIІст. – Галілео Галілей, видатні математики Франції – Блез Паскаль і П’єр Ферма. Саме роботи Паскаля і Ферма дали поштовх для народження нових гілок математичної науки – комбінаторики і теорії імовірності. Вже у 1666 р. Готтфрід Вільгельм Лейбніц публікує «Дисертацію про комбінаторне мистецтво, в котрій вперше з’являється сам термін «комбінаторика». Лейбніц, якому на той час було всього 20 років і котрий мав вчений степінь з юриспруденції, планував для комбінаторики нові додатки: до кодування, статистики, теорії спостережень. Учень Лейбніца – Якоб Бернуллі в своїй книзі «Мистецтво припущень» (1713р.) виклав багато відомостей з комбінаторики та вперше увів поняття «перестановки», «розміщення». Остаточно комбінаторика як самостійний розділ математики оформилась в працях Леонардо Ейлера у ХVIІІст.
2.Для кодування таємної інформації та її розшифровки потрібні знання комбінаторики, тому для вирішення цих питань залучали математиків. Першим де шифрувальником був «батько алгебри» – Франсуа Вієт.(кінець ХVIст.) Навички в розгадці складних шифрів допомогли ученим, коли археологи почали відкопувати камені та інші предмети давнини з таємними знаками – письменністю. Таким чином і в археології комбінаторика має застосування.
Складність будови біологічних систем, взаємне поєднання окремих процесів в цілому організмі роблять біологію підходящим полем застосування комбінаторних методів. Поєднуючи їх з вивченням рентгенівських знімків, вченим вдалося розгадати будову багатьох білків, в тому числі гемоглобіну та інсуліну. Найбільшим досягненням комбінаторного підходу до проявів життя можна вважати розшифровку будови ДНК, зроблену в Кембриджі вченими Ф. Криком та Дж. Уотсоном у 1953 р.
Комбінаторика виявилась корисною і в хімії. Розкладуючи свій хімічний пасьянс, великий вчений Дмитро Іванович Мендєлєєв, знайшов правильне розміщення елементів, виникла таблиця – був відкритий періодичний закон.(17 лютого 1869р.). Також комбінаторика дала можливість перерахувати ізомери, котрі мають один і той самий склад, але різну будову.
У фізиці комбінаторика виявляється необхідною при вивченні властивостей кристалів, опису моделі феромагнетизму та ін..
Проекти Вільгельма Лейбніца здавалися нездійсненними тогочасним математикам, але тепер, після створення ЕОМ, багато планів Лейбніца втілюються у життя. За допомогою ЕОМ стало можливим робити перебори, що раніше потребували сотень і тисяч років.
IV. Перевірка засвоєння знань здобувачів освіти.
в) самостійна робота в парах за індивідуальними картками
Одна задача – 2 бали.
КАРТКА № 1
1. Мають 5 видів фарби. Скількома способами можна розфарбувати слово «свято», якщо всі букви повинні бути різного кольору?
2. Із цифр «1; 2; 3; 4; 5» складають числа, в яких не менше 4-х різних цифр.
Скільки таких чисел можна скласти?
КАРТКА № 2
1. Скількома способами можна розставити 7 спортсменів на 7-ми бігових доріжках?
2. В загоні 6 офіцерів і 15 рядових. Скількома способами можна сформувати загін розвідників, до якого входять 2 офіцера і 12 рядових?
КАРТКА № 3
1. Скількома способами можна розкласти 8 різних поштових листів по восьми різним конвертам?
2. Мають 12 червоних і 7 білих пронумерованих троянд. Скількома способами можна скласти букет з 5-ти троянд одного кольору?
КАРТКА № 4
1. Естафета має 4 різні за довжиною етапи. Скількома способами тренер може розподілити етапи серед 10-ти спортсменів?
2. У 6-ти дорослих та 11-ти дітей виявлено ознаки інфекційної хвороби. Щоб перевірити захворювання, треба взяти вибірковий аналіз у 2-ох дорослих та 3-х дітей. Скількома способами це можна зробити?
По закінченню роботи на екрані з’являються відповіді до всіх задач.
Учні переконуються у правильності розв’язування і перевірки та виставляють собі суму балів у відповідну колонку картки самоконтролю.
Відповіді
|
Картка №1
1.
2. |
Картка №2
1.
2.
|
|
Картка №3
1.
2.
|
Картка №4
1.
2.
|
V. Домашнє завдання
VІ. Підведення підсумків заняття.
Комп’ютерне тестування
Викладач
«ШКАЛА ОЦІНЮВАННЯ»
|
Сума балів
|
Оцінка |
|
Менше 5 балів
|
«3» |
|
6 – 8 балів
|
«4» |
|
9 – 11 балів
|
«5» |
|
12 – 14 балів
|
«6» |
|
15 – 17 балів
|
«7» |
|
18 – 20 балів
|
«8» |
|
21 – 23 балів
|
«9» |
|
24 – 26 балів
|
«10» |
|
27 – 29 балів
|
«11» |
|
Більше 30 балів
|
«12» |
в) учні отримують побажання успіху в подальшому вивченні теми: «теорія ймовірності»
Задача (додаткова) . Скількома способами можна призначити чотирьох вартових із 30 солдатів?
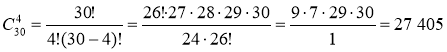 або
або ![]()


про публікацію авторської розробки
Додати розробку