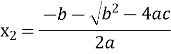Урок "Розв’язування квадратних рівнянь. Самостійна робота"

Тема.  Розв’язування квадратних рівнянь. Самостійна робота

Мета:  продовжувати формувати вміння розв’язувати квадратні рівняння; застосовувати формули коренів квадратного рівняння; розглянути спосіб розв’язування квадратних рівнянь методом виділення квадрата двочлена;

розвивати логічне та критичне мислення, пам’ять, увагу; розвивати знання учнів про рівняння;

виховувати інтерес до математики, створювати умови для розвитку творчої особистості.

Обладнання: підручник Алгебра 8 клас О. С. Істер, портрети Діофанта, Ф.Вієта; таблиці, картки для самостійної роботи.

Тип уроку: урок закріплення, знань, умінь та навичок.

ХІД УРОКУ

І. Організаційна частина

1. Привітання

2. Організація класу

3. Побажання вчителя

Невідомо хто, коли але хтось сказав слова, які передаються нам і які ми передаємо нашим нащадкам: «Намагайтесь кожного дня для кожної справи знайти якийсь позитивний початок, оскільки від того настрою, з яким ви вступаєте в день, або в якусь справу, залежать ваші успіхи, а можливо і невдачі»

Я бажаю вам розпочати урок гарним настроєм і отримати від нього задоволення і гарні результати.

ІІ. Оголошення теми і мети уроку.

Якою на вашу думку буде мета сьогоднішнього уроку?

Темою нашого уроку буде «Розв’язування квадратних рівнянь». Запишіть, будь ласка число, класна робота та тему уроку до ваших зошитів.

ІІІ. Актуалізація опорних знань

1. Математичний диктант

Назвіть перший, другий коефіцієнти і вільний член квадратного рівняння:

а) а² + 4а – 1 = 0; б) у² – 3 = 0; в) 2b² – 5b = 0; г) 3 – 2х² – х = 0; д) 3с² = 0.

2. Усний рахунок

1)

2)

3)

4)

5)

6)

3. Повторення правила

Пригадаємо, як же розв’язуються квадратні рівняння:

Учень:

Щоб рівняння розв’язати,

Треба формули всім знати,

Віднайти дискримінант – не ховайте свій талант.

Якщо тільки  D додатний,

То два розв’язки знайдем.

Якщо нуль,  шукать простіше –

На цей раз число одне.

А якщо в нас D від’ємний,

То роботі вже кінець –

Зовсім розв’язку не буде .

Зрозуміло?  Молодець!

IV. Самостійне виконання учнями під контролем і з допомогою вчителя

1. Вправа «Лови помилку»

Завдання: знайди помилку і вкажи правильну відповідь.

1.               Рівняння х²=9 має один корінь х=3.
2.               Рівняння х³-9х-1=0 квадратне і його корені …
3.               Якщо D =0, то квадратне рівняння має 2 корені.
4.               Коефіцієнти рівняння 5-3х+х²=0   а=5, в=-3, с=1
5.               Рівняння 9х²=0 не є квадратним.

2. Гра математичне «Поле чудес»

Чи знаєте ви,що квадратні рівняння вміли розв’язувати ще у Вавилоні за 2000-1700 років до нашої ери. Займалися розв’язуванням рівнянь багато вчених-математиків. Ім’я одного з них дізнаємося, коли пограємо у гру математичне «Поле чудес».

А  5х²+16=0

Д  х²=5

 І  7х²+14х=0

Н  х²=0

О  х²+4х+4=0

Т  х² - 4=0

Ф  2х²-11х+5=0

Е  х²+2х=х²+6

1. Яке рівняння можна розв’язати добуванням коренів квадратних? (Д)

2. Яке рівняння можна розв’язати способом винесення спільного множника за дужки? (І)

3. Яке рівняння можна розв’язати,представивши його ліву частину у вигляді квадрата двочлена? (О)

4. В якому рівнянні треба застосувати загальну формулу коренів квадратного рівняння? (Ф)

5. Яке з рівнянь не має розв’язків? (А)

6. Вкажіть рівняння, що має один розв’язок, який дорівнює нулю. (Н)

7. Яке рівняння можна розв’язати, застосувавши формулу різниці квадратів? (Т)

В результаті отримали ім’я ДІОФАНТ.

Ну що ж, ім’я вченого розгадали, а от рівняння залишились нерозв’язаними. Ваше завдання – самостійно розв’язати їх у зошиті.

Ця частина уроку пройде під девізом: «Математику не можна вивчити, спостерігаючи, як це робить сусід» (А. Нівен – американський математик)

(В кінці уроку потрібно буде зібрати зошити).

3. Робота з підручником

1) № 818

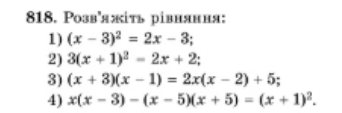
4. Самостійна робота

Самостійна  робота

ПІБ ________________________________________

V. Підсумок уроку. Випереджуюче домашнє завдання.

1. Домашнє завдання

Не можна не згадати ім’я французького математика Вієта, якого називають «батьком алгебри». Він першим почав позначати буквами не лише змінні, а й коефіцієнти. Це дало можливість узагальнити способи розв’язуваання рівнянь. Але це буде темою нашого наступного уроку. Тому самим допитливим учням ми дамо завдання: підготувати повідомлення про Франсуа Вієта та його відому теорему щодо коренів квадратного рівняння.

№819, №821

2. Підсумкове завдання

Установіть логічні пари.

А: D > 0                               1) Дійсних коренів немає

Б: D = 0                                2) Два різні корені

 В: D < 0                                3) Один корінь

Відповідь: А_________; Б_________; В__________. 

3. Оцінювання учнів

А зараз я хочу, аби ви оцінили результативність своєї роботи на уроці, використовуючи 100-бальну шкалу, зображену на дошці:

Учні оцінюють свою роботу на уроці та власні знання з даної теми. Вчитель підводить підсумки.