Урок "Теорема Вієта та теорема, обернена до теореми Вієта"
Тема. Теорема Вієта та теорема, обернена до теореми Вієта
Мета: вивчити теорему Вієта, навчити учнів застосовувати її при розв'язуванні зведених квадратних рівнянь;
розвивати логічне мислення учнів при розв'язуванні квадратних рівнянь;
виховувати інтерес до математики, увагу учнів.
Обладнання: портрет Франсуа Вієта, картки із завданнями, підручник Алгебра 8 клас О. С. Істер.
Тип уроку: комбінований
Хід уроку
І. Організація початку уроку
1. Привітання
2. Перевірка готовності до уроку
ІІ. Актуалізація опорних знань. Повідомлення теми і мети уроку
1. Перевірка домашнього завдання
Викликаю двох учнів до дошки і пропоную їм індивідуальне завдання на картках.
а) Розв’язати квадратне рівняння: х 2 - 9х + 20 = 0.
Знайти (х1 + х2 ) , (х1 х2 ).
х 2 - 9х + 20 = 0
х1 = 5 х2 =4
Відповідь: х1+ х2 = 9, х1 х2 = 20.
б) Розв’язати квадратне рівняння: 2х 2 - 5х - 3 = 0.
2х 2 - 5х - 3 = 0
D = 49 х1 = 3 х2 =![]()
Відповідь: х1 = 3, х2 =![]() .
.
2. Усне опитування
1) Як називається рівняння?
а) 5х2- 6х +1 = 0 (повне квадратне рівняння)
б) х2 - 7х + 5 = 0 (зведене квадратне рівняння)
в) 5х2 -1=0 (неповне квадратне рівняння)
2) Як називається вираз b2 - 4ас і якою буквою позначають?
(дискримінант і позначають D)
3) Скільки коренів може мати квадратне рівняння?
(два корені, якщо D > 0) (один корінь, якщо D = 0)
(нема коренів, якщо D < 0)
4) Формула коренів квадратного рівняння.
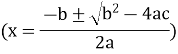
5) Яке з рівнянь зайве?
а)2х2 - х = 0;
б) х2 - 16 = 0;
в) 4х2 + х - 3 = 0;
г) 2х2 = 0; (зайве третє, бо всі неповні, а третє повне)
6) Яке з рівнянь зайве?
а) х2-5х + 1 =0;
б) 9х2-6х+ 10 = 0;
в) х2 + 2х - 2 = 0;
г) х2-3х-1 =0; (зайве друге, бо всі зведені, а друге - повне)
3. Повідомлення теми і мети уроку
На попередніх уроках ви розв'язували квадратні рівняння за допомогою дискримінанта. Зведені квадратні рівняння можна розв'язувати усно, використовуючи теорему Вієта.
Тема сьогоднішнього уроку «Теорема Вієта та теорема, обернена до теореми Вієта», яка допоможе при розв’язуванні зведених квадратних рівнянь.
ІІІ. Вивчення нового матеріалу.
Розглянемо приклад зведеного квадратного рівняння х2-9х + 20 = 0
х1 = 5 х2 =4
- Яка залежність коренів цього рівняння із коефіцієнтами?
Сума коренів дорівнює другому коефіцієнту взятому з протилежним знаком. Добуток коренів дорівнює вільному члену.
2. Доповідь про Франсуа Вієта
(Випереджаюче домашнє завдання: повідомлення учнів про Франсуа Вієта та його відому теорему щодо коренів квадратного рівняння.)
3. Доведення теореми
- Французький математики Франсуа Вієт сформулював у 1591р. теорему, яка встановлює залежність між коефіцієнтами і коренями квадратного рівняння і назвав теоремою Вієта.
Сума коренів зведеного квадратного рівняння дорівнює другому коефіцієнту, взятому з протилежним знаком, а добуток коренів дорівнює вільному члену.
Доведемо цю теорему.
Доведення
Розглянемо зведене квадратне рівняння.
x2 + px +q =0
a = 1 b = p c = q
D = p2 – 4q нехай D ![]() 0, тоді
0, тоді
x1 = ![]() x2 =
x2 = ![]()
Знайдемо суму і добуток коренів:
х1 + х2 = ![]() =
= ![]() = - p;
= - p;
х1 х2 = ![]() =
= ![]() = q;
= q;
Отже, х1 + х2 = - р, х1![]() х2 = q.
х2 = q.
4. Теорема, обернена до теореми Вієта
Використовуючи теорему Вієта, можна виразити суму і добуток коренів довільного квадратного рівняння через його коефіцієнти.
Як звести рівняння 2х2 - 5х - 3 = 0 до зведеного?
У цьому рівнянні всі коефіцієнти ділимо на 2.
Яке зведене рівняння вийде?
Х2 - ![]()
Які корені цього рівняння? Який висновок можна зробити?
х1 = 3 х2= - ![]()
х1 * х2= 3*( - ![]() ) = - 1,5
) = - 1,5
х1+ х2 = 3 + ( - ![]() ) = 2,5
) = 2,5
Справджується твердження обернене до теореми Вієта:
Якщо числа m і n такі, що їх сума дорівнює -p, а добуток дорівнює q, то ці числа є коренями рівняння x2 + px +q =0.
5. Перевірка первинного сприймання
Знайдіть суму та добуток квадратного рівняння (колективно-усно)
а) х2 -37х + 27 = 0 б) у2 + 41у - 371 = 0
х1+ х2 = 37, х1 х2 = 27 y1+ y2 = - 41, y1 y2 = - 371
в) х2 -210х = 0
х1+ х2 = 210, х1 х2 = 0 (бо вільного члена нема)
IV. Закріплення нової теми
1. Робота в парах
Знайдіть корені рівняння
а) х2 - 9х + 20 = 0
х1+ х2 = 9, х1 х2 = 20, х1 = 4, х2 = 5.
в) х2 + х - 56 = 0
х1+ х2 = - 1, х1 х2 = - 56, х1 = 7, х2 = - 8.
г) х2 - 19х + 88 = 0
х1+ х2 = 19, х1 х2 = 88, х1 = 11, х2 = 8.
2. Робота з підручником

![]()
V. Підсумок уроку
1. Підсумкова бесіда
- Чому дорівнює сума коренів зведеного квадратного рівняння?
- Чому дорівнює добуток коренів зведеного квадратного рівняння?
- Сформулюйте теорему, обернену до теореми Вієта.
2. Оцінювання учнів
3. Домашня робота
§22 №841, 846.

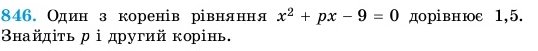
1


про публікацію авторської розробки
Додати розробку
