Урок "Розв’язування лінійних нерівностей з однією змінною"

Тема    Розв’язування лінійних нерівностей з однією змінною

Мета.

Формування компетентностей:

предметної: відтворити знання про лінійні нерівності з однією змінною; удосконалювати вміння учнів розв'язувати нерівності  з однією змінною, формувати навички самостійної роботи

ключові – інформаційно-цифрової; соціальної і громадянської; спілкування державною мовою, уміння вчитися впродовж життя.

Тип уроку:  формування вмінь і навичок

 Обладнання: ноутбук, презентація

                                        Епіграф: «Не достатньо мати  лише добрий розум, 

головне — це раціонально застосовувати  його».

Рене Декарт

Хід уроку

І. Організаційний момент.

     1) Привітання

      2) Перевірка присутніх

ІІ. Тема

Тема уроку:                  Розв’язування лінійних нерівностей з однією змінною

Мета:

Епіграф уроку:

ІІІ.  Актуалізація опорних знань

1)«Бліц-інтерв’ю»

1.              Що  таке нерівність?
2.              На які види поділяються нерівності в залежності від знака?
3.              Що називають  розв’язком нерівності?
4.              Що  означає розв’язати нерівність?
5.              Чим відрізняються розв'язки нерівностей     х ≤ 4    та    х < 4   ?
6.              Чим відрізняються проміжки   [-3; 4]   та (-3; 4)?

2) Тест “Бліц-опитування”  “ТАК”-1, “НІ”- 0

1.    Чи є число 4 розв’язком нерівності 2х<10?
2.    Чи є число -2 розв’язком нерівності 5х>- 3?
3.    Чи є нерівність 2х+6<7х-4 строгою?
4.    Чи існує ціле число, яке належить проміжку [-5,8; -5,6]?
5.    Чи правильно, що при діленні обох частин нерівності на додатнє число знак нерівності  не змінюється?
6.     Чи правильно, що при діленні обох частин нерівності на від’ємне число знак нерівності не змінюється на протилежний?

                      Відповідь:    101010

3) Поставити у відповідність кожній із нерівностей проміжок

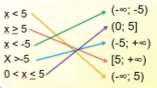
4) За даними проміжками запишіть нерівності, яким вони відповідають

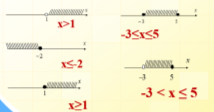
5) Кросворд «Хто вперше ввів знаки нерівностей <,  >?»

Історична довідка

Символи  ≥,  ≤  (нестрогі знаки нерівності) введені в 1734 році французьким математиком П'єром Бузі.

ІV. Розвязування вправ

1. колективно

2. робота з підручником

          № 28.6(4, 6), 28.18(2), 28.20, 28.22

V. Самостійна робота

VІ.  Підсумок  уроку.

                         Говорячи про нерівність, як про математичне поняття, хочеться внести до нашого уроку деякого різномаїття і тим самим заперечити той факт, що математика суха та нудна наука. Поєднати  і порівняти на перший погляд   різні предмети, наприклад алгебру та літературу. Послухайте як почуває себе «нерівність» в поезії.

Нерівність душ

Нерівність душ страшніша всіх розлук,

Нерівність душ-це бачиш різне сонце.

Але не відчуваєш його рук,

Хоч дивишся завжди в одне віконце.

Нерівність душ-це гірше,ніж тримать

В руках якесь розпечене залізо.

Нерівність душ потрібно признавать

Тоді,коли іще не буде пізно.

Нерівність душ-це різніі світи,

Це різне небо,навіть різні хмари.

Молю, цим свою душу не топчи,

І відпусти примарливі лиш чари... 

 Віда Вансель

А за активну участь на уроці та  

    розвязування математичних нерівностей

     оцінки…

VІІІ. Домашнє  завдання

П.28 повторити

№ 28.15,   28.17(2,4),   28.19(2),   28.21

за підручником  А.Г.Мерзляк, В.Б.Полонський, М.С.Якір для 8 класу: Алгебра для загальноосвітніх навчальних закладів з поглибленим вивченням математики:– Х.: Гімназія, 2016