Урок "Розв'язування нерівностей з двома змінними"

Про матеріал

Урок "Розв'язування нерівностей з двома змінними" .Алгебра, 9 клас з поглибленим вивченням математики. При побудові графіків можна використати програму Gran1W.

Перегляд файлу

9Б клас

Вчитель Шаповалова Л.В. ХЛ№161 « Імпульс» місто Харків.

Тема: Нерівності з двома змінними.

Графік нерівності з двома змінними.

Мета: Забезпечити засвоєння учнями поняття нерівності з двома змінними та її розв’язків, графічного зображення розв’язків.

Формувати навики побудови графіків нерівності з двома змінними, застосування контрольних точок.

Розвивати логічне мислення учнів.

Виховувати інтерес до вивчення математики, потяг до наукової творчості. Виховувати охайність, відчуття задоволення від розв’язування завдань підвищеної складності.

Тип уроку: комбінований.

Обладнання: комп’ютери класу з прикладною програмою Gran1W.

Хід уроку.

І Мотивація. Ви умієте знаходити розв’язки нерівностей з однією змінною, та зобразити їх на координатній прямій:

3х-2>0; х²-7х+12≤0; (х-3)(х+6)(х-5)≥0; ; х²≥0; х²+1<0.

Що буде розв’язком нерівності, яка містить дві змінні?

Наприклад 2x-y>1 або y>x² .

Учні висловлюють свої припущення.

Сьогодні на уроці відповімо на це запитання та розглянемо приклади нерівностей з двома змінними та їх розв’язки.

Наприклад такі: 2x-y>1; у<2х-х² ; ху≤6; х ²+2х+у²≥3; (х-у)(х+у-1)>0 ; х²–у²≤0.

Перевіримо побудову графіків Д/З.

І. Актуалізація опорних знань. Перевірка Д/З.

(Побудувати графіки функцій 2x-y=1; у=2х-х²; ху=6 ;

та рівнянь: х ²+2х+у²=3;

(х-у)(х+у-1)=0 ;

х²–у²=0.

Побудову виконати в зошитах та на ПК.)

Учні демонструють графіки функцій та рівнянь на ПК, перевіряють побудову в зошитах. 6 учнів виконують ці завдання на дошці. Учні класу на полях зошитів ставлять відмітку +; - ; ± в залежності від правильності виконання завдання.

ІІ. Формування знань.

Нерівність 2x-y>1, є нерівністю з двома змінними. Впорядковану пару чисел, яка перетворює нерівність з двома змінними у правильну числову нерівність, називають її розв’язком.

Наведіть приклади пари чисел, які є розв’язком даної нерівності. Скільки існує таких пар?

Розв’язати нерівність з двома змінними – це означає знайти множину її розв’язків.

Знаходження цієї множини для нерівностей з двома змінними становить певні труднощі. Тому зручно користуватися геометричним методом, бо за допомогою нього її можна наочно зобразити.

Чи є пара чисел (2;5), (2:-3) ,(4;1),((-2;-1), (2;3) розв’язком даної нерівності? Перевірте, підставивши їх координати у нерівність.

Відмітьте ці точки на координатній площині, де побудовано графік рівняння 2x-y=1, тобто у=2х-1.

Де розташовані точки, координати яких є розв’язком нерівності? І де ті, які не є розв’язком нерівності?

Зробіть висновок.

( Учні висловлюють свої припущення)

Розв’язки нерівності з двома змінними задають певну множину точок на координатній площині, яку визначають за допомогою рівняння, що отримується з даної нерівності заміною її знака на знак рівності. Встановлення цієї множини і становить суть геометричного (графічного) способу розв’язування нерівності з двома змінними.

Точки графіка одержаного рівняння будуть належати множині розв’язків даної нерівності тільки тоді, коли вона нестрога. У цьому разі на координатній площині графік рівняння зображується суцільною лінією, в другому – пунктирною.

Пропоную учням сформулювати алгоритм розв’язування нерівності.

Висновок:

геометричний спосіб розв’язування нерівності на прикладі нерівності першого степеня з двома змінними

будуємо графік відповідного рівняння: у=2х-1.

Це рівняння у=2х-1визначає на координатній площині пряму, яка ділить площину на дві півплощини: півплощину (І), розміщену вище від прямої, і півплощину (II), розміщену нижче, від прямої

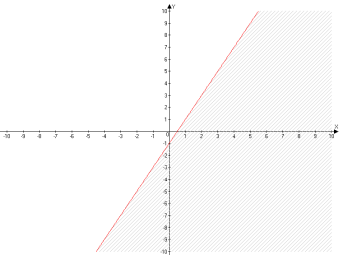
Геометрично множина всіх розв’язків нерівності у<2х-1 зобразиться множиною точок півплощини (І), а нерівності у>2х-1– множиною точок півплощини (II).

Кажуть також, що нерівність у<2х-1визначає півплощину (І), а нерівність у>2х-1 – півплощину (II).

(Демонстрація на ПК)

Завдання учням. Зобразіть графік нерівності , (у<2х-1) на площині де побудовано графік у=2х-1.

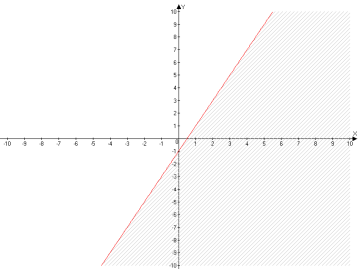
IІІ. Удосконалення вмінь і навичок.

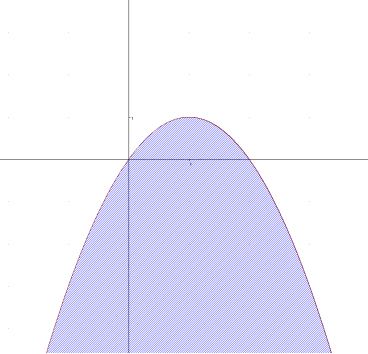
Побудувати графік нерівності у<2х-х²та

ху≤6 ; х ²+2х+у²≥3; (х-у)(х+у-1)>0 ; х²–у²≤0.

Учні пропонують застосувати графіки, які вони побудували дома.

Яка ж площина є розв’язком?

Учні пропонують методи встановлення відповідної площини.

Висновок. Формулюється метод застосування контрольної точки.

Звертаю увагу на строгі та нестрогі нерівності.

Побудова графіків у зошиті з наступною перевіркою на комп’ютері.

5 учнів по черзі виходять до дошки, на готових графіках виділяють частину площини , яка є розв’язком нерівності. Пояснюють визначення відповідної площини застосуванням контрольної точки.

у<2х-х²

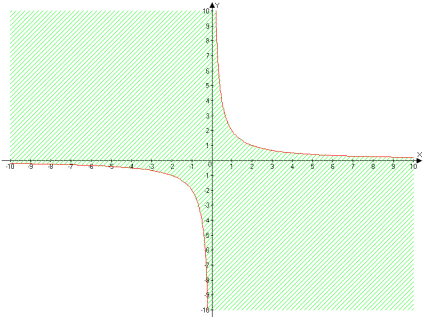
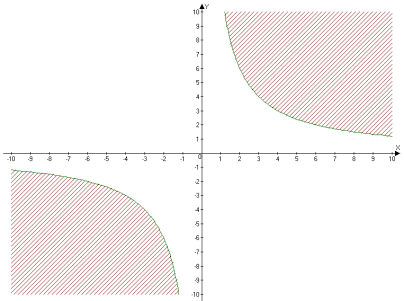
ху≤6 (у≤

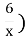
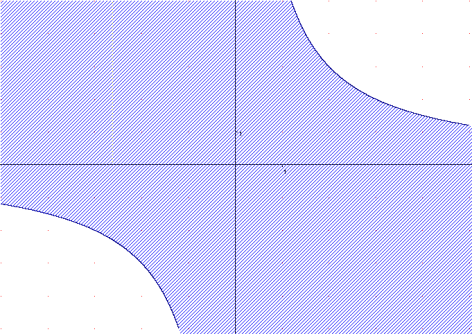
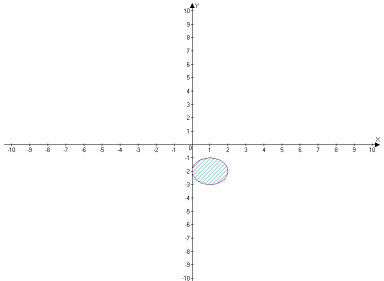
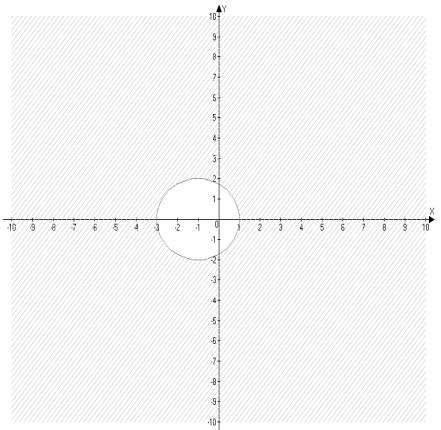
х ²+2х+у²≥3, (х-1)²+у²≥4

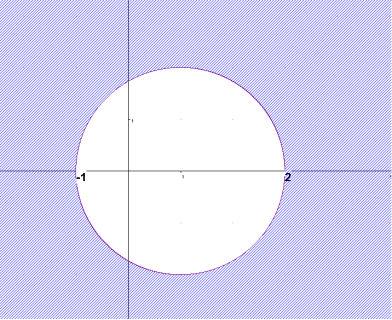
(х-у)(х+у-1)>0

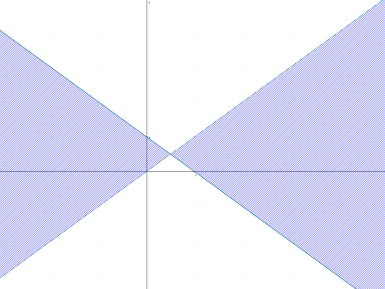
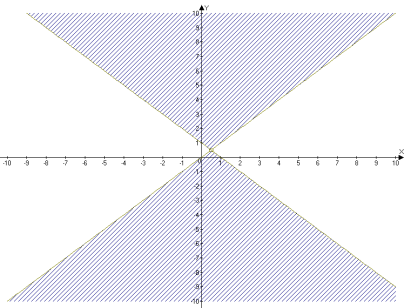
х²–у²≤0.

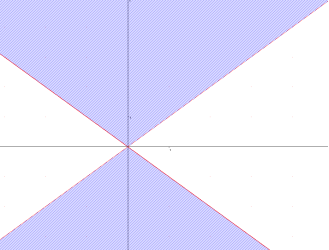
Які розв’язки нерівностей: а) у<-1, (0х+у?

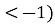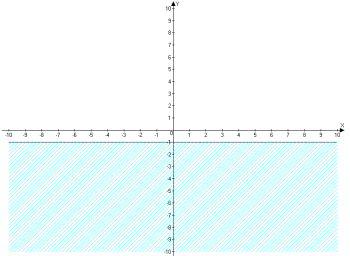
б) , (х+0у3).

( Демонстрація на ПК)

Самостійна робота

Побудувати графік нерівності:

І варіант

у< (9 балів)

ІІ варіант

(9 балів)

ІІІ* варіант

(12 балів)

ІV* варіант

(12 балів).

Перевірка самостійної роботи з використанням ПК.

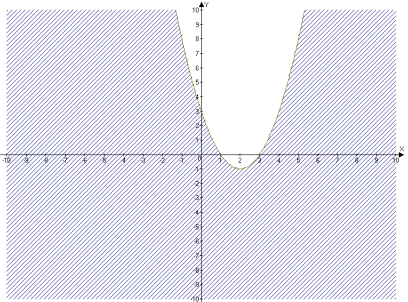
1 варіант

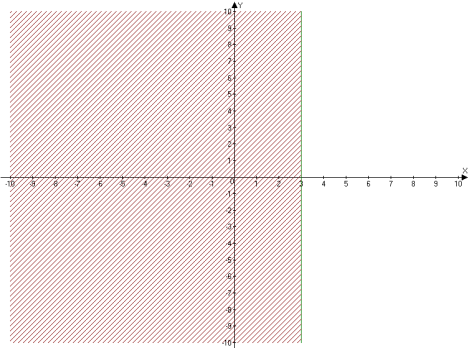
у<

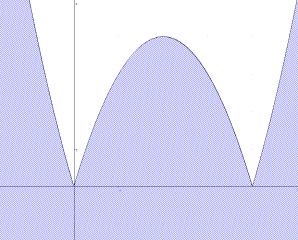
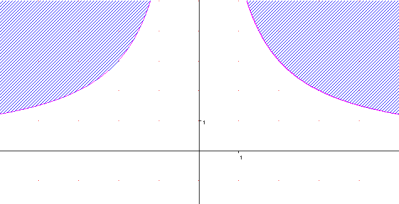
2 варіант

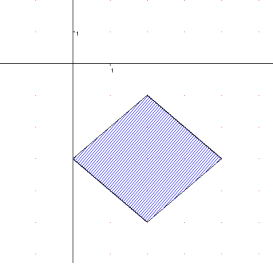
3 варіант

(²+(²>0.

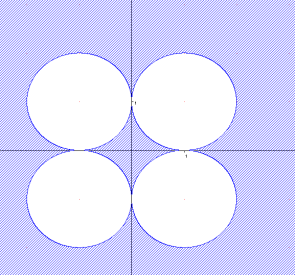
4 варіант

(

IV. Підведення підсумків уроку.

Що є розв’язком нерівності з двома невідомими?
Що є графіком нерівності з двома невідомими?
Який алгоритм побудови графіка нерівностей з двома змінними?
Оцінка за урок (учні виставляють собі в зошит +;-;± та одержані оцінки) :

Д/З -

Відповідь біля дошки –

Усні відповіді на уроці –

Самостійна робота -

САМООЦІНКА ( Як я засвоїв (засвоїла) матеріал уроку) -

V. Перспектива. Розв’язування нерівностей, які містять множники постійного знаку х²(у-х²)>0 , розв’язування завдань з параметрами в системі хоа та систем нерівностей з двома невідомими.

VІ. Домашнє завдання.

Вивчити п.19. Завдання №19.15(1,2,5,6*,7*).