Урок: "Розв’язування прикладних задач з теми «Тіла обертання»"

 

 

 

 

Тема заняття: Розв’язування  прикладних  задач

Мета заняття:

навчальна:

     узагальнити знання студентів про тіла обертання, їх об′єми та площі поверхонь; 

     формувати    вміння студентів застосовувати формули об′єму та    площі

      повної поверхні тіл обертання до розв’язування задач;

розвиваюча:

     розвивати самостійність мислення, інтелектуальні та творчі здібності,

     чіткість та логіку мислення;

виховна:

     виховувати активність, наполегливість, працьовитість; розширювати

     кругозір студентів та їхню просторову уяву; вчити орієнтуватися   в

     нестандартних ситуаціях.

Тип заняття: заняття узагальнення та систематизації знань, умінь і навичок

 

Хід заняття:

І. Організаційний момент.

ІІ. Мотивація навчальної діяльності.

       Шановні студенти! Знаю, що ви мрієте стати високо­кваліфікованими спеціалістами, добре володіти усіма нюансами своєї майбутньої професії, мрієте  також бути гарними господарями. У цьому вам допоможе математика. Математичні знання потрібні в повсякденному житті, а також  для за­своєння курсів фізики, економіки, загальнотехнічних і спеці­альних дисциплін. На заняттях з геометрії вам, майбутнім перевізникам, особ­ливу увагу слід приділити вивченню теми «Тіла обер­тання». Адже форму циліндра, кулі, конуса чи зрізаного конуса мають багато деталей і вузлів машин та ме­ханізмів. Тому в житті і професійній діяльності ви, безперечно, матимете справу з  такими геометричними тілами.

Ми закінчуємо вивчення теми «Тіла обертання». Тому сьогодні маємо повторити та узагальнити матеріал із даної теми, здобути вміння впроваджувати теорію на практиці під час розв’язування задач та в практичній діяльності.

 

 

ІІІ. Формування мети і завдань заняття.

Вступне слово викладача

Наше заняття пройде у нестандартній формі – захисту власних проектів. Ми з вами поділилися на групи: теоретики, історики, практики, і в залежності від обраної категорії - групи виконували завдання з отриманих буклетів про проект «Тіла обертання навколо нас».

 Всі ви готувалися до сьогоднішнього заняття, тому прагнете отримати високу оцінку. Пропоную вам влаштувати  індивідуальні змагання. На кожному етапі заняття потрібно буде виконати те чи інше завдання, яке оцінюється певною кількістю балів. Таким чином, в кінці заняття кожен з вас володітиме деякою кількістю балів, які переведемо в оціночні за принципом ЗНО (тобто, щоб отримати 4 потрібно набрати 6 балів, найбільша кількість балів – оцінка 12, решта оцінок – пропорційно кількості балів). Результати будуть заноситись у таблицю, яку ви бачите на дошці. 

 

IV. Узагальнення та систематизація знань

 І група – ТЕОРЕТИКИ

 Завдання: зібрати основні відомості про тіла обертання: циліндр, конус, куля, сфера, складові елементи, та все це скласти в презентацію та  інформаційну картку.

 Виступ групи «Теоретики»

І студент

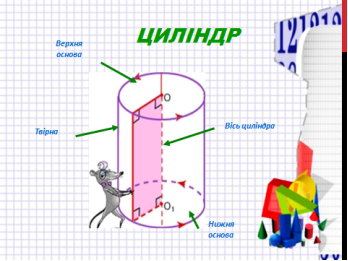
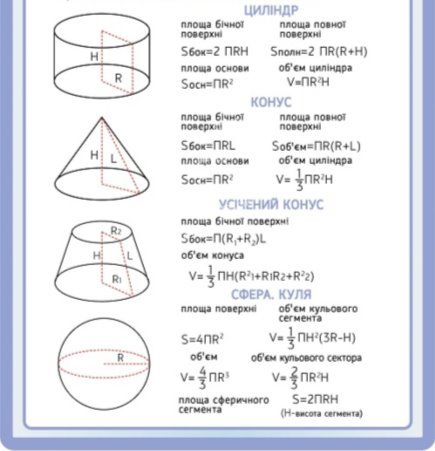
   Циліндром називається тіло, утворене обертанням прямокутника навколо його сторони. Якщо прямокутник обертати навколо однієї  із сторін, то його  суміжні сторони опишуть рівні круги, які називають основами циліндра. Паралельна сторона опише бічну поверхню циліндра. Кожен відрізок цієї поверхні, який з’єднує основи називається твірною циліндра. Усі твірні циліндра рівні та паралельні одна одній,  кожна з них паралельна  і рівна осі обертання. Довжина твірної є висотою циліндра.

 Усі осьові перерізи циліндра – рівні прямокутники. Усі осьові перерізи циліндра – рівні прямокутники. Кожна січна площина, паралельна осі циліндра, перетинає його по прямокутнику. Кожна січна площина, перпендикулярна до осі циліндра, перетинає його по кругу, що дорівнює основі циліндра.

Формули

• S_б=2πRH – площа бічної поверхні,
• S_п=2πR(R+H) – площа повної  поверхні,
• V =2πRH - об’єм.

 

ІІ студент

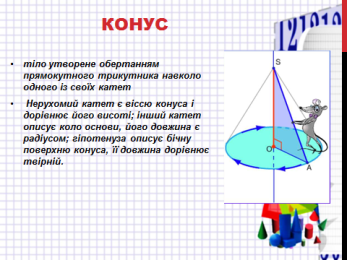
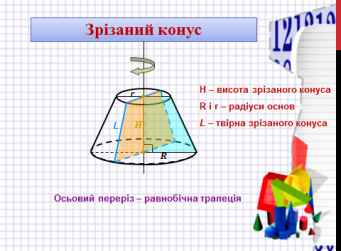
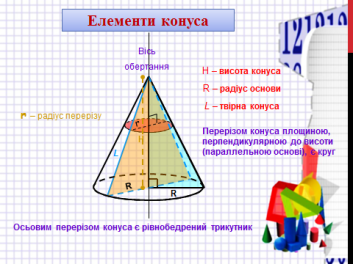
     Конусом називається тіло, утворене обертанням прямокутного трикутника навколо його катета. Якщо прямокутний трикутник обертати навколо одного з катетів, то його гіпотеза опише бічну поверхню, а інший катет основу конуса. Точка S вершина конуса, SО – висота конуса та вісь конуса.

       Усі осьові перерізи конуса – рівні рівнобедрені трикутники. Кожна площина, яка проходить через вісь конуса, є площиною його симетрії. Центра симетрії конус не має. Відрізок, який сполучає вершину конуса з будь-якою точкою кола його основи, називають твірною конуса. Усі твірні конуса рівні.

Формули

• L²=H²+R² – довжина твірної.
• S_б=πRL – площа бічної поверхні.
• S_п=πR(R+L) – площа всієї фігури.
• V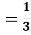πR²H – об’єм фігури.

 

ІІІ студент

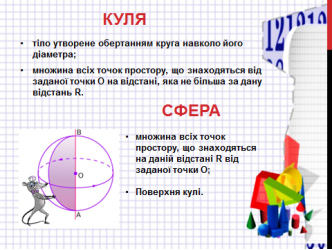
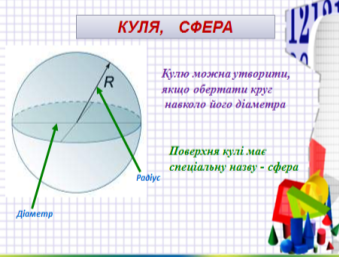
    Кулею називається тіло, утворене обертанням круга навколо його діаметра. Центр круга, обертанням якого утворено кулю, називають центром цієї кулі. Відрізок, який сполучає дві точки поверхні кулі та проходить через її центр, - діаметр кулі.

Кожна площина, яка проходить через центр кулі, поділяє її на дві рівні півкулі і є площиною симетрії кулі. Вона перетинає кулю по великому кругу, а поверхню кулі – по колу великого круга.

Сфера – це поверхня кулі. Перерізом сфери є коло

 

Формули

• S_осн=πR² – площа великого круга;
• D=2R – діаметр кулі;
• S=4πR² – площа сфери;
• V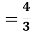πR² – об’єм кулі.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

	Варіант 1				Варіант 2
1. Закінчіть речення: „Тіло, утворене обертанням прямокутника навколо однієї зі своїх сторін називається…”		1     2                   5         6       7       8 9	1. Закінчіть речення „Твірна циліндра є його…”
2. Скільки основ має циліндр?			2. Що є розгорткою бічної поверхні циліндра?
3. Закінчіть речення: „ Осьовим перерізом циліндра є…”			3. Закінчіть речення:„ Перерізом циліндра площиною, паралельною його основі, є…”
4.  Запишіть формулу, за якою обчислюється площа повної поверхні циліндра.			4.Запишіть формулу, за якою обчислюється об’єм циліндра
5. Скільки твірних у конуса?			5. Скільки основ має конус?
6. Якщо висота конуса дорівнює 3 см, а радіус основи – 4 см, то його твірна дорівнює…			6. Якщо твірна конуса дорівнює 5 см, а висота – 4 см, то радіус його основи дорівнює…
7. Запишіть формулу, за якою обчислюється об’єм конуса.			7. Запишіть формулу, за якою обчислюється площа бічної поверхні конуса.
8.  У конусі діаметр основи дорівнює 16 см, а твірна – 10 см. Знайдіть об’єм цього конуса.			8.  Знайдіть об’єм конуса, якщо діаметр його основи дорівнює 12 см, а твірна – 10 см
9.  Як називається хорда, яка проходить через центр сфери?			9.  Закінчіть речення: „Будь-який переріз кулі площиною є…”
10.  За якою формулою обчислюється об’єм кулі			10.  За якою формулою обчислюється площа сфери?
11. Знайти довжину великого кола сфери, діаметр якої дорівнює 18 см.			11. Діаметр кулі дорівнює 6 см. Знайти площу великого круга кулі.
12.Діаметр кулі дорівнює 6 см. Знайти площу поверхні кулі.			12.Знайдіть об’єм кулі, якщо довжина радіуса 3см.

Математичний диктант з теми „ Тіла обертання”

Відповіді

 

№ 1

№ 2

№ 3

№ 4

№ 5

№ 6

№ 7

№ 8

№ 9

№10

№11

№12

І в

циліндр

дві

Прямо кутник

2πRH+ +2πR2

безліч

5см

π R2H

128π см3

діаметр

πR3

18π см

6π см3

ІІ в

висотою

Прямо кутник

Круг

π R2H

дві

3см

πRl

96π см3

кругом

πR2

36π см2

36π см3

 

 

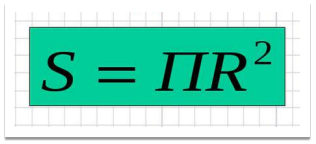
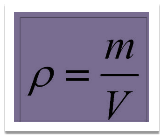Інформаційна картка

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ІІ група – ІСТОРИКИ

Завдання: з’ясувати історію походження термінів та понять, пов’язаних з тілами обертання. За даними матеріалами підготувати презентацію та гру «Вірю не вірю».

1-й історик

        Початкові відомості про властивості геометричних тіл,зокрема, тіл обертання люди  здобули, спостерігаючи навколишній світ і в результаті  власної практичної діяльності.

До Фалеса в світі геометрією майже ніхто не займався. У геометричних фігур не було назв. Тому люди почали вигадувати їм свої назви.

       Ялинкова шишка з грецької означає слово "конос", тому тіла такої форми отримали назву конус. Перші згадки про конус, як геометричне тіло перейшли до нас від греків. За період з VII по III століття до нашої ери грецькі геометри збагатили геометрію численними новими теоремами, зробили серйозні кроки до суворого її обгрунтування.

          Багатовікова робота грецьких вчених  була підсумована Евклідом (325 до н. е.—  265 до н. е.) в його знаменитій праці «Начала». В XI книзі дається таке визначення конусу: якщо прямокутний трикутник обертається близько одного зі своїх катетів зліва і повернеться в той же самий стан, з якого він почав рухатися, то описана фігура буде конусом.

   Евклід розглядає тільки прямі конуси, тобто такі, у яких вісь перпендикулярна до основи, лише Аполлоній(262 до н. е. —  190 до н. е.) розрізняє прямі і косі конуси, у яких вісь утворює з основою кут, відмінний від прямого.

   У XII книзі «Начала» Евкліда  містяться наступні теореми.

•  Об'єм конуса дорівнює однієї третини об'єма циліндра з рівною основою і рівною висотою; доведення цієї теореми належить Евдоксу Книдському (408 до н. е. —  355 до н. е.) .
• Відношення об'ємів двох конусів з рівними основами дорівнює  відношенню відповідних висот.
• Якщо два конуса рівновеликі, то площі їх основ обернено пропорційні відповідним висотам і навпаки.

   Безпосереднє обчислення об'єму конуса дає Герон Олександрійський         (I століття н. е.). Бічна поверхня конуса, як і циліндра, була знайдена Архімедом (287 до н. е. — 212 до н. е.). Про неї говориться в книзі «Про кулі і циліндри».                                                                                                 

  2-й історик 

       Слова «куля» і «сфера» походять від одного і того ж грецького слова «сфайра» - м'яч.

      У давнину сфера була у великій пошані. Астрономічні спостереження над небесним склепінням  неодмінно викликали образ сфери. Піфагорійці вчили про існування десяти сфер Всесвіту, за якими нібито рухаються небесні тіла. Вони стверджували, що відстані цих тіл один від одного пропорційні інтервалам музичної гами. У цьому вбачали елементи світової гармонії. У подібних напівмістичних міркуваннях полягала піфагорова «музика сфер».

      Аристотель (384до н. е.-322 до н. е.) вважав, що кульова форма, як найбільш досконала, характерна для Місяця, Сонця, Землі і всім світовим тілам.

    У ХI книзі «Начал» Евклід ( 325 до н.е.- 265  до н. е.) визначає кулю як фігуру, яка утворюється при обертанні півкруга навколо його нерухомого діаметра. Він довів тільки теорему про те, що об'єми двох куль відносяться як куби їх радіусів, але не виводить формули і не дає ніякого правила, якого напевно, і не знав для обчислення площі поверхні сфери та об'єму кулі.

Виведення формул об'єму кулі і площі поверхні сфери - одне з найбільших відкриттів Архімеда (287 до н. е.- 212  до н. е.).

   У його творі «Про кулі і циліндри» є  теореми  про площу поверхні сфери та об’єм кулі:

• Площа поверхні сфери дорівнює  збільшеної  учетверо площі її великого круга.
•  Об'єм кулі дорівнює збільшеному в чотири рази об'єму конуса, основою якого служить великий круг, а висотою - радіус кулі.

 

   3-й історик

  Слово циліндр походить від грецького слова κύλινδρος , що означає "вал", "каток". З циліндром люди знайомі з глибокої давнини.

        Циліндр з вписаною кулею – символ одного з прекрасніших відкриттів Архімеда – був зображений на його надгробному камені в Сіракузах.

        В 1906 році була виявлена книга Архімеда (287-212 рр. до н. е. ) "Про метод", у ній розглядається розв'язання задачі про об'єм  спільної частини циліндрів, які перетинаються. Архімед приписує частину відкриття цього принципу – Демокріту (470-380 р. до н. е. ) – давньогрецькому філософу - матеріалісту. Саме Демокріт одержав формулу для обчислення об'єму піраміди і конуса.
   Багато зробила для геометрії школа Платона. Платон (428-348 рр. до н. е.) був учнем Сократа (470-399 рр. до н. е.). Цій школі належить:

 

• дослідження властивостей призми, піраміди, циліндра та конуса;
•  вивчення конічних перерізів.

 

        Великий трактат про конічні перерізи був написаний Аполлонієм Пергським (262-190 рр. до н. е.) – учнем Евкліда (III ст. до н. е..). Це його вважають автором  великої  праці з 15 книг під назвою "Начала". Ці книги видаються і до цього часу, а в школах Англії за ними навчаються досі.

 

4-й історик:

      Циліндри Фараона - таємниця тисячоліть.

      У деяких статуй, залишених нам давньоєгипетською культурою, ми можемо побачити затиснуті в руках предмети циліндричної форми, наприклад, в скульптурній групі, що зображає фараона Менкаура в оточенні богині Хатор і богині Ному.

         Десь на початку 1976 року, дослідники В. Ковтун та Р. Добровольський, на території Закавказзя виявили дуже стародавній рукопис під назвою «Таємниці Життя і Смерті». У ньому мова йде про Сонячні і Місячні циліндри, виготовлені з міді та цинку, а також з особливого внутрішнього наповнення. Згідно з твердженнями невідомого автора, ці загадкові для нашого розуму циліндри, колись використовувалися великими жерцями і фараонами Стародавнього Єгипту для спілкування з богами і зміцнення життєвих сил.

       Завдяки одному старовинному рецепту, який дійшов у рукописах до наших часів, Циліндри Фараона були відтворені, а потім вивчалися відомим фізиком Володимиром Ковтуном. В дослідженнях брали участь провідні єгиптологи, медики, парапсихологи і екстрасенси.

         Отримані результати дослідження дуже вразили вчених. З’ясувалося, що Циліндри Фараона володіють дивовижними властивостями, які можуть впливати на організм людини. Багато сучасних медиків вважають, що Циліндри Фараона – це унікальний, фізіотерапевтичний прилад, створений якимось генієм Стародавнього Єгипту. Вони здатні захищати від впливу випромінювань різних електронних пристроїв – мікрохвильових печей, телевізорів, персональних комп’ютерів і т.д. Це вже неодноразово було доведено дослідженнями та експериментами.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ГРА «ВІРЮ – НЕ ВІРЮ»

1. Чи вірно, що книгу «Начала» написав Архімед? [Ні,Евклід]
2. Чи вірно, що назви тіл обертання походять з Древнього Єгипту? [Ні, це слова грецького походження]
3. Чи віриш ти, що Шарль Перро, автор «Червоної шапочки», написав казку «Кохання циркуля та лінійки»?  [Так, є така казка]

4. Чи віриш ти, що брати Грімм написали казку «Дивовижні пригоди     трикутника»? [Ні]

5. Чи віриш ти, що Лев Толстой був автором підручника з математики?

[Так, він написав підручник для початкової школи]

6. Чи віриш ти, що до сьогоднішнього дня в школах Англії досі вчаться за книгами Аполонія Пергського? [Так]

7. Чи віриш ти, що О.С.Пушкін написав такі рядки: «Натхнення необхідне в геометрії, як і в поезії»? [Так]

8. Чи віриш ти, що великий Евклід сказав царю Птоломею, що в геометрії немає царської дороги? [Так]

9.Чи вірно,що виведення формул об’єму кулі та площі поверхні сфери – одне з найбільших відкриттів Архімеда?  [Так]

10. Чи віриш ти, що школа Платона проіснувала тисячу років? [Так]

11. Чи віриш ти, Аристотель вивів формулу об’єму конуса? [Ні]

12. Чи віриш ти, що сьогодні можна купити циліндри фараона? [Так]

 

Ключ до гри

№ 1	№ 2	№ 3	№ 4	№ 5	№ 6	№ 7	№ 8	№ 9	№10	№11	№12
-	-	+	-	+	+	+	+	+	+	-	+

 

Виступ груп – ПРАКТИКИ

 Завдання: з’ясувати де зустрічаються тіла обертання в повсякденному житті, скласти задачі з прикладним та професійним змістом на застосування тіл обертання.

 

Група 1 -  «Тіла обертання в повсякденному житті»

І студент

        Підчас  вивчення теми "Тіла обертання" , коли  отрямали завдання я почала спостерігати які ж саме предмети навколо мене можна віднести до циліндричної, конічної, кульової форми. Зайшла  на кухню поснідати і ось: стакан, чашка, тарілка, чайник, лійка, плафон, що висить на стіні, всі ці предмети можна віднести до цих форм. Їх - безліч. То ж ми вирішили, що роботу над проектом проведемо тут  - на кухні.

     Кухня –це жіноча територія і, щоб бути на ній господинею потрібно знати все про те, що тут відбувається. Почнемо з інвентарю. Майже весь посуд – це циліндри. Таку форму мають: каструлі, кружки, склянки, форми для випічки, солонки, банки для спецій, тощо… Їжа теж має таку форму циліндрів. Згадайте: сир, колбаса, піцца, суші… А солодощі… Ці  циліндри не тільки смачні, а й гарні.

 

ІІ студент

     Конусів  на кухні меньше, ніж циліндрів, але без них не обійдеться жодна господиня. Швидко щось перелити(лійка), прекрасити тортик(кулінарний шприц), чи оригінально  подати напій. Тут допоможуть конуси.

 Потрібно відмітити, що багато овочів мають таку форму: морква, редис, кукурудза,перець… А солодощі у формі конуса стануть вишуканою прекрасою будь-якого столу.

    Форму кулі мають багато фруктів, цитрусових, ягід. Цукерки, морозиво, пампушки –все це педмети круглої форми.

Я думаю, ми вас переконали, що тіл обертання на кухні багато. Звичайно, приготувати смачні страви без знання формул з геометрії- можливо, але щоб  бути гарною господинею необхобідно вміти правильно порахувати пропорції, об’єми, площі. Переконайтеся у цьому, розв’язавши наші задачі.

 

ІІІ студент

Задача 1

На вечірку прийде 20 людей, для кожного з них потрібно приготувати по 1 бокалу соку. Висота фужеру 12 см, а діаметр 10 см. Скільки літрових пачок соку потрібно закупити для вечірки.

Задача 2

Морозиво «Каприз»: висота стаканчика 7 см, діаметр стаканчика - 5см, радіус півкульки – 6 см. Знайти об’єм морозива.

Задача 3

Скільки напівкруглих тістечок поміститься на конусі з твірною 26 см і радіусом основи 10 см. Якщо радіус тістечка 2 см. Втрати на заповнення – 20%.

Час розв’язування задач – 5 хвилин.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Група 2 -  «Тіла обертання в господарстві»

І студент

Ми  також будемо розповідати про тіла обертання у побуті,але з чоловічої точки зору. Знання геометрії допоможуть нам стати справжніми господарями.

Тіла обертання в побуті зустрічаються дуже часто. Почнемо свою розповідь з конусів.  Форму конусів  та зрізаних конусів мають плафони світильників, свердла, відра, тазики, ролики багатьох підшипників  дахи будівель  деталі побутових машин  лійки і т.д.

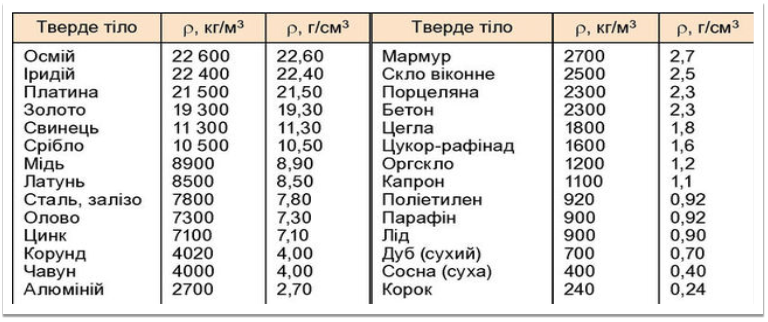
Сипучі матеріали в природі часто також набувають форми конуса. Але, що цікаво, ці конуси завжди мають цілком певний кут нахилу твірної до площини Землі — так званий кут природного укосу. При цьому кожному сипучому матеріалу відповідає певний кут природного на­хилу. Так, наприклад, піску відповідає кут нахилу в 25°, глині -30°, щебеню - ЗЗ°, вугілля - 42 °. Для картоплі він 45°, вугілля — 42°, ґрунту — 40°, глини -30°, піску — 25°.

 Окрім того, в житті користуються не довжиною твірної, а довжиною перекиду (двох твірних), який виміряти значно легше.

 

Ще одним поширеним конусом  є  пожежні відра. Їх роблять у вигляді конусів тому що, такими відрами зручніше черпати пісок з пожежного ящика (адже, вогонь гасять не тільки водою, але і піском).

Щоб зачерпнути пісок, треба взятися однією рукою за дужку відра, а іншою - за його дно. З плоского днища звичайного відра рука в громіздкій пожежній рукавиці зісковзує. Набагато зручніше триматися за кінець конуса. До того ж конусоподібне відро легше занурювати в пожежну бочку з водою і виймати з неї вже наповненим.
      Крім того, взимку вода в бочці може перетворитись на лід. Кінчиком конуса пробити його легше. Пожежники також стверджують, що з відра-конуса воду можна виплеснути далі і точніше, ніж зі звичайного. Також форму конуса мають наконечники пожежних рукавів. Можна зробити висновок , що багато конусних форм використовуються для  збільшення  тиску, та точності.

 

ІІ студент

Циліндрів у побуті та техніці дуже багато: труби, проводи , бочки, свердловини, колодязі, валики, камери , тощо.

Прикладом циліндрів є:

1) Цистерни

    Цистерна (лат. cisterna - коробка) це резервуар для рідин, у першу чергу   для  води, нафтопродуктів, розчинів хімічних речовин, сипких речовин тощо. Зараз в інтернеті існує багато онлайн-калькуляторів об’єму  рідини в цистерні , та ці калькулятори не завжди доступні, тому знайти  все можна за допомогою формул.

2)Труби:

В наш час труби зу­стрічаються дуже часто. В кожному міському домі різних труб сотні метрів - во­допровідні, опалювальні, газові, каналізаційні, водостічні, вентиляційні. На хімі­чних і металургійних заводах їх сотні кілометрів, а гігантські магістральні газо та  нафтопроводи прокладають на багато тисяч кілометрів.

 

ІІІ студент

          Кожного дня ви маєте потребу використовувати речі форми кулі чи сфери. Ось наочні приклади, лише деяких видів куль та сфер: м’ячі для багатьох видів спорту, аеростати, кульки для підшипників, плафони, цукерки, дитячі іграшки, овочі та фрукти.

       Невипадково піфагорійці вважали кулю найвишуканішою просторовою фігурою.

  Найпростіша деталь багатьох механізмів – підшипник – має також кульову форму, яка дуже поширена в техніці І це не випадково, бо саме куля зазнає найменшого тертя під час роботи підшипників.

       Серед тіл, що мають задану площу поверхні, куля має найбільший об’єм.

Задача 1

Купа щебеню має конічну форму, радіус основи якої, 2м і твірна 3,5м. Скільки треба машин, щоб перевести щебінь складених в 10 таких купах?

                   Маса 1 щебеню дорівнює 3т.   Вантажопід'ємність машини – 5т.

 

 

Задача 2

Циліндрична димова труба діаметром 65 см. має висоту 18 м. Скільки жесті потрібно для її виготовлення, якщо на з‘єднання іде 10% матеріалу.

 

Задача 3

Лінолеум змотаний у рулон діаметром 70см.     Ширина рулону 3м, товщина лінолеуму 1см. Яка довжина лінолеуму, якщо діаметр труби, на яку його намотано – 8см?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Група  3  «Тіла обертання в автомобілях»

 

1 студенрт

Тіла обертання широко застосовуються в техніці, особливо в машинобудуванні. В цьому можна переконатися, якщо подивитися на форму різних приладів, агрегатів. Найпростіша деталь автомобіля —підшипник —.має в своєму складі тіло обертання—- кулю. Але чому саме кулю, а не куб або призму? 
         Та тому, що куля зазнає найменшого тертя під час роботи підшипників. У них вставляються кульки однакового розміру. Не можна вставити хоча б одну кульку більшу або меншу за розміром, бо це спричиняє люфт агрегатів автомобіля і призводить до ушкоджень. Важливим є також те, що складові частини кермової трапеції з'єднані не простими болтами, а кульовими з'єднаннями, бо під час повороту змінюються кути з'єднання і циліндричні болти можуть зламатися. 
Ще кулі використовують: 
      а) при перемиканні передач — кульки не дають змоги увімкнути відразу дві передачі; 
      б) у клапанних пристроях — у гідровакуумних насосах кулька перекочується в циліндрі під тиском або в результаті розряду то відкриває, то закриває шлях гальмовій рідині; 
      в) у гідропідсилювачі — при повороті керма перекочується в бік повороту і допомагає водієві повертати кермо. 

 

 

 

І1 студенрт
      Важливу роль в автомобілі відіграють циліндри. Циліндричні підшипники в автомобілях використовують там, де потрібні підшипники з великою бічною поверхнею і невеликою товщиною (наприклад, у механізмі зчеплення). 
      У формі циліндра зроблено найважливіші складові частини автомобіля: генератор, індукційну котушку, конденсатори, фільтри, насоси, стартер, карданну передачу, гідропідсилювач тощо. Тут використовується така властивість обертання навколо своєї осі: відстань від усіх зовнішніх точок до осі обертання однакова, що якраз ми спостерігаємо у циліндрі. 
        Головні робочі частини двигуна — поршні — теж мають форму циліндрів і знаходяться в своєрідних циліндрах. Під час переміщення поршня від верхньої мертвої точки до нижньої мертвої точки над ним утворюється простір, який називається робочим об'ємом циліндра. Коли поршень знаходиться у верхній мертвій точці, над ним утворюється найменший простір, який називається об'ємом камери згоряння. 
У багатоциліндрових двигунах повний об'єм усіх циліндрів виражається в літрах і називається літражем. Таким чином, визначення об'ємів циліндрів є головною характеристикою автомобіля. 
 

ІІ1 студенрт

         Чи використовуються в автомобілі конуси? У формі конусів виконано р. регулюючих гвинтів у різних частин; автомобіля (наприклад, на колесах). Використовуються також конічні підшипники. Голчасті клапани, виготовлені у формі конуса, використовуються у карбюраторі для регулювання подачі пального. У формі конуса виготовлені деякі деталі двигуна(головки клапанів, кульові пальці, поршень у головному гальмовому циліндрі). 
        Усе це свідчить про те, що такі тіла обертання, як куля, циліндр, конус, широко застосовуються як в машинобудуванні, так і в деяких інших галузях діяльності людини.

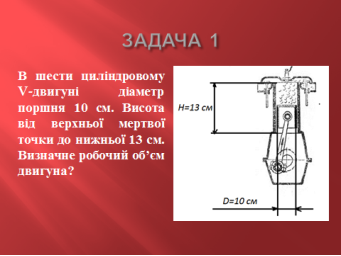
Задача 1

В шести циліндровому V-двигуні діаметр поршня 10 см. Висота від верхньої мертвої точки до нижньої 13 см. Визначне робочий об’єм двигуна?

Задача 2

Маса кульки дворядного сферичного підшипника дорівнює 3 грами. Який діаметр кулі? Густина матеріалу з якого виготовлена куля ρ=7,8 г/см³

 

Задача 3

         На напівпричіп К1040-3 встановлені дві циліндро-конічні  цистерни, призначені для перевезення борошна. Внутрішній діаметр циліндричної частини дорівнює 2400мм, діаметр завантажувального люка - 400 мм. Скільки борошна  (густина 0,46г/см ) може перевезти цей автомобіль, якщо висота циліндричної частини - 600 мм, а конічних - по 400 мм?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Група 4   «Тіла обертання і спорт»

1студент

     Геометрія – одна з найдавніших та найцікавіших наук. Вона вивчає геометричні фігури та їх властивості на площині та в просторі.

Знання з геометрії використовуються в багатьох сферах життя. Людина використовує геометричні фігури та їх властивості навіть не помічаючи цього. Ми можемо навести  багато прикладів  тіл обертання, але зупинимося на спорті, адже кожен з нас вважає спорт невід′ємною частиною життя.

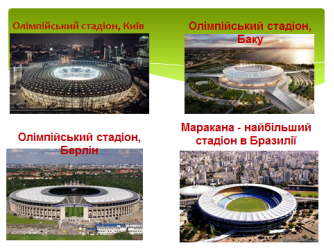
Циліндри, конуси, кулі - повсюди у спорті. Такі форми мають і  спортивні  споруди, і  спортивний інвентар,і , навіть , спортивні нагороди.

      Олімпійські стадіони  Києва, Берліна,Баку мають форму величезних циліндрів в середині яких розміщенні футбольні поля. Маракана – один з найбільших стадіонів світу знаходиться в      Ріо-де-Жанейро. Цей стадіон вважається головним храмом футболу в світі, тому що для Бразилії – футбол є другою релігією.

 

 

2 студент

       Важко назвати вид спорту у якому не використовується інвентар, що має форму тіл обертання. Циліндри  це:  хокейна шайба, різні  жердини,стійки воріт, камені кйорлінгу, бліни у важкій атлетиці.

     Конусами є – рапіри, стріли для дартсу, киї, тощо…

Куль та сфер у спорті дуже багато :  метальне ядро, гирі, різні м′ячі …

 

Пропонуємо роз′язати такі задачі

Задача 1 

      За вимогами ФІФА футбольний мяч  має задовольняти таким умовам

• М'яч повинен мати сферичну форму;

• м'яч виготовляється зі шкіри;

• має довжину кола не більше 70 смі не менше 68 см;

• на момент початку матчу важить не більше 450г і не менше 410г;

• має внутрішній тиск, рівний 0,6 −1,1 атмосфери  на рівні моря.

Внутрішній прошарок між покришкою та камерою займає підкладка. Якість футбольного м'яча взаємозалежна від товщини підкладки. Підкладка допомагає зберегти форму м'яча та відскок, виготовляється з поліестеру або пресованої бавовни.

Скільки матеріалу потрібно для виготовлення підкладки футбольного м'яча?

Задача 2

    Хоке́йна ша́йба — круглий гумовий дискіз діаметром 3 дюйми й товщиною 1 дюйм.

При вазі 170 г хокейна шайба розвиває швидкість до 160 км/год.

З якого матеріалу виготовлена  шайба? Якщо 1 дюйм становить: 2,54см.

 

Задача 3

У басейн  креслення якого ви  бачите на малюнку  налили 10 000 куб. м води.

Чи можна плавати у ньому?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Підбиття підсумків.

  Отже, ми бачимо. Що застосування математики в усіх галузях науки, господарства і життя – необмежене. Математика скрізь, вона – на кожному кроці.

  Наше суспільство потребує як талановитих дослідників, так і спеціалістів, які добре знають математику та здатні застосовувати свої знання на практиці.

Знання про тіла обертання, обчислення їх об'ємів та площ поверхонь використовуються в багатьох сферах людського життя.

 Оцінювання.

Наше змагання добігло кінця. Прошу вашу увагу на підсумкову таблицю. (всі студенти  оцінюються за даними таблиці).

Рефлексія .

Продовжити речення:

• На занятті я дізнався…
• На занятті я зрозумів…
• На занятті я навчився…
• Найлегшим було…
• Найцікавіше було…

 

Домашнє завдання.

1. Розв'язати по одній задачі від кожної грипи.
2. Підготуватися до тематичного оцінювання.

 

 

 

 

 

 

 

 

 

Підсумкова таблиця

Математичний диктант

Вірю не вірю

Задачі І групи

Задачі ІІ групи

Задачі ІІІ групи

Задачі ІV групи

Презентація

Доповідь

ВСЬОГО

ОЦІНКА