Урок "Розв'язування прямокутних трикутників"
УРОК – ГРА
Веселі перегони островом трикутників
(геометрія)
розрахований на 1 академічнy годинy
8 КЛАС
Вчитель математики Селятинського ЗЗСО І-ІІІ ст. ім. О. Зайця Політанська О.І.
Тема: Узагальнення та систематизація компетентностей
Мета:
Навчальна: закріпити та систематизувати знання учнів з теми «Розв’язування прямокутних трикутників».
Розвивальна: розвивати логічне мислення, прищеплювати вміння працювати в групах та стимулювати розвиток інтересу до вивчення математики.
Виховна: Виховувати позитивне ставлення учнів до навчально-пізнавальної діяльності.
Обладнання: гральний кубик, карта із завданнями, стікери, маркер, підручник, донка, анаграми, катрки з смайликами для вправи «Рефлексія».
Епіграф: «Предмет математика є на стільки серйозним, що корисно не втрачати випадку зробити його цікавим» Блез Паскаль
Девіз уроку: «Математика навчає мислити і разом із ним всиляє віру в безмежні сили людського розуму» В. Сухомлинський
Хід уроку
І. Організаційний етап
Вступне слово (привітання, налаштування на активну роботу)
ІІ. Формування мети і завдань уроку
Загальна мета уроку закріпити знання учнів з теми «Розв’язування прямокутних трикутників» та опанувати способи застосування цих знань; формувати вміння оперувати набутими знаннями в стандартних та нестандартних ситуаціях.
ІІІ. Повторення та систематизація набутих компетентностей
Правила гри
- Об’єднати учнів у три групи;
- За допомогою розгадування анаграм визначити ходів команд (Геометрія, трикутник, тригонометрія);
- По черзі учасники команд кидають гральний кубик, рухаються на ту кількість кроків які випали на гральному кубику та виконує завдання, яке розміщене на даному кроці;
- За кожне правильно розв’язане завдання команда отримує 3 бали.
- Команда, яка швидше дійшла до фінішу отримує 12 балів, інші команди розподіляють набрані бали між собою самостійно;
- Учасники команди можуть набрати додаткові бали допомагаючи розв’язувати завдання учасникам інших команд.
Завдання та короткі розв’язки до задач
- Що називають синусом гострого кута прямокутного трикутника?
Синусом гострого кута прямокутного трикутника називають відношення протилежного катета до гіпотенузи.
- Що називають косинусом гострого кута прямокутного трикутника?
Косинусом гострого кута прямокутного трикутника називають відношення прилеглого катета до гіпотенузи.
- Що називають тангенсом гострого кута прямокутного трикутника?
Тангенсом гострого кута прямокутного трикутника називають відношення протилежного катета до прилеглого.
- Сформулюйте теорему Піфагора?
У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.
- Уведіть поняття похилої та її перпендикуляра?
Нехай точка ![]() не лежить на прямій
не лежить на прямій ![]() ,
, ![]() – перпендикуляр цієї прямої. Будь-який відрізок, який сполучає точку
– перпендикуляр цієї прямої. Будь-який відрізок, який сполучає точку ![]() з прямою
з прямою ![]() і не збігається з перпендикуляром, називають похилою до прямої
і не збігається з перпендикуляром, називають похилою до прямої ![]() .
. ![]() – похила до прямої
– похила до прямої ![]() , точка
, точка ![]() – основа похилої, точка
– основа похилої, точка ![]() – основа перпендикуляра. Відрізок, який получає основу похилої й основу перпендикуляра, називається проекцією похилої.
– основа перпендикуляра. Відрізок, який получає основу похилої й основу перпендикуляра, називається проекцією похилої.
- Який трикутник називається єгипецьким?
Трикутник зі сторонами 3см, 4см, 5см – прямокутний, оскільки 32+42=52. Такий трикутник називається єгипецьким.
-
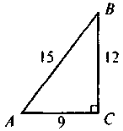 Знайти: cos В, tg А ◄
Знайти: cos В, tg А ◄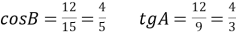 ►
►
-
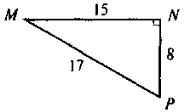 Знайти: sin Р, cos М ◄
Знайти: sin Р, cos М ◄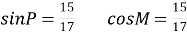 ►
►
-
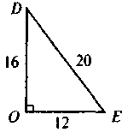 Знайти: tg D, sin E, ◄
Знайти: tg D, sin E, ◄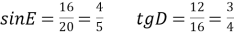 ►
►
-
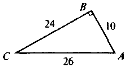 Знайти: sin A, cos A◄
Знайти: sin A, cos A◄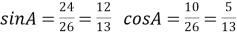 ►
►
-
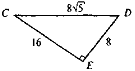 Знайти: tg D, tg C ◄
Знайти: tg D, tg C ◄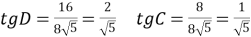 ►
►
-
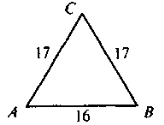 Знайти: cos A , cos В◄
Знайти: cos A , cos В◄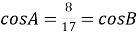 ►
►
-
Знайдіть гіпотенузу прямокутного трикутника, якщо катети дорівнюють
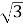 см і 1 см. ◄3+1=5
см і 1 см. ◄3+1=5 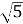 ►
►
- У колі радіусом 17 см проведено хорду. Знайдіть довжину хорди, якщо вона віддалена від центра на відстань 8 см. ◄289-64=225 Відповідь: 15см►
-
Знайдіть значення виразу
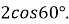 ◄
◄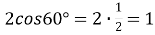 ►
►
-
Знайдіть катет прямокутного трикутника, якщо гіпотенуза і другий катет відповідно дорівнюють 2 см і
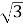 см. ◄4-3=1►
см. ◄4-3=1►
-
Визначте, який із кутів
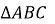 прямий, якщо
прямий, якщо 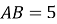 см,
см, 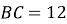 см,
см, 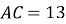 см. ◄
см. ◄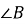 ►
►
-
Знайдіть сторони квадрата, діагональ якого дорівнює
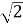 см.
см.
◄![]()
![]()
![]() ►
►
-
Знайдіть сторону рівностороннього трикутника, висота якого дорівнює
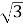 см.
см.
◄за теоремою Піфагора ![]()
![]()
![]()
![]()
![]() ►
►
- Знайдіть другу діагональ ромба, сторона якого дорівнює 17 см, а одна із діагоналей становить 30 см.
◄Точка перетину діагоналей ділить їх навпіл: 30:2=15
![]() , 8*2=16 ►
, 8*2=16 ►
- Знайдіть периметр прямокутного трикутника, якщо відношення його катетів та гіпотенуза відповідно дорівнюють 5:12 та 26см.
◄Нехай І катет – 5![]() , а ІІ катет -12
, а ІІ катет -12![]() . За теоремою Піфагора та заданим відношенням складемо рівняння
. За теоремою Піфагора та заданим відношенням складемо рівняння
![]()
![]()
![]()
![]()
![]() cm►
cm►
-
У рівнобедреній трапеції
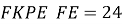 см,
см, 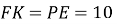 см,
см, 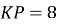 cм. Знайдіть синус кута
cм. Знайдіть синус кута 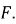
 ◄ Знайдемо довжину відрізків, які відтинають висоти
◄ Знайдемо довжину відрізків, які відтинають висоти ![]() см. За оберненою теоремою Піфгора знайдемо висоту
см. За оберненою теоремою Піфгора знайдемо висоту ![]() см.
см. ![]() ►
►
-
З точки
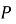 до прямої проведено дві похилі
до прямої проведено дві похилі 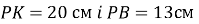 . Проекція похилої
. Проекція похилої 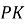 дорівнює 16 см. Знайдіть проекцію похилої
дорівнює 16 см. Знайдіть проекцію похилої 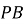 .
.
◄![]()
![]() ►
►
- Бісектриса гострого кута прямокутного трикутника ділить катет на відрізки 10 см і 26 см. Знайдіть гіпотенузу трикутника
 ◄ катет: 10+26=36 см, другий катет х
◄ катет: 10+26=36 см, другий катет х
За теоремою Піфагора гіпотенуза:
![]()
за властивістю бісектриси трикутника випливає
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Відповідь: 15см ►
IV. Підсумки уроку
- Вправа «Рефлексія».
Учні отримали картки із зображенням смайликів на яких є записи «Мені все зрозуміло. Все сподобалося», «Я майже все зрозумів. Я задоволений» та «Я майже нічого не зрозумів. Я не задоволений»
- Оцінювання учнів.
V. Домашнє завдання
Повторити § 18-21
Виконати «Завдання для перевірки знань § 18-21» ст. 150


про публікацію авторської розробки
Додати розробку
