Урок "Розв’язування вправ і задач на прогресії, в тому числі прикладного змісту". (9 клас)

Тема: Розв’язування вправ і задач на прогресії, в тому числі прикладного змісту. (9 клас)

Мета: повторити формули -го члена і суму арифметичної та геометричної прогресії, використовувати отримані теоретичні знання для розв’язання задач і вправ; розвивати інтерес до предмету, формування таких якостей особистості, як відповідальність, уважність і уміння аналізувати.

Тип уроку: урок застосування знань, умінь та навичок.  

Форма: індивідуальна та групова, фронтальна.

Обладнання і наочність: підручник, дошка, зошити, ноутбук, мультимедійна дошка.

Підручник: Мерзляк, Полонський, Якір, Алгебра 9 клас

Хід уроку

1. Організаційний момент. (1 хв.)
2. Повідомлення теми і мети урока. (5 хв.)

Доброго дня, діти! Сьогодні ми з вами по розв’яжемо деякі вправи і задачі на прогресію. Але спочатку розгадаємо кросворд.

3. Актуалізація опорних знань. (10 хв.)

Кросворд.

1. Арифметична прогресія, яка має від’ємну різницю, тобто d < 0 називається … .  (спадна)
2. Числова послідовність, у якої різниця між кожним членом, починаючи з другого, і попереднім є сталою величиною називається … прогресією. (арифметичною)
3. Функція, визначена на множині натуральних чисел називається … послідовністю. (числовою)
4. Рух вперед, поступове вдосконалення. (прогрес)
5. Числова послідовність відмінних від нуля чисел, у якій частка від ділення будь-якого члена, починаючи з другого, на попередній є сталою величиною називається … прогресією. (геометричною)
6. Один із способів задання послідовностей. (рекурентним)
7. Формула … перших 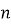членів геометричної прогресії: (суми)
8. Число 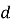називається … . (різницею)
9. Думка про щось бажане. (мрія)

Діти, давайте разом заповнимо схему. Вчитель обирає кого хоче з учнів по черзі, а учні в свою чергу повинні заповнити схему.

4. Засвоєння нових знань, умінь. (20 хв.)

Сумування.

Разом з кожною послідовністю можна розглядати й таку послідовність

Знаходження формули -го члена послідовності називають сумуванням перших n членів послідовності .

Оскільки ви знаєте формули обчислення суми n перших членів арифметичної і геометричної прогресій, то тим самим умієте сумувати перші n членів цих послідовностей.

За допомогою грецької літери (сигма) суму записують так: .

Наприклад,

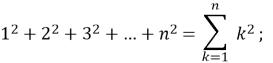
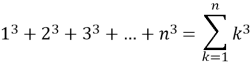
Одним з ефективних способів сумування є використання раніше доведених формул.

Завдання. Знайдіть суму

Прогресія – явище без перебільшення, унікальне. Історія виникнення прогресії сягає глибини віків.

Підсумовуванням арифметичних і геометричних прогресій та складанням відповідних задач займалися багато любителів математики протягом багатьох століть. В розвиток теорії про прогресіях внесли вчені Архімед, Піфагор та його учні, французькі математики Леонард Фібоначчі і Баше де Мезіріак, німецькі математики М. Штіфель, Н. Шюке, і К. Гаусс.

Найдавнішою задачею на прогресії є задача про розподіл хліба, записана в Єгипетському папірусі Ринда, яка відноситься до III ст. до н. е.

Перші задачі на прогресії пов’язані із запитами господарського життя і суспільної практики (розподіл спадщини, одержання винагороди), із спостережень над явищами природи, з досліджень суспільно-економічних явищ. Так, у вавилонських текстах розповідається про те, що збільшення освітленої частини місячного диска протягом перших п’яти днів відбувається за законом геометричної прогресії зі знаменником 2, у наступні 10 днів – за законом арифметичної прогресії з різницею 16. Широкий інтерес вавілонян до астрономії робить зрозумілим виникнення цієї задачі.

Тривале життя прогресій зумовлене не тільки їх цікавими математичними властивостями, а й широким застосуванням в інших науках. На сьогоднішньому уроці ми і будемо розв’язувати задачі на прогресії, , які ілюструють використання прогресій за межами математики . А ще послухаємо ваші повідомлення, які ви готували вдома, про застосування прогресій у різних сферах людської діяльності.

Задача 1. (Легенда про винахід шахів)

Шахову гру винайшли в Індії. Ознайомившись з нею, індійський принц Ширам, захоплений дотепністю і різноманітністю можливих ситуацій,  покликав до себе її винахідника, ученого Сету, і сказав йому: «Я хочу гідно нагородити тебе, Сета, за прекрасну гру, яку ти придумав. Я досить  багатий, і можу виконати будь – яке твоє бажання».

«Володарю, - відповів Сета, - накажи видати мені за першу клітинку шахівниці  одну пшеничну зернину, за другу – дві, за третю – чотири і далі за кожну клітинку вдвічі більше, ніж за попередню».

Принц здивувався, що винахідник так мало запросив. Але обіцянку не зміг виконати. Після ретельних підрахунків вияснилося, що кількість зерен, що бажає одержати Сета, така велика, що її не знайдеться на всьому просторі Землі. Для того, щоб видати нагороду, треба перетворити всі царства в поля,  висушити всі річки, озера, розтопити кригу і сніги. Увесь цей простір засіяти пшеницею й усе, що виросте на ньому за 5 років, віддати Сеті. Зі здивуванням слухав принц слова вчених. “Напишіть же мені це дивовижне число,”- сказав він.

Розв’язання. Маємо геометричну прогресію , в якій

В шахівниці 64 клітинки. Тому cпробуйте обчислити цю суму. Ми оцінимо тільки 264:

 І це наближене значення. Такої кількості зерна не зможуть зібрати всі країни світу  впродовж сотень років, яка  приблизно у 2000 разів більша від площі усієї поверхні Землі.

Задача 2. (Забавна арифметика, 1910 р.)

Одного разу розумний бідняк попросив у скупого багатія притулку на 2 тижні на таких умовах: «За це я тобі першого дня заплачу 1 крб., другого – 2 крб., третього 3 крб., збільшуючи щоденну плату на 1 крб. Ти ж будеш давати мені  милостиню: першого дня – 1 коп., другого дня – 2 коп., третього – 4 коп., і т.д. збільшуючи щодня милостиню вдвічі». Багатій з радістю погодився, вважаючи, що умови вигідні для нього. Скільки грошей отримав багатій?

Розв'язання: Сума, яку має сплатити бідняк за 14 днів, складає арифметичну прогресію,  в якій а , тобто 105 крб., а багатій сплачує суму, яка складає суму геометричної прогресії, в якій . Тому коп.  або 163 крб.83 коп. Отже, багатій, отримавши від бідняка 105 крб., заплатив йому 163 крб.83 коп., тобто,  за те, що бідняк у нього проживав 2 неділі, багатій заплатив йому 58 крб.83 коп. (вернувши при цьому і ті гроші, які одержав від бідняка).

Задача 3. Поливання грядок

У городі 30 грядок, кожна довжиною 16м і шириною 2,5м. Поливаючи грядки,  городник приносить відра з водою з колодязя, розташованого в 14м від краю городу, і обходить грядки вздовж межі, причому води, принесеної за один раз,  вистачає для поливання лише однієї грядки. Якої довжини шлях проходить  городник, поливаючи весь город? (Шлях починається і закінчується біля колодязя.)

Розв'язання: Для поливання першої грядки городник проходить шлях 14 + 2,5 + 16 + 2,5 + 16 + 14 = 65 (м).

Для поливання другої грядки він проходить шлях 14 + 2,5 + 16 + 2,5 + 16 + 2,5 + 2,5 + 14 = 70 (м).

Для кожної наступної грядки потрібно пройти шлях, на 5м довший за попередній. Маємо арифметичну прогресію: 65, 70, 75, …     d=5

Відповідь: Городник, поливаючи город, проходить шлях 4,125 км.

5. Застосування знань на практиці. (40 хв.)

Завдання 1. Мерзляк, Полонський, Якір, Алгебра 9 клас стр. 192 №1 і №3

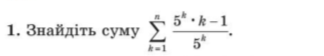
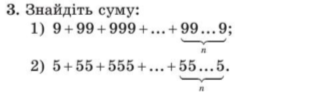
Завдання 2. Мерзляк, Полонський, Якір, Алгебра 9 клас №16.45, №17.41, №17.43, №18.51, №18.53, №19.13, №19.15

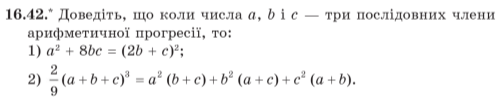
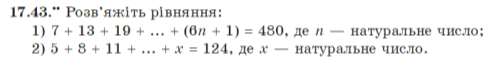
6. Підсумки урока. (2 хв.)

На уроці повторили арифметичну і геометричну прогресії та вирішили типові задачі.

7. Домашнє завдання. (2 хв.)

1. §3, п.16-20 повторити.
2. Виконати письмово: №19.12, №17.17, №18.39, стр. 192 №2, №4, №5.