Урок "Розв'язування вправ на означення логарифму"
Конспект уроку містить типові вправи на означення логарифму з детальними розв'язками вправ. Та розв'язаним домашнім завданням. Урок складено за підручником Шкіль М.І. Алгебра і початки аналізу: Підруч. Для 10 кл. загальноосвіт. Навч. закладів.
1
ПРАКТИЧНЕ ЗАНЯТТЯ №18
Показникова та логарифмічна функції.
Тема: Розв’язування вправ на означення логарифму.
Мета: навчальна: закріплення знань про логарифмічну функцію; набуття та вдосконалення навичок розв’язувати вправи за допомогою означення логарифму;
розвивальна: розвиток учбової активності, усної та самостійної роботи; розвиток логічного мислення, пам’яті, уваги;
виховна: виховувати відповідальність, самостійність.
Тип заняття: вдосконалення знань, вмінь, навичок.
Обладнання: роздатковий матеріал, підручники.
Завдання заняття:
- Усвідомлення сутності логарифму та меж його використання;
- Оволодіння навичками розв’язування вправ за допомогою означення логарифму;
- Усвідомлення навчального матеріалу теми всіма студентами за рахунок диференційованих завдань.
План заняття
|
Етапи заняття |
Методи та прийоми |
|
Бесіда |
|
Фронтальне опитування, індивідуальні завдання, робота біля дошки |
|
Розповідь |
|
Робота з підручником, самостійна робота студентів за картками |
|
Бесіда, пояснення |
Література:
- Алгебра і початки аналізу: Підруч. Для 10 кл. загальноосвіт. Навч. закладів / М.І. Шкіль, З.І. Слєпкань, О.С. Дубинчук.-К.: Зодіак-ЕКО, 2002.-272 с.
- А.М.Сайко Логарифмічна функція. Тести на встановлення відповідності: Математика в школах України №7 (271), 2010.
- І.Г.Тер-Нерсесова Логарифмічна функція, її властивості та графік: Математика в школах України №9 (273), 2010.
ХІД ЗАНЯТТЯ
І. Організаційна частина.
1. Привітання.
2. Перевірка готовності студентів до заняття.
3. Відмічення відсутніх.
ІІ. Актуалізація опорних знань.
Фронтальне опитування:
- Яка функція називається показниковою?
- Що називають експонентою?
- Яка область визначення показникової функції? Яка множина значень?
- Від чого залежить зростання / спадання функції?
-
Які з показникових функцій зростають, а які спадають
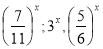 ,
, 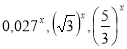 ? Чому? (Функції заздалегідь написані на дошці)
? Чому? (Функції заздалегідь написані на дошці)
- Дайте означення логарифму. (Декілька студентів)
- В чому суть основної логарифмічної тотожності?
- Дайте означення логарифмічної функції.
- Яка область визначення логарифмічної функції? Яка множина значень?
- Від чого залежить зростання / спадання функції?
- Які функції називаються оберненими?
- Запишіть основну логарифмічну тотожність.
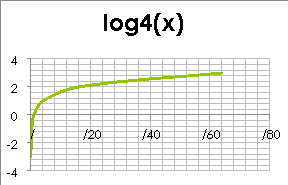
Робота біля дошки:
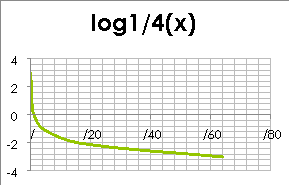
Два студенти на дошці будують графіки таких функцій: ![]() та
та ![]() . Інші два студенти, за допомогою графіка пояснюють властивості графіків.
. Інші два студенти, за допомогою графіка пояснюють властивості графіків.
ІІІ. Повідомлення теми, мети та завдань заняття та мотивація навчальної діяльності.
Тема нашого сьогоднішнього заняття: «Розв’язування вправ на означення логарифму». Сьогодні користуючись одним лише означенням логарифму та основною логарифмічною тотожністю, ми будемо розв’язувати різні завдання. Будемо працювати біля дошки, а також за індивідуальними картками.
Мотивація навчальної діяльності: Триста років тому в епоху Відродження почався бурхливий розвиток науки, техніки і мореплавства. Розвиток астрономії, а точніше астрономічних спостережень, вимагали нових методів обчислень, які були б доступні широкому колу людей. В основу таких методів і були покладені логарифми. Використання логарифмів дозволили дії другого ступеня (множення, ділення) звести до дій першого ступеня (додавання, віднімання) над відповідними логарифмами. При цьому довелося виконувати дії із значно меншими числами.
![]() Вміння обчислювати логарифми необхідні при розрахунках фізичних явищ, в астрономії (де вперше і виникла потреба використання логарифмів), в хімії і навіть в таких сферах мистецтва як музика та багато де інде.
Вміння обчислювати логарифми необхідні при розрахунках фізичних явищ, в астрономії (де вперше і виникла потреба використання логарифмів), в хімії і навіть в таких сферах мистецтва як музика та багато де інде.
Винахід логарифму пов’язаний з двома постатями: швейцарцем Іобстом Бюргі(1552-1632), знаним годинникарем і майстром астрономічних інструментів, і шотландцем Джоном Непером (1550-1617), який теж не був математиком за професією, астрономія була його «хобі». А Бюргі працював разом з астрономом Іоганном Кеплером. Саме величезний обсяг необхідних в астрономії обчислень і спонукав Бюргі і Непера шукати шляхів для їх спрощення. 20 років присвятив Непер своїм логарифмічним таблицям, аби, за його словами, «позбутися нудних і тяжких обчислень, відлякують зазвичай багатьох від вивчення математики». Обидва автори прийшли до своїх таблиць незалежно один від одного. Вони склали таблиці так званих натуральних логарифмів. Бюргі працював над таблицями 8 років і видав їх у 1620 році під назвою «Арифметична і геометрична таблиця прогресії». Проте його таблиці не отримали широкого поширення, бо Непер видав свій «Опис дивовижної таблиці логарифмів» на 6 років раніше. Тому і визнали число e неперовим числом.
ІV. Вироблення умінь та навичок застосовувати набуті знання на практиці.
Робота з підручником: [1, ст. 223]
І рівень
№ 176. Перевірити правильність рівності:
-
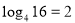 , за означенням логарифму
, за означенням логарифму 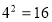 ,
,  . Пояснює викладач
. Пояснює викладач
-
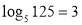 , за означенням логарифму
, за означенням логарифму 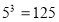 ,
, 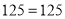 .
.
-
 , за означенням логарифму
, за означенням логарифму 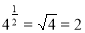 .
.
-
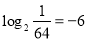 , за означенням логарифму
, за означенням логарифму  .
.
-
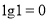 , за означенням десяткового логарифму
, за означенням десяткового логарифму 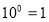 .
.
-
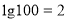 , за означенням десяткового логарифму
, за означенням десяткового логарифму 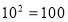 .
.
№ 177 Використовуючи знак логарифма, записати показник степеня з рівностей:
-
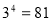 , за означенням логарифму
, за означенням логарифму 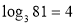 Пояснює викладач
Пояснює викладач
-
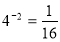 , за означенням логарифму
, за означенням логарифму 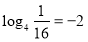
-
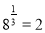 , за означенням логарифму
, за означенням логарифму 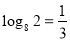
-
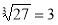 , спочатку з допомогою радикалів зробимо перетворення:
, спочатку з допомогою радикалів зробимо перетворення: 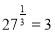 за означенням логарифму
за означенням логарифму 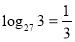
ІІ рівень
№ 182 Записати у логарифмічному вигляді:
-
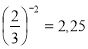 , за означенням логарифму:
, за означенням логарифму: 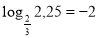
-
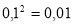 , за означенням логарифму:
, за означенням логарифму: 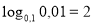
-
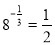 , за означенням логарифму:
, за означенням логарифму: 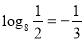
-
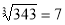 ; спочатку перетворимо рівність
; спочатку перетворимо рівність 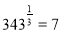 , за означенням логарифму:
, за означенням логарифму: 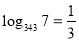 .
.
№ 180 Знайти число ![]()
-
 , для знаходження
, для знаходження 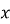
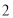 ) потрібно піднести основу (5), щоб отримати
) потрібно піднести основу (5), щоб отримати 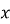
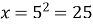 ; Пояснює викладач
; Пояснює викладач
-
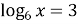 , для знаходження
, для знаходження 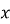
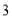 ) потрібно піднести основу (6), щоб отримати
) потрібно піднести основу (6), щоб отримати 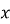
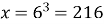 ;
;
-
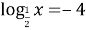 , для знаходження
, для знаходження 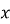
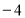 ) потрібно піднести основу (
) потрібно піднести основу (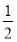 ), щоб отримати
), щоб отримати 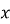
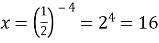 ;
;
-
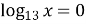 , для знаходження
, для знаходження 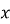
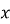
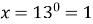 ;
;
-
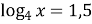 , для знаходження
, для знаходження 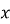
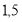 ) потрібно піднести основу (4), щоб отримати
) потрібно піднести основу (4), щоб отримати 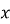
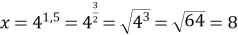 ;
;
-
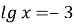 , для знаходження
, для знаходження 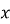
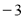 ) потрібно піднести основу (10), щоб отримати
) потрібно піднести основу (10), щоб отримати 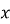
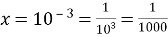 ;
;
№ 193 Знайти значення виразу:
ІІІ рівень
№ 194 Знайти значення виразу:
V. Підсумок заняття, повідомлення домашнього заняття.
На занятті ми розв’язували завдання, користуючись визначенням логарифму, а також основною логарифмічною тотожністю. На наступному вивчимо правила обчислення логарифмів.
Виставлення оцінок.
Домашнє завдання (роздатковий матеріал).
Домашнє завдання містить аналогічні завдання:
І рівень
Завдання №1. Записати у вигляді логарифмічних рівностей:
![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
Завдання №2. За означенням логарифму, перевірити справедливість таких рівностей:
![]() , ця рівність правильна оскільки
, ця рівність правильна оскільки ![]() .
.
![]() , ця рівність також справедлива, бо
, ця рівність також справедлива, бо ![]() .
.
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
Завдання №3. Користуючись основною логарифмічною тотожністю ![]() обчислити:
обчислити:
![]() ,
,
![]() ,
,
![]() .
.
ІІ рівень
Завдання №4 Знайти число ![]()
-
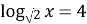 , для знаходження
, для знаходження 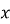
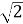 ), щоб отримати
), щоб отримати 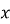
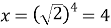
-
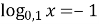 ,
, 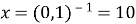
-
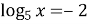 ,
, 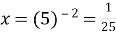
-
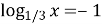 ,
, 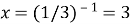
-
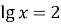 ,
, 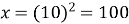
-
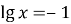 ,
, 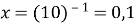
-
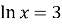 ,
, 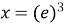
-
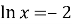 ,
, 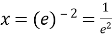
ІІІ рівень
№ 196, 219


про публікацію авторської розробки
Додати розробку