Тема.  Пряма Ейлера. Коло дев’яти точок

Мета: пригадати означення ортоцентра і центроїда; дати означення прямі Ейлера та познайомити з визначними точками; формувати навики розв’язування задач, навики роботи з додатковою літературою; розвивати логічне мислення, просторову уяву; виховувати охайність у ведені записів.

Тип уроку: засвоєння нових знань, умінь.

 

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання

З метою економії часу перевіряються лише відповіді та коротко обговорюється план розв’язування задач домашнього завдання по готовому рисунку.

ІІІ. Формулювання мети і завдань уроку

З кожним трикутником пов’язано багато особливих ліній і точок, а саме: висоти, медіани, бісектриси, ортоцентр, центроїд, прямі Чеви, пряма Менелая.

Розглянемо не менш цікаві точки і лінії в трикутнику, а саме: точки Ейлера, коло Ейлера, пряма Ейлера.

ІV. Актуалізація опорних знань та вмінь

З метою успішного засвоєння учнями змісту нового матеріалу уроку необхідно активізувати їх знання  про:

1. Як знайти центр описаного кола? ( точка перетину серединних перпендикулярів – О)

2. Як знайти центр вписаного кола, інцентр? ( точка перетину бісектрис – J)

3. Яку точку називають ортоцентром трикутника? ( точку перетину прямих які містять висоти трикутника  –  Н )

4. Як називають точку перетину медіан трикутника? ( центроїд –  М )

Точки О, J, Н, М називають чудовими точками трикутника. Використання такого емоційного епітета цілком обґрунтовано. Адже цим точкам притаманний цілий ряд красивих властивостей. Хіба не чудово вже те, що вони є в будь-якому трикутнику?

V. Сприйняття та усвідомлення нового матеріалу

Історична довідка

Леонард Ейлер (1707–1783) був не лише одним з найславетніших математиків в історії людства, а й на диво різнобічно обдарованим ученим. 

Жив Ейлер у м. Базель, Німеччина. Після закінчення університету в 1727 році він був запрошений в Росію працювати в Петербурзькій Академії, де читав лекції з фізики і математики. Ейлер створює фундаментальні праці з усіх галузей математики. У 1739 році опублікував тракт з музики, в якому виклав теоретичні основи будови музичних інструментів.

У 1741 році Леонард Ейлер повертається на батьківщину і працює в Берліні, на посаді директора математичного відділу берлінської Академії наук. Він пише багато ґрунтовних праць з астрономії, морської науки та інші.

У 1766 році, на прохання Катерини ІІ, Ейлер із сім’єю повертається в Росію.

Невдовзі після приїзду до Петербурга Леонард остаточно осліп       ( ще у 1735 році внаслідок надзвичайно напруженої праці Ейлер захворів на нервову гарячку і під час хвороби втратив праве око) і міг тільки диктувати свої твори, виконуючи основні обчислення усно. Та працездатність ученого, якому близько 60 років, не тільки не зменшилась, а ще більше зросла.

У 1769 – 1771 роках учений видав три томи під спільною назвою «Діоптрика», в якій виклав загальну теорію діоптрики –  науки, якої до нього взагалі не існувало.

У книзі «Листи до німецької принцеси» Ейлер популярно виклав багато питань з фізики, астрономії, хімії, математики і філософії. Твір видавався близько 40 разів дев’ятьма європейськими мовами.

До останніх днів Ейлер не залишав наукової роботи.

     У геометрії багато понять названо ім’ям Леонарда Ейлера.

План вивчення нового матеріалу

1. Теорема. Пряма Ейлера.

2. Лема.

3. Точки Ейлера.

4. Теорема Ейлера. Коло дев’яти точок або коло Ейлера.

Теорема. У будь-якому трикутнику центр описаного кола, центроїд і ортоцентр лежать на одній прямій.

Цю пряму називають прямою Ейлера.

Доведення.

Доведення для рівнобедреного трикутника є очевидним.

В прямокутному трикутнику ортоцентр – середина гіпотенузи, тоді всі три точки належать медіані, проведеній до гіпотенузи.

Доведемо теорему для гострокутного різностороннього трикутника.

   Оскільки точка М₁ – середина ВС, то АМ₁ –  медіана  ∆АВС. Нехай АМ₁ ∩ НО в точці М.

   Оскільки  АН || ОМ₁, то НАМ =            = ОМ₁М як внутрішні різносторонні. Крім  того, АМН = М₁МО як вертикальні. Отже,   ∆НАМ ~ ∆ОМ₁М  за  двома  кутами.  Звідси   АМ : ММ₁ =          = АН : ОМ₁ =  НМ : МО = 2. Отже, точка М ділить медіану АМ₁ у відношенні 2 : 1, рахуючи від вершини А і 2ОМ = МН. Звідси точка М – центроїд ∆АВС.

Доведення для випадку тупокутного трикутника аналогічне.

Лема. Три чудові точки трикутника, центр описаного кола, центроїд і ортоцентр, лежать на одній прямі, причому 2ОМ =     = МН.

Означення. Середини відрізків висот від ортоцентра до вершин трикутника називаються точками Ейлера ( Е ).

Теорема Ейлера. Основи медіан, основи висот і точки Ейлера лежать на одному колі, яке називається колом дев’яти точок або колом Ейлера.

Доведення.

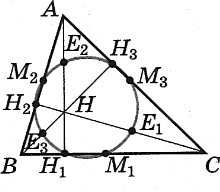
       Нехай М₁, М₂, М₃ – середини сторін ∆АВС; АН₁, ВН₂, СН₃ – його висоти; Н – ортоцентр, E₁, Е₂, Ез – точки Ейлера.

      Опишемо навколо ∆М₁M₂M₃ коло. Доведемо, що Н₁ (основа висоти АН₁) і точка Ейлера Е₂ (середина відрізка ВН) лежать на цьому колі. Дійсно, Н₁М₃ – медіана прямокутного  ∆АВН₁, проведена з вершини прямого кута, Н₁М₃ = ½АВ.

За властивістю середньої лінії М₁М₂ ∆АВС маємо:  М₁М₂  =  ½АВ. Отже, Н₁М₃ = М₁М₂.

Крім того, М₂ М₃ || М₁Н₁ (М₂М₃ || ВС за властивістю середньої лінії). Отже, трапеція М₁М₃М₂Н₁ – рівнобічна, а тому коло, яке проходить через три її вершини М₁, М₂, Мз, пройде і через четверту вершину Н₁.

Пряма М₃Е₂ || АН (М₃Е₂ – середня лінія ∆ВАН), пряма М₃М₂ || ВС (М₃М₂ – середня лінія ∆АВС), за умовою АН ВС. Отже, М₃Е₂ М₃М₂, тобто Е₂М₃М₂  = 90º.

Пряма M₁E₂ || АН  (М₁Е₂ – середня лінія ∆ВНС), пряма М₁М₂ || АВ (М₁М₂ – середня лінія ∆АВС), за умовою СН АВ. Отже, М₂Е₁ М₁М₂, тобто E₂M₁M₂ = 90º.

Навколо чотирикутника М₃Е₂М₁М₂ можна описати коло, тому що сума протилежних кутів дорівнює 180º.

Таким чином, коло, яке проходить через три точки М₁, М₂, М₃, проходить і через точки Ні і Е₂.

Аналогічно можна показати, що це коло пройде ще через точки Е₁, Е₃, Н₂, Н₃. Отже, основи медіан, основи висот і точки Ейлера лежать на одному колі.

VІ. Закріплення та осмислення нового матеріалу

№1. Відновіть трикутник АВС за трьома даними точками: вершиною А, ортоцентром Н і точкою перетину серединних перпендикулярів О.

№2. Довести, що радіус кола дев’яти точок дорівнює , де R – радіус кола, описаного навколо трикутника.

Доведення.

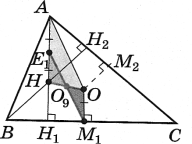
З’єднаємо точку М₁ з центром кола дев’яти точок О₉. Пряма М₁О₉ перетинає висоту АН₁ у точці Е₁. Е₁М₁ – діаметр кола дев’яти точок. ∆О₉М₁О = ∆О₉Е₁Н за другою ознакою ( НО₉ = = О₉О за доведеним, Е₁О₉ = О₉М₁ як радіуси кола Ейлера і Е₁О₉Н = ОО₉М₁ як вертикальні). Звідси ОМ₁ =  НЕ₁.  Оскільки ОМ₁ || НЕ₁    (як два перпендикуляри до ВС) і АЕ₁ = НЕ₁ , то чотирикутник АОМ₁Е₁ – паралелограм. Тоді М₁Е₁ = ОА, де М₁Е₁ – діаметр кола дев’яти точок, а ОА – радіус кола, описаного навколо трикутника. Отже, радіус кола дев’яти точок дорівнює .

№3. Довести, що відрізки М₁Е₁, М₂Е₂, М₃Е₃ мають спільну середину.

Доведення.

За доведенням чотирикутник ОМ₁НЕ₁ – паралелограм. Аналогічно можна довести, що  чотирикутники ОМ₂НЕ₂ і ОМ₃НЕ₃ – також паралелограми. Всі вони мають спільну діагональ ОН, середина якої є спільною серединою розглядуваних відрізків.

 

 

 

 

VІІ. Підсумки уроку

Вірите чи ні, що якщо кожний день по десять годин тільки переписувати труди Леонардо Ейлера, то не вистачить і сімдесяти шести років?

Так. Зібрання його творів склали 75 великих томи. Про нього говорили, що він «обчислює так, як людина дихає».

Контрольні запитання.

1. Які точки називають чудовими точками трикутника?

2. Які чудові точки лежать на одній прямі?

3. Сформулюйте лему.

4. Сформулюйте теорему Ейлера.

 ІХ. Домашнє завдання

Вивчити зміст засвоєних на уроці понять.

№1. Відновіть трикутник АВС за центром описаного кола, ортоцентром і серединою сторони ВС.

№2. Точки В, С, М, J, Н трикутника АВС належать одному колу. Знайдіть його кути.

             Розв’язання.

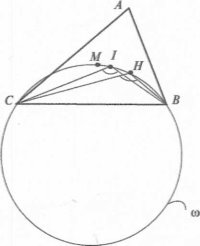
Очевидно, що ∆АВС – гострокутний (оскільки М та J знаходяться всередині ∆АВС, то й ортоцентр Н згідно з умовою повинен знаходитися всередині ∆АВС). ВНС = ВJС як вписані, що спираються на одну дугу в колі ω.

 

 

ВНС = 180º – А ,  ВJС = 90º + ½ А.  Тоді 180º – А = 90º + ½А, звідки А = 60º. Отже, ВНС = ВJС = 120º. Центральний ВОС = 2А = 120º. Таким чином, точки О, J і Н належать колу. З іншого боку, точки О, М, Н належать одній прямі – прямій Ейлера. Отже, точки співпадають. Значить ∆АВС – рівносторонній, а А = В = С = 60º.

Відповідь: 60º.

 

 

№3. (Наукова робота) Довести теорему про медіани трикутника.

Перша група за подібністю трикутників.

Друга група за теоремою Менелая.

    Третя група за прямою Ейлера.

 

№1. Перша група доводила теорему про медіани трикутника за подібністю трикутників.

Доведення.

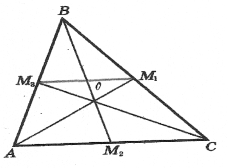
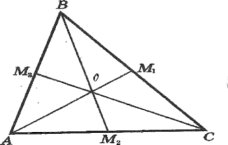
     В ∆AВС  АМ₁, ВМ₂, СМ₃ медіани, які перетинаються в точці О. Проведемо М₁М₃ – середню лінію ∆AВС. За властивістю середньої лінії М₁М₃ || АС М₁АС =АМ₁М₃, М₃СА = СМ₃М₁ як внутрішні різносторонні при паралельних прямих та січні. Тоді ∆AОС ~  ∆М₁ОМ₂  за двома кутами.  Звідси АО : ОМ₁ =   СО : ОМ₃ =      = АС : М₁М₃. За властивістю середньої АС = = 2М₁М₃, то АО : ОМ₁ = СО : ОМ₃ = 2 : 1. Аналогічно доводиться, що ВО : ОМ₂ =        = 2 : 1.

 

Друга група доводила за теоремою Менелая.

                               

 

                                                Доведення.

    В ∆AВС  АМ₁, ВМ₂, СМ₃ медіани , які перетинаються в точці О. Пряма М₃С перетинає  сторони АВ і ВМ₂ ∆АВМ₂ та продовження  сторони АМ₂. Тоді за теоремою Менелая · · =  1 або 1 · · = 1. Звідси = .

Третя група за прямою Ейлера.

Доведення.

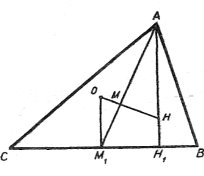    В ∆AВС  АМ₁ медіана, АН₁ висота, точка О – центр описаного кола і точка Н – ортоцентр. Позначимо через М точку перетину відрізків ОН і АМ₁. Оскільки       АН₁ ВС і ОМ₁ ВС (ОМ₁ – серединний перпендикуляр), то ∆ОМ₁М ~ ∆НАМ за двом кутами (ОММ₁ = АМН як вертикальні і ОМ₁М = МАН як внутрішні різносторонні). Отже, за лемою   АМ : М₁М = 2 : 1. Аналогічні міркування мають місце у випадку медіан ВМ₂ і СМ₃. Медіани будуть ділитися точкою М у відношенні  2 : 1, рахуючи від вершин.