Тема. Властивість дотичної до кола та січної

Мета: дослідити залежність між дотичною та січною; показати її застосування при розв’язуванні задач; виховувати наполегливість, вміння відстоювати свою думку; розвивати увагу, зорову пам'ять, математичну  мову, кмітливість, уміння само перевіряти  і аналізувати свої помилки.

Тип уроку: засвоєння нових знань, умінь.

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання

Оскільки вправи домашньої роботи відтворювали  ситуації, аналогічні  до

розглянутих на попередньому уроці, перевіряється лише наявність виконаного домашнього завдання і якщо виникли в учнів запитання під час його виконання, то дати відповідь.

Рівень засвоєння знань та вмінь попереднього уроку перевіримо під час виконання математичного диктанту.

                 Математичний диктант.

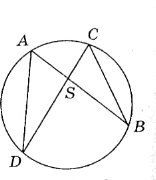
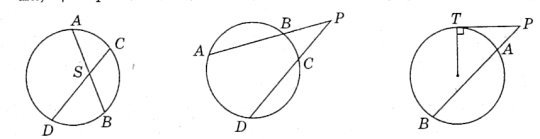
    На рисунку  хорди АВ і CD перетинаються в точці S. Закінчіть речення так, щоб утворило­ся правильне  твердження.

    1.Кут СSВ  дорівнює куту... .

    2.Кут DAB дорівнює куту... .

    3.Кут СВS дорівнює куту... .

    4.Трикутник ASD подібний до трикут­ника... . 

    5.Відношення АD : СВ дорівнює відношенню... .

    6. Якщо AS = 8 см, SB = 9 см, CS = 3 см, то SD дорівнює...

ІІІ. Актуалізація опорних знань та вмінь.

Виконання усних вправ

     Дати означення дотичної до кола та січної.                                                         

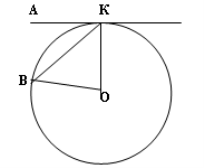          Дано:   хорда ВК стягує  дугу  в  54°,      

    проведена дотична АК до кола в точці К.                                                                                                                                                                                                                        

           Знайти:  кути, утворені хордою та

    дотичною.                                                   

                            Розв’язання.                                          

Кут  між  дотичною  і  хордою  дорівнює половині градусної міри дуги, яку стягує хорда.   Тому АКВ = ½ · 54° =  27º.

 ІV. Формування мети і завдань уроку, мотивація навчальної діяльності

Геометрія залізничних колій на поворотах є доволі складною. Будівниц­тво таких доріг вимагає розв'язання складних задач, деякі з них ми зможемо розв'язати в 8–9 класах.

При будівництві доріг, коли треба змінити напрям, не роблять крутих поворотів, а переходять від одного до другого напряму плавно,здебільшого по дузі кола.

Для безпеки руху дуги кола повинні мати доволі великі радіуси. Примі­ром, для залізничної колії вони мусять бути не меншими 600 м  а, як правило, дорівнюють 1 км і навіть 2 км.

Якщо стики прямих і кіл залишити не плавними при переході від пря­молінійної ділянки (дотичної) до криволінійної (дуги кола) або навпаки, то вагони потяга зазнаватимуть удару, від чого швидко зношуватимуться рейки й колеса, розхитуватимуться кріплення вагонів.

Можна сказати, що геометрія є співавтором проектів доріг, вона гаран­тує безпеку руху на них.                                      

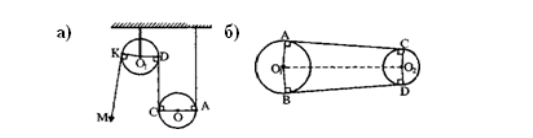На рисунку а) зображено два блоки, за допомогою яких під­німається вантаж. На рисунку б) зображено пасову передачу, яка з'єднує два шківи. У всіх цих випадках маємо справу з поняттям  «дотична».                                    

Сьогодні ми з вами на уроці проведемо наступне  дослідження. Об’єкт дослідження: хорда і дотична. Предмет дослідження: залежність між хордою та дотичною.

V. Сприйняття та усвідомлення нового матеріалу

З точки, що знаходиться поза  колом,  проведено дотичну АС  і  січну АВ. З точки дотику проведено дві хорди СВ і СЕ.       

       Завдання.

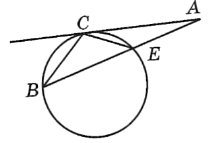1. Знайдіть подібні трикутники.
2. Доведіть їх подібність.
3. Складіть пропорцію.
4. Зробіть висновок.

   ∆АЕС ~ ∆АСВ за двома кутами (САВ – спільний, АСЕ =СВЕ= = ½СЕ). Звідси АС : АЕ = АВ : АС;  АС² = АЕ · АВ.

Який висновок ми можемо зробити? ( квадрат дотичної дорівнює добутку січної на її зовнішню частину).

VІ. Закріплення та осмислення нового матеріалу

№1.Через точку А проведено до кола дотичну АМ (М – точка дотику) і  січну,  яка  перетинає коло в точках  К і  Р  ( точка К лежить між точками А і Р). Знайдіть КР, якщо АМ = 12 см, АР = 18см.

№2. Із зовнішньої точки кола проведено дотичну завдовжки 6см і січну, довжина внутрішнього відрізка 5 см січної. Знайти довжину зовнішньої частини січної.

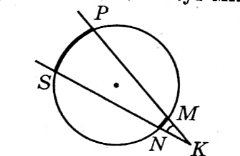
№3. Через точку К, яка лежить поза колом, проведено дві прямі, одна з яких перетинає коло в точках М і Р ( точка  М лежить між точками К і Р), а друга – у точках N і S ( точка N лежить між точками S і Р).

1. Доведіть, що КМ · КР =  КN · КS.

2. Знайдіть КS, якщо КМ = 18см, МР = 12см і КN : NS = 5 : 7.

Доведення.

      З’єднаємо точки Р і N та точки S і М. Розглянемо  ∆КРN і ∆КSМ. В трикутниках К спільний і Р = S так як спираються на одну дугу МN. Тоді ∆ КРN ~ ∆КSМ за двома кутами. Звідси КР : КS = КN : КМ . Отже, КМ · КР =  КN · КS.

Розв’язання.

Так як КМ = 18см і МР = 12см, то КР = 30см. Нехай х – коефіцієнт пропорційності, то КN = 5х і NS = 7х. Маємо: 18 · 30 = 5х · 7х; х² = 9; х = 3 або х = -3 – не задовольняє умову задачі. Отже, КS = (5 + 7) · 3 = = 36(см).

Відповідь: 36см.

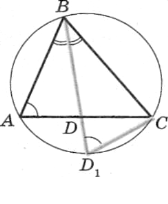
№4. У трикутнику  АВС  проведено бісектрису ВD. Доведіть, що ВD² = АВ · ВС – АD · DС.

                                                 Розв’язання.

            Продовжимо ВD до перетину з колом  в

     точці D₁. ВАС =ВD₁С  як  вписані, що

     спираються на  одну  й  ту  саму  дугу.АВD =

      = D₁ВС  за  властивістю  бісектриси.   

         Тоді   ∆АВD  ~  ∆D₁ВС  за  двома кутами.

     Звідси АВ : ВD₁ = ВD : ВС,   тобто  АВ · ВС  = 

 = ВD₁ · ВD.  Оскільки ВD₁  =  ВD + DD₁,  то  АВ · ВС  =  ВD²  +  ВD ×

 × DD₁. За  властивістю  хорд,  які перетинаються ВD · DD₁ = АD · DС. 

Тоді АВ · ВС = ВD² + АD · DС. Звідси ВD²  =  АВ · ВС –  АD · DС.

Ми з вами вивели формулу Лагранжа.

VІІ. Підсумки уроку

1. Сформулюйте властивість хорд, які перетинаються.
2. Сформулюйте властивість дотичної та січної, проведених до кола через одну точку.
3. Сформулюйте властивість січних, проведених до кола через одну точку.
4. Під кожним рисунком записати метричні співвідношення

у колі.

VІІІ. Домашнє завдання

Вивчити зміст засвоєних на уроці понять.

№1. Із точки поза колом проведено дотичну, довжина якої 12см. Обчисліть радіус кола, якщо відстань від цієї точки до кола 9см.

№2. У рівнобедреному трикутнику основа і бічна сторона відповідно дорівнюють 5см і 20см. Знайдіть бісектрису трикутника, проведену до бічної сторони.

                                                             Розв’язання.

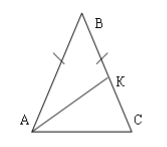На рисунку в ∆АВС АВ = ВС = 20см, АС = 5см.  Знайдемо бісектрису АК.  За  властивістю бісектриси АВ : АС = ВК : КС. Звідси   ВК : КС = 20 : 5; ВК : КС = 4 : 1. 

    Нехай  КС = х см,  тоді  ВК = 4х см. Маємо:    х + 4х = 20; х = 4(см). Отже, КС = 4см, а ВК =     = 16см.

    За формулою Лагранжа АК² = 20 · 5 – 16 · 4;                               

АК = 6см.

      Відповідь: 6см.