Тема.  Теорема Менелая, теорема Чеви

Мета: довести теорему Менелая і Чеви; показати їх застосування до розв’язуванні задач; формувати навики роботи з додатковою літературою; розвивати кругозір; сприяти виникненню в учнів інтересу до вивчення геометрії, усвідомлення її краси та значущості.

Тип уроку: засвоєння нових знань, умінь.

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання

Перевірка правильності виконання домашнього завдання шляхом пояснення розв’язання по заздалегідь підготовленим рисунком.

ІІІ. Формулювання мети і завдань уроку

Сьогодні ми продовжимо знайомиться з дивовижними теоремами.

Теорема Чеви – це класична теорема геометрії трикутників.

Теорема Менелая гарна і проста, але в шкільному курсі вона загубилась серед задач. Між тим вона входить в золотий фонд  давньогрецької математики.

ІV. Актуалізація опорних знань та вмінь.

Запитання.

1. Сформулюйте властивість дотичних проведених з однієї точки.

2. Сформулюйте теорему про бісектриси трикутника.

V. Сприйняття та усвідомлення нового матеріалу

Історична довідка

Менелай Олександрійський ( І - ІІ ст. н.е.) давньогрецький математик і астроном, жив і працював у Римі. Теорема названа в його честь доведена в третій книзі «Сферики» (1758р.). Менелай спочатку доводив її для плоского випадку, а потім для великих кіл на сфері. Ще ім’ям Менелая названий кратер на видимому боці Місяця.

Теорема Менелая використовується там, де потрібно довести, що три точки належать одній прямі.

Нагадаємо як називаються точки, які лежать на одній прямі?           ( колінеарними).

Теорема Менелая. Якщо пряма А₁В₁ перетинає сторони СВ і СА і продовження сторони АВ трикутника АВС відповідно у точках А₁, В₁, С₁, то      · · = 1.

Доведення.

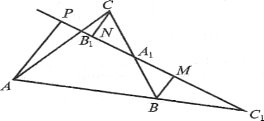  З вершин А,В,С ∆АВС опустимо перпендикуляри  АР, СN, ВМ на пряму А₁В₁. ∆АРС₁~ ∆ВМС₁ за двома кутами  ( Р = М = 90° і С – спільний). Звідси = . ∆А₁МВ ~ ∆А₁NС за двома кутами (СА₁N = ВА₁М як вертикальні і N = М = 90°). Звідси = . ∆АРВ₁ ~  ∆В₁NС за двома кутами ( РВ₁А =NВ₁С        як вертикальні і  Р = N = 90°). Звідси = . Тоді маємо:     · · =    ·  · = 1.

Зауважимо, що теорема справедлива й тоді, коли точки А₁ і В₁ лежать не на сторонах ∆АВС, а на їх продовженнях.

 Історична довідка

  Джованні Чеви (1648 – 1734) – італійський інженер-гідравлік і математик. Народився в Мілані, працював інженером у провінції Мантуї. Сучасники вважали його видатним спеціалістом у галузі економіки. Найважливішою заслугою є вчення про січні. Вчення викладені в праці «Про взаємно перетині прямі» (1678 р.). Вони започаткували нову синтетичну геометрію. У цій книзі сформульована і доведена теорема Чеви про властивість прямих.

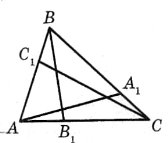На сторонах ВС, АС і АВ трикутника АВС візьмемо довільні точки А₁, В₁, С₁. Кожен з відрізків АА₁, ВВ₁, СС₁ називають чевіаною трикутника АВС.

Якщо чевіани є бісектрисами, або медіанами, або висотами гострокутного трикутника, то ці чевіани перетинаються в одній точці.

Теорема Чеви. Для того щоб чевіани перетиналися в одній точці необхідно, щоб виконувалася рівність · · = 1.

                                                  Доведення.

До трикутників АВВ₁ і СВВ₁ та прямих СС₁ і АА₁ відповідно застосуємо теорему Менелая. ·   · = 1; 

  · · = 1.

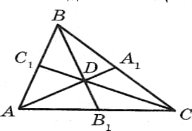  Звідси  · · = · · .

  Звідси  · = ·    або

· · = 1.

VІ. Закріплення та осмислення нового матеріалу

№1. Точка С₁ ділить сторону АВ трикутника АВС у відношенні     2 : 1. Точка В₁ лежить на продовженні сторони АС за точку С і АС = = СВ_1. Знайти у якому відношенні пряма В₁С₁ ділить сторону ВС.

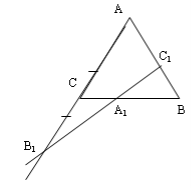                            Розв’язання.

     В ∆АВС точка С₁ є АВ і = 2, точка В₁ є  прямі АВ і АС = СВ₁ , тоді = . Знайдемо                                                                                               

      За теоремою Менелая · · = 1.

Отже, 2 · · = 1; = 1.

    Відповідь: = 1.

№2. На стороні ВС трикутника АВС обрано точку N так, що       ВN : NС =   2 : 3. У якому відношенні медіана ВМ ділить відрізок АN?                                                                  

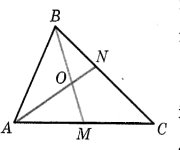                                             Розв’язання.

                                   На рисунку у  ∆АВС ВМ ∩ АN в точці О. За                                                   

                             умовою = . Знайдемо .

                                   Пряма ВМ  перетинає дві сторони  ∆АNС. Тоді

                             за   теоремою Менелая · · = 1.

За умовою = , а  за  властивістю медіани  = 1, отримуємо: 1 · · = 1. Звідси  = .

Відповідь: 5 : 2.

№3. Нехай А₁, В_1,С₁  – точки дотику вписаного кола в ∆АВС до сторін ВС, АС, АВ відповідно. Доведіть, що АА₁, ВВ₁, СС₁ перетинаються в одній точці.

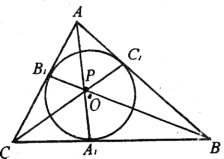Доведення.

    За властивістю дотичних , проведених з однієї     точки до кола, маємо:  ВС₁ = ВА₁,  СА₁ = СВ₁, АВ₁ = АС₁. Тоді · · = = · · = 1. За теоремою Чеви прямі АА₁, ВВ₁, СС₁ перетинаються в одній точці.

№4. Довести, що бісектриси трикутника перетинаються в одній точці.

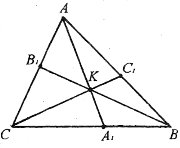Доведення.

   За властивістю бісектрис ∆АВС маємо: = ; = ; = . Перемножимо ці  рівності  і  одержимо:    · · =

· · = 1. Отже, за теоремою Чеви, бісектриси АА₁, ВВ₁, СС₁ ∆АВС перетинаються в одній точці.

VІІ. Підсумки уроку

Контрольні запитання.

1. Сформулюйте теорему Менелая.

2. Коли вона використовується?

3. Сформулюйте теорему Чеви.

4. Коли вона використовується?

 ІХ. Домашнє завдання

Вивчити зміст засвоєних на уроці понять.

№1. На сторонах АВ, ВС і СА трикутника АВС позначено точки С₁, А₁, В₁ відповідно так, що прямі АА₁, ВВ₁, СС₁ перетинаються в точці О. Пряма, яка проходить через точку О паралельно стороні АС, перетинає відрізки АА₁ і В₁С₁ у точках К і М відповідно. Доведіть, що ОК = ОМ.

Доведення.

1. Як розміщені прямі АС і М₁К₁? ( паралельні)

2. Подібність яких трикутників ви розглядали? ( ∆АВ₁С₁ і ∆ВМ₁С₁ та ∆СВ₁А₁ і ∆ВК₁А₁)

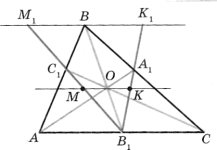3. Які рівності ви записали із подібності трикутників? ( = і = )

4. Чому дорівнює ВМ₁ і ВК₁ з рівності?  (ВМ₁ = · АВ₁  і  ВК₁ =  · СВ₁)

5. Чому дорівнює відношення ВМ₁ і ВК₁? ( 1 )

6. Яку теорему застосували? ( Менелая )

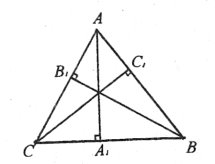
№2. Довести, що висоти трикутника перетинаються в одній точці.                                                          

                      Доведення.

   1. Подібність яких трикутників ви розглядали? ( ∆АВА₁ і ∆СВС₁, ∆АСА₁ і ВСВ₁, ∆АВВ₁ і ∆АСС₁)

   2. Які рівності ви записали із подібності  трикутників? ( = , = , = )

   3. Чому дорівнює добуток цих рівностей?                   ( 1 )

4. Яку теорему застосували? ( Чеви )