Тема.  Розв’язування  задач різними способами

Мета: вчити застосовувати знання на подібність трикутників до розв’язування задач; розвивати дослідницькі навики, уміння узагальнювати та конкретизувати властивості об’єктів, що вивчаються і застосовувати їх при вирішенні практичних завдань; формувати уміння бачити раціональні способи рішення,  пізнавальний інтерес, культуру усної мови; виховувати здатність визнавати відмінні від своїх власних ідей думки, вміння слухати і чути.

Тип уроку: застосування знань, умінь і навичок.

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання

ІІІ. Формулювання мети і завдань уроку

                                  ... часто   корисніше   розв'язати  одну  й  ту 

                                      саму  задачу трьома різними способами, ніж                             

                                           розв'язати   три – чотири різні задачі.

                                                                                 У.Соєр

ІV. Актуалізація опорних знань та вмінь

Теорема про медіани трикутника.  Усі три медіани трикутника перетинаються в одній точці, яка ділить кожну з них у відношенні     2 : 1, рахуючи від вершини трикутника.

ІV. Формування вмінь, навичок

№1. Довести теорему про медіани трикутника за подібністю трикутників.

Доведення.

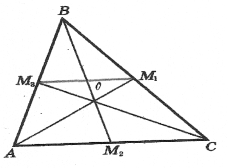     В ∆AВС  АМ₁, ВМ₂, СМ₃ медіани, які перетинаються в точці О. Проведемо М₁М₃ – середню лінію ∆AВС. За властивістю середньої лінії М₁М₃ || АС М₁АС =АМ₁М₃, М₃СА = СМ₃М₁ як внутрішні різносторонні при паралельних прямих та січні. Тоді ∆AОС ~  ∆М₁ОМ₂  за двома кутами.  Звідси АО : ОМ₁ =   СО : ОМ₃ =   АС : М₁М₃. За властивістю середньої АС = = 2М₁М₃, то АО : ОМ₁ = СО : ОМ₃ = 2 : 1. Аналогічно доводиться, що ВО : ОМ₂ = 2 : 1.

№2. Знайти радіус кола, вписаного в рівнобедрений трикутник, сторона основи якого дорівнює 16см, бічні сторони – 10см.

Розв’язання.

На рисунку в ∆AВС  АВ = ВС = 10см, АС = 16см, ВD –  висота. Точка О – центр вписаного кола. Знайдемо радіус ОF або ОD.

Спосіб 1

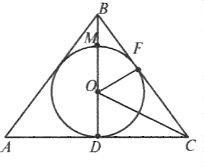  ∆ОВF ~ ∆СВD за двома кутами (В – спільний і F = D = 90°). Звідси ВF : ВD =  = ОF : СD; ОF = ВF · СD : ВD.  В рівнобедреному трикутнику за теоремою ВD є висотою, медіаною і бісектрисою, тому АD =   = DC = 8см. За властивістю дотичних   FC =   = DC = 8см,  тоді  ВF = 10 – 8 = 2 (см). Отже, ОF = 2 ·  8 : 6 = = (см).

Спосіб 2

В  ∆ВСD за властивістю бісектриси ВО : ОD = ВС : DС. Так як точка О належить ВD, то ВО = ВD – ОD.  Тоді ( 6 – ОD) : ОD =           = 10 : 8;  48 – 8 · ОD =  10 · ОD; 18 · ОD = 48; ОD = ;  ОD = (см).

Спосіб 3

За властивістю описаного трикутника, ВС –  дотична до кола, а ВD – січна, яка перетинає коло в точках М і D. За властивістю дотичної та січної маємо:  ВF² = ВМ · ВD,  де ВМ = ВD – 2 · ОD.  Отже, 4 =       = ( 6 – 2 · ОD ) · 6;  3 – ОD = ; ОD = (см).

Відповідь: ОF = ОD = (см).

V. Підсумки уроку

Я думаю, що ви отримали задоволення від свого маленького відкриття. Коли учень знаходить один спосіб розв’язання задачі – це досягнення, а коли декілька –  це успіх. Бажаю вам в майбутньому бачити декілька варіантів розв’язання не тільки математичних задач, а й життєвих проблем і неодмінно вибирати найраціональніший.

VІ. Домашнє завдання

№1. Знайдіть радіус описаного кола для рівнобедреного ∆AВС  з основою АС = 10см, бічними сторонами АВ = ВС = 13см і висотою ВD = 12см. ( за подібністю трикутників ; за властивістю хорд, які перетинаються).

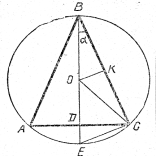Розв’язання.

 На рисунку точка О – центр описаного кола, ОК – радіус вписаного кола. Знайдемо ОВ.

 Спосіб 1

∆ОВК ~ ∆СВD за двома кутами (В – спільний і К = D = 90° ).  Звідси  ВК : ВD = ВО : ВС;  ОВ = = ВК · ВС :  ВD.  В рівнобедреному трикутнику за теоремою ВD є висотою, медіаною і бісектрисою, тому АD = DC =    = 5см. Розглянемо ∆ОВС. В трикутнику ОВ = ОС як радіус описаного кола, тому ОК за теоремою є медіаною, висотою і бісектрисою. Звідси ВК = КС = 6,5см.  Отже,  ОВ = =  = (см).

Спосіб 2

На рисунку хорди ВЕ і АС перетинаються в точці D. За властивістю хорд  АD · DC = ВD · DЕ.  Так як  АD = DC = 5см,  то    5² = 12 ( 2 · ОВ – 12 );  2 · ОВ =  ;  ОВ = ; ОВ = (см).

Відповідь: ОВ = см.