Урок 7

 

Тип урока: ОНЗ.

Тема: «Решение задач способом  приведения к единице».

Основные цели:

1) сформировать умение решать задачи на приведение к единице, записывать их условия в виде схемы, таблицы;

2) актуализировать знания смысла действий умножения и деления на равные части;

тренировать устные вычислительные навыки внетабличного умножения и деления.

Мыслительные операции, необходимые на этапе проектирования: сравнение, обобщение, классификация.

Демонстрационный материал:

1) алгоритм для решения задач на приведение к единице:

 

 

 

 

2) алгоритм для решения всех типов задач:

 

 

 

 

 

 

3) информация о животном:

Гепард — млекопитающее семейства кошачьих. Длина тела до 150 см, хвоста до 75 см. Дневной рацион – 35-40 кг мяса. Обитает в пустынях Азии (сохранился, вероятно, только в Иране) и Африки; до 1960-х гг. – на юге Туркмении (вероятно, вымер). В Индии и Передней Азии ранее использовался для охоты на антилоп. Догоняя добычу, может развивать на коротких расстояниях скорость до 120 км/ч. Малочислен. Легко приручается, в неволе размножается. В Красной книге Международного союза охраны природы и природных ресурсов (МСОП).

Раздаточный материал:

1.    листочки с текстом и схемой задачи для каждого (задание на индивидуальное затруднение):

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.    эталоны решения задач к самостоятельной работе по вариантам № 3 (а, б), стр. 19:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3) листочки с заданием на этапе актуализации:

 

 

 

 

 

 

4) Образец решения № 7, стр. 20 для этапа повторения:

 

40		18		500		5		140		68
: 4 –7 · 9	10 3 27	: 3 +9 · 5	6 15 75	: 5 –64 · 2	100 36 72	· 80 –120 : 40	400 280 7	– 60 : 40 +68	80 2 70	: 17 · 8 –32	4 32 0
27		75		72		7		70		0

 

0	7	27	70	72	75
Г	Е	П	А	Р	Д

 

Ход урока:

 

1. Мотивация к учебной деятельности:

Цель:

1) организовать актуализацию требований к ученику со стороны учебной деятельности («надо»);

2) организовать деятельность учащихся по установке тематических рамок («могу»): решение задач на умножение и деление;

3) создать условия для возникновения у ученика внутренней потребности включения в учебную деятельность («хочу») посредством анализа задачных ситуаций, близких жизненному опыту детей, и обоснования значимости математических знаний.

Организация учебного процесса на этапе 1:

На доске алгоритм решения задачи.

На доске и у каждого ребенка на листочке запись:

 

 

 

 

 

 

•      Возьмите листочки и прочитайте тексты, записанные на них. Знакомы вам такие ситуации и возникали ли они в вашей жизни? (Знакомы, возникали.)
•      Что напоминают вам эти предложения? (Тексты задач.)
•      Для чего нужно уметь решать задачи? (Для того чтобы уметь действовать в жизненных ситуациях.)
•      Какие арифметические действия следует выполнить для решения подобных задач? (Умножение и деление.)
•      Сегодня урок математики мы посвятим решению задач на действия умножения и деления, но и конечно узнаем, что-то новое. Как вы это будете делать? (Узнаем, чего мы ещё не знаем, и сами будем открывать новые знания.)

Учитель открывает часть темы на доске: Задачи.

2. Актуализация знаний и фиксация затруднения в пробном действии.

Цель:

1) организовать актуализацию изученных способов действий, достаточных для построения нового знания: актуализировать способы решения  простых задач на смысл действия умножения и деления; тренировать навык  внетабличного умножения и деления;

2) зафиксировать актуализированные способы действий в речи;

3) зафиксировать актуализированные способы действий в знаках (эталоны);

4) организовать обобщение актуализированных способов действий;

5) организовать актуализацию мыслительных операций, достаточных для построения нового знания: анализ, синтез, обобщение, классификацию;

6) мотивировать к пробному учебному действию («надо» – «могу» – «хочу»);

7) организовать самостоятельное выполнение пробного учебного действия: решение задачи нового вида;

8) организовать фиксацию индивидуальных затруднений в выполнении учащимися пробного учебного действия или в его обосновании.

Организация учебного процесса на этапе 2:

1) Актуализация способов решения простых задач на умножение и деление.

а) Решите задачи устно. (Мы не можем решить задачи, так как не хватает данных.)

•      Каким одним общим данным нужно дополнить условия обеих задач для того, чтобы ответить на вопросы? (Нужно указать, сколько стоит 1 кг картофеля.)
•      Сколько может стоить 1 кг картофеля? (…)

Учитель записывает варианты именованных чисел, предложенные детьми: 5 рублей, 10 рублей, 8 рублей; 12 рублей.

•      Выберите из предложенных чисел подходящие для решения обеих задач. (8 или 12 рублей, так как 48 делится на оба этих числа.)
•      Дополните условия обеих задач данным – 8 рублей.

б) Учитель дополняет записи на доске, а дети на листочках.

 

 

 

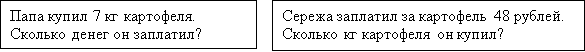
1 кг – 8 рублей.

•      Дополните схемы задач. Какое данное не отмечено на схеме? (Стоимость 1 кг картофеля.)
•      Как это обозначить на схемах. (В первой задаче провести дугу над единичным отрезком и записать сверху 8 рублей; во второй схеме надо отметить единичный отрезок и написать сверху 8 рублей.)
•      Какой длины должен быть единичный отрезок на второй схеме? (Точно такой же, как и в первой.)
•      Почему? (Потому что это одно и то же данное.)
•      Выделите единичный отрезок в каждой схеме красным цветом.

в) – Запишите решение задач на карточке.

Дети выполняют работу. По ее окончании двое учащихся записывают решение на доске:

8 · 7 = 56 (руб.) 48 : 8 = 6 (кг)

•      Почему первую задачу решили действием умножения? (Потому что по 8 рублей взяли 7 раз.)
•      В чем смысл действия умножения? (Взять одинаковое слагаемое несколько раз.)
•      Почему выбрали такой порядок множителей? (Потому что по 8 взяли 7 раз.)
•      Почему для решения второй задачи выбрали действие деление? (Потому что надо было узнать, сколько раз по 8 рублей содержится в 48 рублях.)
•      К какому типу задач на деление она относится? (Деление по содержанию.)
•      Придумайте взаимно обратную задачу с делением на равные части. (Сережа купил 6 кг картофеля и заплатил 48 рублей. Сколько стоит 1 кг картофеля?)
•      Молодцы! Посмотрите на решённые задачи. Что в них общего? (Это простые задачи, они решаются одним действием: умножением или делением, похожи сюжетом, одно из числовых данных одинаковое.)
•      Что вы сейчас повторили? (…)
•      Какое задание будет вам сейчас предложено? (…)
•      Что вам поможет решение пробного задания? (…)

2) Пробное задание.

•      Возьмите листочки, лежащие на ваших столах. Прочитайте задачу.

Учащиеся работают с раздаточным материалом Р–1.

•      Заполните схему. Какой отрезок соответствует условию «4 шапочки»? (Меньший.)
•      Как на схеме отмечено, что шапочки одинаковые? (Отрезок разделен на четыре равные части.)
•      Почему около второго отрезка я записала: 6 ш. – ? м.? (Второй отрезок обозначает количество мотков шерсти, которое идет на изготовление 6 шапочек. Это количество надо узнать.)

Учитель на доске со слов детей заполняет схему, дети — на листочках.

 

 

 

 

 

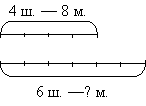
•      Что нового в этой задаче? (Надо найти, сколько пойдёт шерсти на 6 ш., а не на 1 ш.)
•      Теперь попробуйте самостоятельно ответить на этот вопрос.

На выполнение задания отводится 2 минуты.

•      Кто не получил ответ? (…)
•      Чего вы не смогли сделать? (Мы не смогли решить задачу, в которой надо найти, сколько мотков шерсти пошло на 6 шапочек.)
•      Какие ответы получились у тех, кто решил задачу? (…)

Учащиеся называют разные варианты ответов.

Учитель предлагает учащимся с разными вариантами ответов записать свое решение задачи на доске. Остальные учащиеся определяют свою позицию в записи решений, например, поднятием руки.

•      Как доказать, какое решение верное? (Не знаем. У нас нет способа решения таких задач.)
•      В чём затруднение у тех, кто решил задачу? (Мы не ожжем доказать, чьё решение верно.)

 

3. Выявление места и причины затруднения.

Цель:

1.                организовать восстановление выполненных операций;
2.                организовать фиксацию места (шага, операции), где возникло затруднение;
3.                организовать соотнесение своих действий с используемыми эталонами (алгоритмом, понятием и т.д.).

На этой основе организовать выявление и фиксацию во внешней речи причины затруднения – тех конкретных знаний, умений или способностей, которых недостает для решения исходной задачи и задач такого класса или типа вообще.

Организация учебного процесса на этапе 3:

•      Возьмите листочки с предыдущими задачами и обратите внимание на схемы всех трех задач. Чем они похожи? (В схемах всех трех задач есть равные единичные отрезки.)
•      Чем эта задача отличается от предыдущих? (В первых двух задачах было известно значение единичного отрезка, а в третьей задаче — неизвестно.)
•      Что обозначает единичный отрезок на схеме к третьей задаче? (Количество мотков шерсти, израсходованных на изготовление одной шапки.)
•      Можно ли решить последнюю задачу, не зная сколько мотков шерсти пошло на одну шапку? (Нет, так как не сможем ответить на вопрос задачи.)
•      Почему вы не можете решить последнюю задачу? (У нас нет способа для решения таких задач.)

 

4. Построение проекта выхода из затруднения.

Цель:

Организовать построение проекта выхода из затруднения:

1. учащиеся ставят цель проекта: построить способ изображать часть множества;
2. учащиеся уточняют и согласовывают тему урока;
3. учащиеся определяют средства (алгоритмы, модели, справочники и т.д.).
4. учащиеся формулируют шаги, которые необходимо сделать для реализации поставленной цели.

Организация учебного процесса на этапе 4:

•      В этом случае в математике говорят, что значение искомой величины нужно привести к единице.

Учитель записывает на доске: приведение к единице.

•      Итак, какова же цель сегодняшнего урока? (Построить способ решения задач методом приведения к единицы и научиться решать задачи на приведение к единице.)
•      Сформулируйте тему урока. (Задачи на приведение к единице.)

Учитель окончательно оформляет тему урока: «Задачи на приведение к единице».

•      Что вы будете использовать при построении способа? (Схему, алгоритм решения задач.)
•      Как вы будете действовать? (Проанализируем условие задачи, решим данную задачу, построим общий способ решения задач, приведение к единицы.)

 

5. Реализация построенного проекта.

Цель:

1) организовать реализацию построенного проекта в соответствии с планом;

2) организовать фиксацию нового способа действия в речи;

3) организовать фиксацию нового способа действия в знаках (с помощью эталона);

4) организовать фиксацию преодоления затруднения;

5) организовать уточнение общего характера нового знания (возможность применения нового способа действий для решения всех заданий данного типа).

Организация учебного процесса на этапе 5:

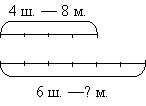
Учитель восстанавливает сюжет задачи по схеме:

•      Что известно в задаче? (Количество шапок – 4 и 6, количество мотков шерсти, израсходованных на четыре шапки – 8)
•      Что неизвестно? (Количество мотков шерсти, которые понадобятся для 6 таких же шапочек.)
•      Что необходимо знать, чтобы ответить на главный вопрос задачи? (Количество мотков шерсти, которые понадобятся для изготовления одной шапки.)
•      Известна вам эта величина? (Нет.)
•      Отметьте на схеме эту неизвестную величину. Что надо дописать? (Надо поставить знак вопроса под делением первого отрезка: он означает, что мы не знаем, сколько мотков шерсти пошло на 1 шапку.)

Учитель дописывает вопрос в схему на доске, выделяет красным цветом единичные отрезки и проводит пунктирные линии.

•      Сколько действий в задаче? (Два.)
•      Как определили? (По количеству вопросов на схеме.)

 

 

 

 

 

 

•      Какое действие выполните сначала? (8 мотков разделим на 4 равные части. Узнаем, сколько мотков пошло на одну шапку.)
•      Запишите первое действие в решении задачи.

Один ученик записывает первое действие в решении задачи на доске, остальные — на

листочках:

8 : 4 = 2 (м.) – пошло на 1 шапку.

•      Сможете теперь узнать, сколько мотков шерсти пойдет на 6 шапок? (Да. Для этого надо по 2 мотка взять 6 раз, то есть выполнить действие умножения.)
•      Запишите второе действие в решении задачи.

Другой ученик записывает второе действие в решении задачи на доске, остальные — на

листочках:

2 · 6 = 12 (м.) – пошло на 6 шапок.

•      Почему вы 2 умножили на 6, а не наоборот? (Мы взяли два мотка для одной шапки и повторили их слагаемым для 6 шапок.)
•      Запишите выражение к задаче: что сделали сначала, что — потом.

Один ученик работает у доски с объяснением, остальные — на листочках:

(8 : 4) · 6 = 12 (м.)

•      Ответили вы на вопрос задачи? (Да.)

Учитель обращает внимание детей на записи разных решений этой задачи на доске.

•      Кто решил задачу так же?
•      Как нужно действовать, чтобы вы смогли решить любую задачу такого вида? (Нужно составить алгоритм решения задач такого вида.)
•      Как решать задачи на приведение к единице? (Сначала надо искомую величину привести к единице.)
•      Каким действием? (Делением.)
•      Какой второй шаг? (Ответить на главный вопрос задачи, выполнив умножение.)

Учитель выставляет на доске карточки с шагами алгоритма, которые дети проговаривают хором.

 

 

 

 

Учитель стирает схему задачи на доске, оставляя следующую запись:

4 ш. – 8 м.

6 ш. – ? м.

•      Можно ли по этой записи рассказать задачу? (Да.)
•      Эта запись называется таблицей. Удобно пользоваться такой записью? (Да.)
•      Почему? (Не надо чертить схему, занимает мало места, быстрее.)
•      Сравните эту запись со схемой на ваших листах. Что необходимо добавить в краткую запись задачи. (Вопрос: сколько мотков шерсти пошло на одну шапку?)

Учитель знакомит детей с краткой записью задачи:

4 ш. – 8 м.

6 ш. – ? м.

1 ш. – ? м.

•      Вы достигли цели? (Мы открыли способ, теперь надо научиться решать такие задачи.)

6. Первичное закрепление с проговариванием во внешней речи.

Цель:

организовать усвоение детьми нового способа действий при решении данного класса задач с их проговариванием во внешней речи:

- фронтально;

- в парах или группах.

Организация учебного процесса на этапе 6:

1.    № 1, стр. 19.

Один ребенок читает вслух: «Три книги стоят 42 рубля. Сколько рублей стоит 5 таких книг?»

Ученики комментируют ход решения задачи, пользуясь выведенным алгоритмом. И общим алгоритмом решения всех задач, который учитель помещает на доску.

 

 

Учащиеся по очереди выходят к доске и выполняют задание, комментируя шаги алгоритма.

•      Называю известные и неизвестные величины. Известно, что три книги стоят 42 рубля. Надо узнать, сколько стоят 5 книг.
•      Составляю таблицу:

3 кн. – 42 руб.

5 кн. – ? руб.

1 кн. – ? руб.

•      Привожу искомую величину к единице, для этого стоимость трех книг разделю на их количество: 42 : 3 = 14 (руб.) – стоит 1 книга.
•      Найду значение величины. Для этого стоимость одной книги умножу на количество книг:

14 ∙ 5 = 70 (руб.).

•      Записываю решение этой задачи выражением 42 : 3 ∙ 5 = 70 (руб.).

На доске и в тетрадях у учеников появляются записи:

3 кн. – 42 руб. 1) 42 : 3 = 12 (руб.) – стоит одна книга.

5 кн. – ? руб. 2) 12 · 5 = 60 (кг)

1 кн. – ? руб. (42 : 3) · 5 = 60 (кг)

 Ответ: 60 рублей стоят 5 книг.

•      У вас отлично получается! Решим ещё одну задачу.

2.    № 2, стр. 19.

Дети работают самостоятельно, комментируя выполнение задания друг другу, пользуясь алгоритмом. Одна пара работает у доски, и по её решению проводится проверка. Учитель при необходимости консультирует.

•      Теперь вы сможете сами решать такие задачи, пользуясь алгоритмом? (Сможем.)

Оформление задач аналогично:

7 ящ. – 56 кг 1) 56 : 7 = 8 (кг) – в одном ящике.

10 ящ. – ? кг 2) 8 · 10 = 80 (кг)

1 ящ. –  ? кг (56 : 7) · 10 = 80 (кг)

 Ответ: 80 кг в 10 ящиках.

- Что теперь необходимо сделать? (Проверить, сможем ли самостоятельно справиться с такой задачей.)

 

7. Самостоятельная работа с самопроверкой по эталону.

Цель:

1) организовать самостоятельное выполнение учащимися типовых заданий на новый способ действия;

2) организовать соотнесение работы с эталоном для самопроверки;

3) организовать вербальное сопоставление работы с эталоном для самопроверки*

4) по результатам выполнения самостоятельной работы организовать рефлексию деятельности по применению нового способа действия.

Организация учебного процесса на этапе 7:

I вариант –  № 3 (а), стр. 19

II вариант –  № 3 (б), стр. 19

•      Решите задачи самостоятельно по вариантам.

На выполнение задания отводится 3 минуты. Учитель сначала может дать детям время для записи краткого условия задачи в виде таблицы и сразу проверить ее, затем дать время для записи решения задачи по действиям и выражением.

Самопроверка проводится по эталону для самопроверки.

•      Проверьте себя по эталону. В чём он вам поможет? (Проследить ход выполнения задания по шагам и выяснить причину ошибки, если она есть.)

Дети проверяют свою работу по эталону.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

•      Какие возникли затруднения? (…)
•      Скажите, в чём причина ошибки? Назовите соответствующий шаг. (…)
•      У кого не всё получилось? Поставьте себе «?».
•      Если вы сделали задание правильно, то поставьте себе «+».

Дети оценивают себя, выставляя на полях «+»; «?».

8. Включение в систему знаний и повторение.

Цель:

1) тренировать вычислительные навыки;

2) повторить темы: «Множество и его элементы», «Подмножество», «Знаки  и ».

Организация учебного процесса на этапе 8:

1) Множество и его элементы. Подмножество.

•      Давайте проверим, кто сегодня был внимателен. Рассмотрим множество задач, которое вы решали на уроке. Перечислите их. (Две простые задачи в начале урока…)

Если дети затрудняются с ответом, учитель указывает на записи задач на доске.

•      Обозначим их задачами 1 и 2: • 1      • 2
•      Затем вы решали задачу… (На листочках.)
•      Обозначим её буквой Л: • Л

Дети рисуют в тетради, учитель на доске.

•      Следующие задачи легко вспомнить, если заглянуть в учебник. (Задачи № 1, № 2, № 3 (а), № 3 (б).)

 

 

•      Обозначьте их соответственно:

 

 

 

 

 

 

 

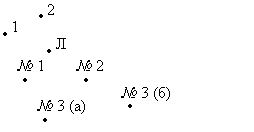
Дети рисуют в тетради, учитель на доске.

•      Постройте диаграмму Венна данного множества.

Дети обводят замкнутой линией точки, обозначающие задачи

•      Запишите, что элементы, обозначающие задачи самостоятельной работы, принадлежат множеству С. (№ 3 (а)  С, № 3 (б)  .)

Один ребенок работает у доски, остальные — в тетрадях.

 

 

 

 

 

 

 

 

•      Как называются задачи нового типа, с которыми вы познакомились на сегодняшнем уроке? (Задачи на приведение к единице.)
•      Выделите их на диаграмме отдельным множеством и обозначим буквой Р.

 

 

 

 

 

 

 

 

 

•      Что вы можете сказать о множествах С и Р? (Множество Р является подмножеством множества С.)
•      Запишите это. (Р  С.)
•      Когда используются знаки  и ? (Знак  ставится между элементом и множеством, а знак  — ставится между множествами.)
•      Вы работали с множеством задач, а теперь потренируемся в решении примеров.

 

2) Тренинг устных вычислительных навыков.

№ 7, стр. 20.

Учащиеся выполняют задание самостоятельно в учебниках. На выполнение задания дается 4 минуты. Проверяют работу по образцу. После проверки исправляют ошибки.

Учитель вывешивает на стенде и читает энциклопедическую справку об этом животном.

Если есть время, можно предложить детям придумать задачи про гепарда. Дети могут предложить такие задачи:

«Двум гепардам на день понадобится 80 кг мяса. Сколько килограммов мяса понадобится пяти таким гепардам?»

Можно решить эту задачу в рабочих тетрадях. Ребенок, придумавший задачу, решает её на доске.

2 г. – 80 кг 1) 80 : 2 = 40 (кг) – одному гепарду;

5 г. – ? кг 2) 40 · 5 = 200 (кг).

1 г. – ? кг 80 : 2 · 5 = 200 (кг).

 Ответ: 200 кг мяса понадобится пяти гепардам.

Учитель предлагает дома еще поразмышлять, написать задачи на отдельных листочках, а завтра предложить одноклассникам решить их.

9. Рефлексия учебной деятельности на уроке.

Цель:

1) организовать фиксацию нового содержания, изученного на уроке;

2) организовать рефлексивный анализ учебной деятельности с точки зрения выполнения требований, известных учащимся;

3) организовать оценивание учащимися собственной деятельности на уроке;

4) организовать фиксацию неразрешённых затруднений на уроке как направлений будущей учебной деятельности;

5) организовать обсуждение и запись домашнего задания.

Организация учебного процесса на этапе 9:

•      Какие цели вы ставили перед собой? (Построить способ решения задач на приведение к единице и научиться их решать.)
•      Достигли вы цели? (Да.)
•      Докажите? (…)
•      Что вам помогло в решении задач? (Алгоритм решение задачи, таблица, схема.)
•      У кого были затруднения?

Дети поднимают руку.

•      Смогли вы справиться с затруднениями? (Да.)
•      Поднимите руку те, кто считает, что сегодня вы были участниками учебной деятельности. (…)
•      Почему вы так считаете?

Дать некоторым учащимся высказаться.

•      Как вы думаете, следует ли вам потренироваться в решении задач на приведение к единице? (Да.)
•      Поэтому дома решите задачу способом приведения к единице, запишите домашнее задание.

 

Домашнее задание:

записать новый алгоритм в тетрадь для теории;

 № 10, 11, стр. 21;

☺ № 5, 6, стр. 20 (придумать задачу на приведение к единице про гепарда).