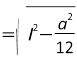Урок "Розв’язування задач з теми "Піраміда"

Дата: _____________

Тема уроку: Розв’язування задач

Мета: продовжити формування поняття піраміди, властивостей її елементів, формувати вміння їхнього застосування до розв’язування задач; формувати вміння виявляти особливості конструкції піраміди;

           розвивати просторову уяву та уявлення, уважність, здатність до узагальнення та систематизації фактичного матеріалу;

           виховувати культуру мовлення, культуру математичних записів, графічну культуру, охайність у веденні записів, наполегливість, старанність.

Тип уроку: формування вмінь та навичок.

Обладнання : дошка, крейда, презентація з ілюстраціями до математичного диктанту, текстами задач, домашнім завданням.

Хід уроку

І Організаційний момент: привітання, перевірка готовності класу до роботи; повідомлення теми та дидактичної мети уроку.

ІІ Актуалізація опорних знань

З метою актуалізації опорних знань проводимо математичний диктант на листочках з подальшим обговоренням відповідей.

Математичний диктант: На екрані висвітлюємо 5 пронумерованих малюнків:

Пропонуємо учням дати відповіді на питання:

№ з/п	Варіант № 1		Варіант № 2
1	Запишіть номер малюнка, на якому зображено
	правильну чотирикутну піраміду		правильну трикутну піраміду
2	Перелічіть бічні ребра цієї піраміди		Перелічіть бічні грані цієї піраміди
3	Сформулюйте і запишіть означення
	висоти піраміди		апофеми
4	Дано: піраміда з апофемою ℓ і стороною основи а. Знайти висоту
	правильної чотирикутної піраміди		правильної трикутної піраміди.
5	За тими самими даними, знайти повну поверхню піраміди
	правильної чотирикутної піраміди	правильної трикутної піраміди.
6	Знайти двогранний кут при ребрі основи
	правильної чотирикутної піраміди		правильної трикутної піраміди.
7	Назвати і записати кут між бічним ребром і площиною основи
	правильної чотирикутної піраміди		правильної трикутної піраміди.
8	За тими самими даними знайти площу перерізу піраміди площиною, проведеною через середину висоти
	правильної чотирикутної піраміди		правильної трикутної піраміди.

Збираємо роботи, обговорюємо відповіді, проводимо корекцію знань:

№ з/п	Варіант 1	Варіант 2	Кількість балів за правильну відповідь
1	Мал. 4	Мал. 2	1
2	SA, SB, SC, SD	ΔABS, ΔBCS, ΔACS	1
3	Висота — це перпендикуляр, опущений з вершини піраміди на її основу	Апофема — це висота бічної грані правильної піраміди, проведена з вершини піраміди	1
4	h	h	2
5	S=a2+2al	hal	2
6	∠SMO = 2l	∠SLO = 6l	2
7	∠SAO, ∠SBO, ∠SCO, ∠SDO	∠SAO, ∠SBO, ∠SCO	1
8	S	h	2

Звертаємо увагу на те, що для розв’язання завдань 4 та 6 потрібно розглянути одні й ті самі прямокутні трикутники:

Відповідали біля дошки: _______________________

_______________________

_______________________

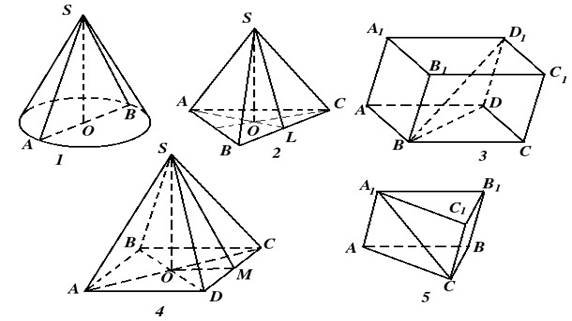
______________________ ВАРІАНТ 1

У трикутнику SOM SO = h — шукана висота, ОМ = a

 ­ радіус кола вписаного в квадрат, тоді за

2

теоремою Піфагора h , і за означенням косинуса гострого кута прямокутного

трикутника, знаходимо: cosM=^OM             тому ∠SMO = _arccos ^a       .

                                                                                           SM                                                   2l

ВАРІАНТ 2

 У трикутнику SOL SO = h — шукана висота, ОL =  ^a√3 ­ радіус кола вписаного в 6

правильний трикутник, тоді за теоремою Піфагора , h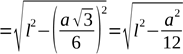 і за

a тому ∠SLO = arccos √3 . 6l Фронтальне опитування:
•                 • • •                 • •                 • •	Що називається двогранним кутом? Що є мірою двогранного кута? Що називається косинусом, синусом, тангенсом гострого кута прямокутного трикутника? Що називається кутом між похилою і площиною?  Записати формули площі квадрата, правильного трикутника. Назвати кути між бічними ребрами і площиною основи? Що називається бічною поверхнею піраміди? Повною поверхнею піраміди? Які є способи обчислення бічної поверхні правильної	Активно працювали: ___________________   ___________________ ___________________ __________________ ___________________

означенням косинуса гострого кута прямокутного трикутника, знаходимо: cosL=^OL , SL

піраміди? (2 способи: за означенням: l , та за теоремою про площу ортогональної проекції многоранника :

S

S_б= осн cosϕ

ІІІ Розв’язування задач Евристична бесіда:

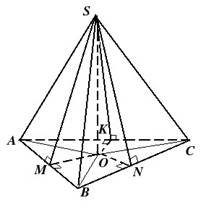Зупинимося детально на способі обчислення бічної поверхні, який ґрунтується на теоремі про площу ортогональної проекції. Чому можна використати цю формулу?

•         Бічна поверхня ортогонально проектується на основу і усі двогранні кути при основі рівні.

Розглянемо піраміду, яка не є правильною, наприклад, таку, в основі якої лежить різносторонній трикутник зі сторонами 13, 14, і 15 см та усі бічні грані якої утворюють рівні кути α = 60⁰ з площиною основи. Знайдемо висоту піраміди та її бічну поверхню.

Зобразити піраміду в зошитах та на дошці, позначити на малюнку двогранні кути. Що є мірою цих кутів?

•         Лінійні кути.

Як їх зобразити? Між якими лінійними елементами вони вимірюються?

•         Це кут між висотою бічної грані та її проекцією на площину основи.(∠SMO= ∠SNO = ∠SKO) Якщо двогранні кути рівні, за умовою, якими є висоти бічних граней? Їхні проекції?

•         Рівними (SM = SN = SK, як відповідні сторони рівних прямокутних трикутників

ΔSON=ΔSOM=ΔSOK ; MO = NO = KO, як

проекції рівних похилих, проведених з однієї точки) Чим є т.О. ­ основа висоти?

•         Т. О — рівновіддалена від сторін основи і є центром вписаного кола.

•         r₌ ^2S  , площу можна знайти за формулою Герона, висоту — з прямокутного a+b+c трикутника, наприклад, ΔSON за означенням тангенса гострого кута: tgα₌ ^SO

ON S=84 см², r=4см, SO=ON tgα=r tg60⁰=4√3см.

Чим є трикутники ВОС, АОВ і АОС для бічних граней BSC, ASB i ASC відповідно?

•         Ортогональними проекціями цих трикутників.

Яке співвідношення між їхніми площами?

Sпроекції

•         SΔ= cosα

Як знайти площу бічної поверхні?

Sб=SΔASC+SΔASB+SΔBSC=ScosΔAOCα+ScosΔAOBα+SΔBOC = 1 (SΔAOC+SΔAOB+SΔBOC)=SΔABC

Sб= 84 0=168см2 cos60

Таким чином ми з’ясували:

Якщо усі бічні грані піраміди утворюють рівні кути з площиною її основи, то:

•         вершина піраміди проектується в центр кола, вписаного в основу піраміди; • висоти бічних граней піраміди — рівні;

S^осн

•         бічну поверхню піраміди можна обчислити за формулою S_б= . cosϕ Задача:

Основа піраміди — ромб зі стороною а і гострим кутом α.                  Розв’язував

Знайти висоту і бічну поверхню піраміди, якщо усі двогранні ____________________________________________ кути при ребрах основи дорівнюють ϕ. _____________________

S_o.

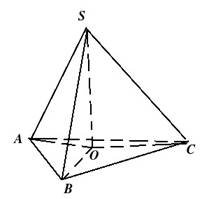
Евристична бесіда. Куди буде проектуватися висота піраміди, якщо її бічні ребра утворюють рівні кути з площиною основи?

Як знайти кут між бічним ребром і площиною основи?

•         Бічне ребро є похилою до основи.

•         Кутом між похилою і площиною називається кут між похилою і її проекцією на площину основи.

•         Проекцією бічного ребра є відрізок, що сполучає відповідну вершину основи та основу висоти.

•         АО, ВО, СО — проекції SA, SB i SC відповідно. Прямокутні трикутники  SAО = SBО = SCО, і, отже, бічні ребра рівні (як гіпотенузи рівних трикутників) і т. О  ­ рівновіддалена від вершин трикутника (бо АО = ВО = СО, як проекції рівних похилих, проведених з однієї точки) і є центром кола, описаного навколо цього трикутника.

Висновок

Рівні бічні ребра піраміди утворюють рівні кути з площиною її основи; вершина такої піраміди  проектується в центр кола, описаного навколо її основи.

Задачі:

Основою піраміди є рівнобедрений прямокутний Розв’язав

трикутник з гіпотенузою 8 см. Знайти висоту та бічні ___________________________ ребра піраміди, якщо вони утворюють кути, рівні 30⁰ __________________________

з площиною основи піраміди. ___________________________ Основависоти−серединагіпотенузи, Нсм, bсм.

Основа піраміди — рівнобедрений трикутник з основою а і кутом при вершині α. Усі бічні ребра піраміди рівні b. Знайти висоту піраміди.

          R         ^a      , занаслідком зтеор.синусів;                Розв’язав________________________

_______________________________

H, занаслідком зтеор.Піфагора                                         _______________________________

______________________________

ІV. Підсумок уроку

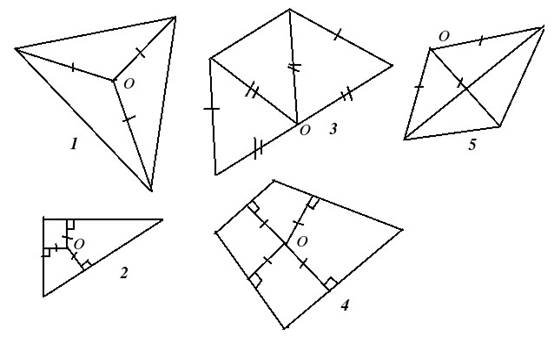Розв’язування усних вправ (малюнки на екрані): на малюнках 1 ­ 5 зображено ортогональні проекції основ пірамід та зазначено положення основи висоти — т. О. Поясніть особливості будови цих пірамід.

Відповідали:

_____________

______________

______________

______________ Оцінки за урок:

________________

________________

________________

__________________

Повідомлення домашнього завдання:

•        вивчити конспект,

•        повторити параграф 16, формули радіусів вписаних та описаних кіл їхнє положення, умови, за яких чотирикутники можна вписати в коло та описати навколо кола;

•        розв’язати № 3 с.267, № 137 с.262, № 156* с. 263.