Урок-семінар "Похідна та її застосування" з алгебри і початків аналізу в 11 класі

Мета: перевірити сформованість в учнів умінь встановлювати характер зміни функції за знаком похідної; виявляти точки, підозрілі на екстремум; використовувати поняття похідної для дослідження властивостей функцій; застосовувати метод диференціального числення до розв'язування прикладних задач; розвивати пізнавальний інтерес, навички колективної праці та самоконтролю.

1. Організаційний момент
2. Історичні відомості.

Вона на вигляд недолуга:

Штришок маленький, та  й усе.

 Але яку значну потугу

Цей ледь помітний знак несе!

ГЕОМЕТРИЧНИЙ ЗМІСТ ПОХІДНОЇ

Алгебра – це  лише  писана геометрія,

 а геометрія — зображена алгебра

С.Жермен

Пряме не може бути кривим, а криве — прямим. І все-таки диференціальне числення, всупереч усім протестам здорового людського розуму, порівнює за певних умов пряме й криве і досягає успіху.

Застосування похідної в геометрії пов'язане із задачею про дотичну до кривої в певній точці. Характерною властивістю будь-якої кривої є її напрям, який змінюється від точки до точки. Цей напрям характе­ризується напрямом дотичної до кривої в цій точці. Але що таке дотична?

Існування похідної функції f(х) в точці х₀ рівносильне існуванню дотичної (не вертикальної) у даній точці графіка, кутовий коефіцієнт якої дорівнює f'(х). Це і є геометричний зміст похідної.

ПОХІДНА У ФІЗИЦІ Й ТЕХНІЦІ

Алгебра і геометрія — єдині країни,

де панують тиша і мир.

М. Ань'єзі

Поняття похідної виникло у XVII ст. у зв'язку з необхідністю розв'язати деякі математичні і фізичні задачі. Задачу про побудову дотичної розв'язав Г.Лейбніц, про визначення миттєвої швидкості під час прямолінійного нерівномірного руху — І.Ньютон, який прийшов до поняття похідної, виходячи з положень механіки. Результати своїх досліджень І.Ньютон виклав у трактаті «Метод флюксій», опублі­кованому в 1736 р. Учений називав похідну флюксією, а саму функцію — флюентою.

Похідна — це швидкість зміни функції. Нехай матеріальна точка рухається вздовж координатної прямої х за законом х = х(і). Тоді похідна від координати за часом у даний момент є швидкістю руху в цей момент часу. У цьому й полягає її механічний зміст.

Поняття похідної як швидкості зміни функції використовується під час означень багатьох фізичних величин. Наприклад, похідна швидкості руху за часом є прискорення, похідна величини заряду за часом є сила струму; похідна потоку магнітної індукції за часом є електрорушійна сила індукції; похідна роботи за часом є потужність.

ЗАСТОСУВАННЯ ПОХІДНОЇ ДО ДОСЛІДЖЕННЯ ФУНКЦІЇ

Алгебра щедра. Дуже часто вона дає більше,

 ніж у неї просять.

Ж. Д'Аламбер

Іноді може виникнути запитання: для чого потрібна похідна? Може її видумали вчені тільки для того, щоб похизуватися знаннями про неї перед іншими людьми? А може це «гола» теорія — і все?

Як ми переконалися, похідна широко використовується у фізиці. Крім того, з її допомогою проводять дослідження функції на зростання і спадання, екстремуми, найбільше і найменше значення. Наприклад, якщо f'(х) > 0 в кожній точці інтервалу І, то функція f(х) зростає на І; якщо  f'(х) < 0 в кожній точці інтервалу І, то функція спадає на І. А як поводить себе функція в точках, в яких похідна не існує або дорівнює 0, тобто в критичних точках, і що є необхідною умовою екстремуму?

Умова існування екстремуму в точці така:

Якщо в критичній точці х₀ похідна змінює знак з «плюса» на «мінус», то х₀ — точка максимуму, а якщо змінює знак з «мінуса» на «плюс», то х₀ є точкою мінімуму.

3.    Актуалізація опорних знань учнів.

 Учням пропонуються запитання.

1.             Як пов'язані між собою монотонність функції та її похідна?
2. Що відбувається з похідною в точці її екстремуму?
3. В яких точках неперервні функції:

а)многочлен

б) дробово-раціональна?

4. Вказати проміжки неперервності функції: 

а) f(х) = х³-2х+4

б) f(х)= 9х

IV. Узагальнення та систематизація вмінь та навичок учнів

Учитель. Дуже часто ми зустрічаємось із практичними задачами, розв'язування яких зводиться до застосування похідної. У Л. М. Толстого є оповідання «Чи багато людині землі потрібно?».

Задача. Роками мріяв селянин Пахом про власну землю. Довго гроші збирав, відмовляючи собі в усьому! І ось, нарешті, зібрав заповітну суму. Старшина поставив йому таку умову:

— Скільки за день землі обійдеш, уся твоя буде за 1000 крб, але коли до заходу сонця не повернешся на місце, з якого вийшов, — втратив ти свої гроші.

Тільки зійшло сонце, вирушив Пахом від мітки. Пройшов верст 10 і звернув круто вліво. Пройшов по цій стороні ще більше, верст 13, загнув другий кут. Третьою стороною пройшов усього 2 версти, глянув на сонце, а воно вже низенько, а до мітки ще верст 15 буде. І став напрямки поспішати. Біг, біг, прибіг до мітки і впав... мертвий.

Запитання

1. Який шлях подолав Пахом? Яку площу оббіг?
2. Яким шляхом було б краще піти селянину, щоб, пройшовши тих же 40 верст, обійти найбільшу площу?

Розв'язання

1спосіб.

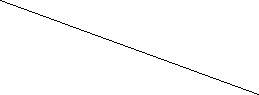
 Шлях, пройдений Пахомом, дорівнює периметру трапеції АВСD. Р = 10 + 13 + 2 + 15 = 40 (верст)

Площа ділянки землі: S = (10 + 2) :2 • 13 = 78 (кв. верст)

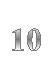
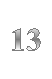
2 спосіб.

Нехай селянин ішов по прямокутнику, периметр якого Р = 40верст. Якщо АВ = х верст, ВС = (20 - х) верст.

Знайдемо площу прямокутника АВСD:

S(х) = х(20 -х) = 20х-х², х є (0; 20)

Дослідимо функцію на екстремум. Знаходимо критичні точки функції:

S'(х)=20-2х, 20-2х = 0, тобто х = 10/

 Коли х<10, то S'(х) > 0 і функція S(х) зростає. Коли х>10, то 8'(х) < 0 і функція S(х) спадає.

Отже, точка х=10 є точкою максимуму і mах S(х) = S(10) = 100 верст

                                                                                                                        [0; 20]

Тоді АВ=10 верст, ВС=20 - 10 = 10 верст.

Відповідь. З усіх прямокутників з периметром Р=40 верст найбільшу площу має квадрат зі стороною 10 верст. Рухаючись по квадрату, селянин пройшов би площу 100 квадратних верст.

Задача 2. У країні Меланхолії виникла епідемія депресії, яка розповсюджується так, що відсоток р захворівших залежить від часу t (в добах) так:

р= 0,005(12t²- t³), де  0≤t≤12.

1. Скільки відсотків мешканців захворіє до кінця другої доби?

2. Скільки днів відсоток захворівших буде збільшуватися?

3. Починаючи з якої доби епідемія почне спадати?

4. На який день відсоток захворюваності досягне максимуму? Дана прикладна задача є задачею на застосування похідної до

дослідження функції, яка відіграє роль її математичної моделі, на моно­тонність та екстремум. Її розв'язування вимагає наявності в учнів знань про достатні умови зростання та спадання функції та достатньої умови існування екстремуму функції в точці.

Відповідь на перше запитання одержується дуже легко, а саме: знаходиться значення функції р(t), якщо t=2 -  воно дорівнює 0,2 %. Для відповіді на наступні запитання учні знайдуть похідну функції

р= 0,005(24t- 3t²),

стаціонарні точки t=0 та t=8. Оскільки час t>0, то між кінцями відрізка [0; 12] існує єдина стаціонарна точка t=8. При переході через цю точку похідна змінює знак з «плюса» на «мінус», а отже, функція в ній має максимум і через єдиність стаціонарної  точки функція досягає в цій точці найбільшого значення.

Тому перші 8 діб епідемія буде зростати, починаючи з 9-ї доби - почне спадати, а відсоток захворівших досягне максимуму на 8-му добу.

Самостійна робота

Задача. Лижник, спускаючись з гірки, рухається за законом S(t)=0,5t²-t. Знайти швидкість і прискорення лижника в момент часу  t= Зс, якщо відстань вимірюється в метрах/

5. Підсумок уроку

VІ. Домашнє завдання