Урок "Симетрія відносно точки".

Тема. Симетрія відносно точки

Мета: сформувати поняття про симетрію відносно точки, вчити будувати фігури симетричних даним відносно точки; розвивати спостережливість, увагу, графічну культуру; виховувати відповідальність, спонукати до самостійного здобуття знань; отримати уявлення про прояви симетрії в природі, різних галузях науки й людської діяльності;   розв’язувати  елементарні задачі на поняття симетрії.

Типи уроків: засвоєння нових знань, комбіновані.

Бути прекрасним означає бути симетричним і пропорційним

Платон

І. Організаційний момент

 (Учитель запрошує поміркувати над епіграфом уроку, просить учнів пояснити, як вони розуміють цей рядок.)

ІІ. Актуалізація опорних знань

Вправа «Так чи ні?»

•   Чи правильно, що при переміщенні кожній точці фігури F відповідає єдина точка фігури F₁?  так
•   Чи правильно, що переміщення переводить відрізок у відрізок?  так
•   Чи правильно, що при русі не зберігаються кути між променями? ні
•   Чи правильно, що при  переміщенні будь-яка пряма переходить у пряму, що їй паралельна?  ні    
•   Чи правильно, що точка А₁ лежить між точками В₁ і С₁, якщо під час переміщення точки А, В і С переходять відповідно у точки А₁, В₁ і С₁ і точка С лежить між точками А і В? ні
•   Чи правильно, що дві фігури називаються рівними, якщо вони переводяться переміщенням одна в одну? так
•   Чи правильно, що два квадрати рівні, якщо їхні периметри рівні? так
•   Чи правильно, що два прямокутники рівні, якщо їх периметри рівні? ні
•   Чи існує переміщення, яке переводить відрізок із кінцями в точках А (0;1) і В (0;4) у відрізок із кінцями в точках М(1;3) і  К(1;5)? ні
•   Чи існує переміщення, яке переводить коло х²+у²=36 у коло х²+(у-2)²=36? так
•   Чи правильно, що довільний трикутник можна поділити на дві рівні частини? ні
•   Чи існує переміщення відносно точки? так

ІІІ. Мотивація навчальної діяльності

Симетрія оточує нас у повсякденному житті, вона спостерігається у будові тіла людини, тварин, рослин, молекул, симетричні будівлі ваблять око, симетричне розташування елементів побуту приносить гармонію у наше світосприйняття. ЇЇ використовують не тільки в геометрії, але й у фізиці, хімії, мистецтві , біології та архітектурі . Тому вивчення властивостей симетрії в просторі є важливим і актуальним.

В математиці розглядаються різні види симетрії: осьова симетрія (симетрія відносно прямої), центральна симетрія (симетрія відносно точки) і дзеркальна симетрія (симетрія відносно площини).

ІV. Вивчення нового матеріалу

Історичні відомості.

Симетрія — слово грецького походження і означає  співрозмірність, пропорційність, однаковість у розташуванні частин. Вперше поняття симетрії було введено у V ст. до н.е. філософом і геометром Піфагором. Він хотів підкреслити найважливішу сторону побудови світу — це його впорядкованість, організованість, симетрію, а значить і красу.

Видатний італійський вчений, дослідник, вихідник, художник, архітектор, інженер  Леонардо да Вінчі вважав, що пропорційність і гармонія, під якими він розумів симетрію, відіграють головну роль при створенні художнього твору.

Німецький художник, математик, теоретик мистецтва Альбрехт Дюрер стверджував, що правильні симетричні многогранники лежать в основі побудови креслень різних інженерних споруд, і тому кожен художник повинен знати способи побудови правильних симетричних фігур.

Німецький математик Герман Вейль у своїй книзі "Симетрія" проаналізував  перехід від простого чуттєвого сприйняття симетрії до її наукового розуміння. Згідно йому, під симетрією слід розуміти незмінність  будь-якого об'єкта за певного роду перетворень. Отже, можна сказати, що симетрія фігури  це будь-яке перетворення, що переводить фігуру в себе.

Сьогодні ми ознайомимося з перетворенням фігури за до­помогою симетрії відносно точки.

Практична робота №1

1. Позначимо довільні точки А і О.

2. Проведемо  промінь АО.

3. Відкладемо на ньому з другого боку від точки О відрізок ОВ (АО=ОВ).

Побудована таким чином точка В називається симетричною точці  А відносно точки О. 

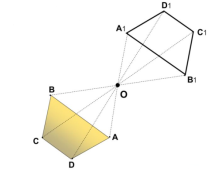
Точки  А і  В, називаються симетричними відносно точки О, якщо точки А, О, В лежать на одній прямій і точка О – середина відрізка АВ. Точка О називається центром симетрії.

Перетворення фігу­ри F на фігуру F₁, при якому кожна точка Х фігури F перехо­дить у точку Х₁ фігури F₁, симетричну точці X відносно даної точки О, називається перетворенням симетрії відносно точки О. Фігури F і F₁ називаються центрально-симетричними (симетрич­ними відносно точки О).

Властивості

1. Перетворення симетрії відносно точки є переміщенням.

2. Перетворення симетрії відносно точки перетворює пряму на паралельну їй пряму або на себе; відрізок – на рівний і паралельний йому відрізок; многокутник – на рівний йому многокутник.

3. Будь-яка пряма, що проходить через центр симетрії, відображається при цій симетрії на себе.

Запам’ятаємо

Якщо точка Х(х;у) симетрич­на точці Y(х₁; у₁) відносно початку координат О, то виконуються умови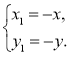

V. Засвоєння знань та формування навичок

Вправа 1 (Усно)

Серед точок А(5;3), B(-2;-4), C(-2;4), D(5;-3), K(-5;3), P(-5;-3), М(2;4) укажіть пари точок, які симетричні відносно початку координат.

Відповідь. А і Р; В і М.

Вправа 2 (Усно)

Точки А(3;-5) і С(1;1) симетричні. Знайти їх центр симетрії.

Відповідь. (2;-2).

Вправа 3 (Усно)

Складіть рівняння кола, симетричного колу з центром в точці О(2;-5) і радіусом 4см.

Відповідь.    і .

Вправа 4 (Усно)

Які з фігур мають центр симетрії? Де він розміщений?

Відповідь.  Відрізок, коло, паралелограм, рівносторонній трикутник.

Вправа 5

Побудувати відрізок А₁В₁ , симетричний відрізку АВ відносно точки О.

Вказівка. Будуємо промені АО і ВО та відкладаємо відрізки ОА₁=АО, ОВ₁=ВО.

Вправа 6

Побудувати кут А₁В₁С₁ , симетричний куту АВС відносно точки О.

Вказівка. Будуємо точки симетричні А, В, С відносно точки О.

Вправа 7

Побудувати трикутник, симетричний  трикутнику АВС відносно точки В.

Вказівка. Будуємо точки симетричні А, В, С відносно точки В.

Вправа 8

Побудувати точку, симетричну точці А(3;-4) відносно початку координат і точці В(2;5) відносно точки О(-1; 1).

Відповідь. А₁(-3;4) і В₁(-4;-3).

Вправа 9

Побудуйте чотирикутник А₁В₁С₁К₁ симетричний чотирикутнику АВСК, у якого А(2;3), В(4;1), С(2;0), К(-1;1), відносно початку координат.

Відповідь.  А₁(-2;-3), В₁(-4;-1), С₁(-2;0), К₁(1;-1).

Вправа 10

Записати рівняння прямої яка симетрична прямій 2х-5у=-7 відносно початку координат.

Відповідь.   2х-5у=7.

Вправа 11

Визначте кути ромба, якщо кут між діагоналлю ромба і перпендикуляром, що проведений з центра симетрії ромба до сторони, дорівнює 48°.

Відповідь.  84° і 96°.

Вправа 12

Кут між перпендикулярами  проведеними з центра симетрії до сторін ромба 60°. Знайти площу ромба , якщо сторона 6см.

Відповідь.   18см².

VІ. Підбиття підсумків

Запитання до класу

Про який вид переміщення ви довідались? (Симетрія відносно точки)

Яку фігуру дістаємо при симетрії відносно точки? (Рівну)

Які фігури називають симетричними?

Які фігури називаються центрально-симетричними?

Що мають квадрат, ромб, але не має рівносторонній трикутник? (Центр симетрії)

Як змінюються координати точки фігури при симетрії відносно початку координат? (На протилежні)

При послідовному виконанні двох симетрій відносно середини гіпотенузи, у яку фігуру перейде прямокутний трикутник? (У даний прямокутний трикутник)

VІІ. Домашнє завдання.

Складається з теоретичної частини – текст пункту підручника, та практичної – кількох вправ , подібних до завдань класної роботи та творчого завдання – знайти приклади симетричних фігур у навколишньому світі.