Урок "Симетрія відносно прямої".

 

Тема. Симетрія відносно прямої

Мета: сформувати поняття про симетрію відносно прямої, вчити будувати фігури симетричних даним відносно прямої; розвивати графічні здібності, логічне мислення; отримати уявлення про прояви симетрії в природі, різних галузях науки й людської діяльності;  застосовувати набуті вміння і знання для розв’язування різних задач на побудову і  обчислення.

Типи уроків: засвоєння нових знань, комбіновані.

Симетрія є тією ідеєю, за допомогою якої людина століттями намагається пояснити і створити порядок , красу і досконалість.

Герман Вейль

І. Організаційний момент

ІІ. Актуалізація опорних знань

«Мікрофон»

•      Яке означення симетрії відносно точки?
•      Чи можна стверджувати, що центральна симетрія є переміщенням?
•      Що таке центр симетрії фігури?
•      Скільки центрів симетрії має відрізок?
•      Яка фігура називається центральносиметричною?
•      Які властивості має центральна симетрія?
•      Яка точка є центром симетрії квадрата?
•      Який трикутник має центр симетрії?

ІІІ. Мотивація навчальної діяльності

«Мозковий штурм»

Чому симетрія пронизує весь навколишній світ?

•        Симетрією володіють об'єкти та явища живої природи.
•        Симетрію можна виявити майже скрізь, якщо знати, як її шукати.
•        Симетрія присутня в нашому житті буквально у всьому.
•        З симетрією ми зустрічаємося в мистецтві, техніці, побуті.
•        Симетрія є найважливішою складовою частиною будівлі.
•        Симетрія надає стійкості.
•        Симетрія встановлює внутрішні зв'язки між об'єктами і явищами.

Перетворення фігур (симетрія)  увійшло в математику в результаті спостереження людини за навколишнім світом. Природа - дивовижний творець і майстер. Все живе в природі має властивість симетрії.

Симетричні форми необхідні рибі, щоб плавати, а птиці, щоб літати. Властивість симетричності, властиве живій природі, людина використала у своїх досягненнях, винайшовши літак, машину, корабель.

 

 

 

 

ІV. Вивчення нового матеріалу

Сьогодні ми ознайомимося з перетворенням фігури за допомогою симетрії відносно прямої.

Притча про осьову симетрію

 Якось чужоземець, вражений красою Бухарського мінарету Кальян, вигукнув: “Як ви будуєте такі високі мінарети?” – “Дуже просто”, – відповів Ходжа Насреддін. І, хизуючись своєю дотепністю, пояснив: “Спочатку викопуємо глибокий колодязь, а потім вивертаємо його навиворіт”.

 

 

 

 

Практична робота №1

1. Позначимо довільну точку А і пряму k.

2. Проведемо перпендикуляр АО до прямої k.

3. Відкладемо на його продовженні від точки О відрізок ОВ (АО=ОВ).

 

 

 

 

 

 

 

 

 

 

Побудована таким чином точка В називається симетричною точці  А відносно прямої m.  Точки  А і  В, називаються симетричними відносно прямої k, якщо пряма АВ перпендикулярна прямій k і ОА=ОВ, де О – точка перетину прямих АВ і k.

Перетворення фігури F на фігуру F₁, при якому кожна точка Х фігури F переходить у точку Х₁ фігури F₁, симетричну їй відносно даної прямої k, називається перетворенням симетрії відносно прямої k або осьовою симетрією. Фігури F і F₁ називаються симетричними відносно прямої k, а пряма k – віссю симетрії.

 

 

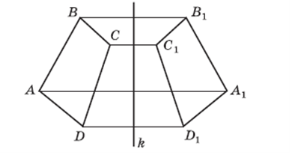
Властивості

1. Перетворення симетрії відносно прямої є переміщенням.

2. Перетворення симетрії відносно прямої перетворює пряму на пряму; відрізок –відрізок; многокутник – на рівний йому многокутник.

3. Точки, що належать осі симетрії, відображаються самі на себе.

Запам’ятаємо

Якщо точки Х(х;у) і Y(х₁; у₁) симетричні відносно:

1) осі Ох, то виконується умова 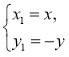  ;  2) осі Оу, то виконується умова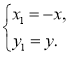

V. Засвоєння знань та формування навичок

Вправа 1 (Усно)

Кінці  відрізка знаходяться в точках А(-4;2) і В(3;1). Знайдіть координати кінців відрізка, симетричного заданому відносно: а) осі абсцис; б) осі ординат.

Відповідь.  а) (-4;-2) і (3;-1); б) (4;2) і (-3;1).

Вправа 2 (Усно)

Скільки осей симетрії мають геометричні фігури : ромб , паралелограм , коло , квадрат , правильний трикутник , рівнобедрений трикутник , рівнобічна трапеція .

Відповідь. ромб  – 2, паралелограм – 0, коло – безліч, квадрат – 4, правильний трикутник – 3, рівнобедрений трикутник – 1, рівнобічна трапеція – 1.

Вправа 3 (Усно)

Кінець середньої лінії рівнобічної трапеції віддалений від осі симетрії на 4 см. Знайдіть суму довжин основ трапеції.

Відповідь.16 см.

Вправа 4 (Усно)

Серед букв М, У, Е, Т, Ш, Щ, Х, С, А знайдіть зайві.

Відповідь.  Щ і У оскільки не мають осі симетрії.

Вправа 5 (Усно)

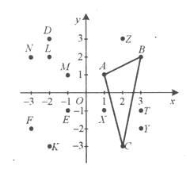
Визначте трикутник, симетричний трикутнику ABC відносно: а) осі абсцис; б) осі ординат;  в) початку координат.

Відповідь.  а) ∆ХYZ; б) ∆МNК;  в) ∆ЕFD.

 

 

 

 

 

Вправа 6

Побудуйте трикутник симетричний ΔABC, якщо A(2;-4), B(3;2), C(0; -2) відносно: а) осі Ох; б) осі Оу.

Відповідь. а)  A₁(2;4), B₁(3;-2), C₁(0; 2); б) A₂(-2;-4), B₂(-3;2), C₂(0; -2).

Вправа 7

Побудуйте трикутник симетричний ΔABC відносно прямої АС.

Вказівка. Побудуємо точку В₁ симетричну точці В відносно прямої АС.

Вправа 8

Побудуйте фігуру , симетричну даній прямокутній трапеції відносно прямої, яка містить її меншу діагональ.

Вказівка. Побудуємо точки симетричні кінцям більшої діагоналі відносно меншої діагоналі.

Вправа 9

Точка А ( 2 ; -3 ) і  В  симетричні  відносно прямої у = х . Знайдіть координати точки В.

Відповідь. (-2;3).

Вправа 10

Прямі 2х-у=0 і х+у=6 перетинаються в точці М. Знайти координати точки К симетричної точці М відносно осі абсцис.

Відповідь.   (2;-4).

Вправа 11

Точки перетину кола х²+у²=1 і прямої х-у=1 симетричні відносно якої прямої? 

Відповідь.   у = -х.

Вправа 12

Осями симетрії прямокутника є осі координат. Одна з вершин прямокутника має координати (-3;2). Знайдіть площу прямокутника.

 Відповідь. 24.

Вправа 13

Точка А симетрична точці В відносно точки О. Точка О лежить на 6 см від деякої прямої m , а точка А — на 2 см. На якій відстані лежить точка В від  прямої m , якщо А, О і В лежать в одній півплощині відносно даної прямої  і ОА не перпендикулярна до прямої m?

Відповідь.  10см.

Вправа 14

Діагоналі ромба належать на координатним осям. Знайдіть координати вершин ромба, якщо середина однієї з його сторін має координати (-2; 3).

Відповідь.  (-4;0), (0;6), (4;0), (0;-6) .

Вправа 15

Точка А(1;-2) симетрична точці А₁  відносно прямої у=х+3. Знайти координати точки А₁.

Відповідь.   (-5;4).

Вправа 16

 Вісь симетрії трапеції збігається з віссю Оу. Дві вершини її мають координати (-1; 1) і          (-3; -3). Назвіть координати двох інших вершин трапеції і координати кінців середньої лінії. Відповідь. (1;1), (3; -3), (-2;-1), (2;-1).

Вправа 17

Точки перетину осей симетрії прямокутника з його сторонами послідовно сполучено відрізками. Обчисліть периметр чотирикутника, який утворився, якщо довжина діагоналі даного прямокутника 20м.

Відповідь. 40м.

Вправа 18

Довести, що пряма проведена до основи рівнобедреного трикутника, яка містить висоту є його віссю симетрії.

Вказівка. Довести рівність трикутників.

VІ. Самостійна робота

Варіант 1

1. Знайдіть координати точок, симетричних точкам А(3;-2) і В(6;0) відносно: 1) осі абсцис; 2) осі ординат; 3) початку координат.

2. Побудувати фігуру, у яку перейде прямокутний трикутник АВС з прямим кутом В при симетрії відносно : 1) прямої. що містить висоту, проведену до гіпотенузи; 2) середини меншого катета.

3. Запишіть рівняння кола, у яке перейде коло+=25 при  симетрії відносно прямої у = х.

Варіант 2

1. Знайдіть координати точок, симетричних точкам А(-3;-4) і В(0;5) відносно: 1) осі абсцис; 2) осі ординат; 3) початку координат.

2. Побудувати фігуру, у яку перейде рівнобедрений трикутник АВС з тупим кутом В при симетрії відносно : 1) прямої. що містить висоту, проведену до бічної сторони; 2) середини бічної сторони.

3. Запишіть рівняння кола, у яке перейде коло+=49 при  симетрії відносно прямої у = -х.

Варіант 3

1. Знайдіть координати точок, симетричних точкам А(-4;5) і В(-3;0) відносно: 1) осі абсцис; 2) осі ординат; 3) початку координат.

2. Побудувати фігуру, у яку перейде різносторонній гострокутний  трикутник АВС при симетрії відносно : 1) прямої, що містить висоту, проведену до меншої сторони; 2) середини  більшої сторони.

3. Запишіть рівняння кола, у яке перейде коло+=36 при  симетрії відносно прямої у = х.

Варіант 4

1. Знайдіть координати точок, симетричних точкам А(5;-2) і В(0;-1) відносно: 1) осі абсцис; 2) осі ординат; 3) початку координат.

2. Побудувати фігуру, у яку перейде різносторонній гострокутний  трикутник АВС при симетрії відносно : 1) прямої, що містить медіану, проведену до більшої сторони; 2) середини  більшої висоти.

3.Запишіть рівняння кола, у яке перейде коло+=64 при  симетрії відносно прямої у = -х.

Відповідь.

І варіант.    1. 1) (3;2) і (6;0); 2)(-3;-2) і (-6;0); 3) (-3;2) і (-6;0);  3. +=25.

ІІ варіант.   1. 1) (-3;4) і (0;-5); 2)(3;-4) і (0;5); 3) (3;4) і (0;-5);   3. +=49.

ІІІ варіант.  1. 1) (-4;-5) і (-3;0); 2)(4;5) і (3;0); 3) (4;-5) і (3;0);  3. +=36.

ІV варіант. 1. 1) (5;2) і (0;1); 2)(-5;-2) і (0;-1); 3) (-5;2) і (0;1);   3. +=64.

 

       VІІ. Підбиття підсумків

VІІІ. Домашнє завдання.

Складається з теоретичної частини – текст пункту підручника, та практичної – кількох вправ , подібних до завдань класної роботи та творчого завдання – створити орнамент використовуючи симетрію.