Урок систематизації вмінь та навичок по темі: Застосування похідної та інтеграла при розв’язуванні задач

Урок систематизації вмінь та навичок по темі:

Застосування похідної та інтеграла при розв’язуванні задач

Необхідний час – 90хв.

  Мета уроку: - повторити означення похідної та інтеграла, їх властивості,

                                правила диференціювання та інтегрування;

- вчити учнів аналізувати та систематизувати ті знання, які

   вони отримують на уроках і черпають з додаткової             

   літератури;

- формувати наполегливість, увагу, зосередженість та

                                зацікавленість у результатах спільної роботи.

 Напис на дошці:  Розв’язання простої, але не зовсім стандартної задачі

                                    може вимагати деякого напруження, зате  натомість 

                                    дає відчути тріумф відкриття.

                                                                                                              за  Д.Пойа

      На уроці учні працюють групами, склад яких, заздалегідь продуманий вчителем, визначається на початку уроку. Кожній групі дається по кілька однакових задач (на розв’язання кожної з них відводиться 5-7хв.) з подальшою демонстрацією кожної задачі біля дошки. Біля дошки відповідає один представник групи, яка найшвидше справилася із завданням (на вибір капітана даної групи). Всі уважно слухають доповідача, після чого члени інших груп вносять свої пропозиції щодо розв’язання задачі, дають запитання доповідачеві. З’ясувавши шлях розв’язання задачі, учні записують його в зошити.

Структура уроку

1. Актуалізація опорних вмінь та навичок.
2. Узагальнення та повторення раніше здобутих знань.
3. Підсумок уроку.

Хід уроку

1. Повідомляється тема та мета уроку.
2. Актуалізація опорних вмінь та навичок (у формі фронтального опитування).

Питання для фронтального опитування:

1. Сформулювати означення похідної в точці.

2. Сформулювати правила диференціювання.

3. Дайте означення зростаючої та спадної функцій.

4. Сформулювати означення точок екстремуму та екстремумів функції.

5. Сформулювати означення первісної.

6. Скільки первісних можна знайти для одної функції?

7. Який інтеграл називають визначеним, а який невизначеним?

3. Узагальнення та повторення раніше здобутих знань.

    Оголошується склад груп. Кожна група отримує завдання та час на його виконання. Група, яка найшвидше справиться із завданням, починає його захищати біля дошки. Представники інших груп можуть вносити доповнення, спільно розв’язавши задачу всі записують її в робочий зошит.

• Для розминки групам пропонуються усні тренувальні вправи.
• Задачі, що будуть розглядатися на уроці:
• На початку другого уроку – тренувальні вправи на обчислення площ плоских фігур з допомогою інтегралів.

     1) Знайти загальний вид первісних для функції ;

     2) Розв’язати нерівність:

     3) Знайти площу фігури, обмеженої лінією , дотичною до неї                              

в точці з абсцисою і прямою .

     4) Знайти всі додатні числа , для кожного з яких

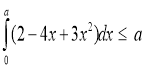
Д/з Знайти об’м тіла, одержаного при обертанні навколо осі OХ                                          криволінійної трапеції, обмеженої лініями .

4. Підсумок уроку.

     Ми узагальнили та повторили правила знаходження похідних та інтегралів. Розглянули нестандартні задачі. Як працювала кожна група? Які результати роботи?

5. Оцінювання.

Учні отримують оцінки, залежно від того, як працювали на уроці.