Урок "Сума n-перших членів геометричної прогресії"
Урок алгебри у 9 класі ( поглиблене вивчення)
Тема уроку: Сума n перших членів геометричної прогресії
Мета уроку: формування вмінь учнів обчислювати суму n перших членів геометричної прогресії та застосовувати відповідну формулу для розв’язання прикладних та нестандартних задач, розвиток самоосвітньої компетентності та цілеспрямованої розумової діяльності учнів шляхом застосування методики перевернутого навчання, виховання культури обчислювальних навичок
Тип уроку: формування вмінь та навичок
Обладнання: мультимедійний проектор, екран, персональні комп’ютери.
картки самоконтролю
Хід уроку:
І. Перевірка домашнього завдання
1.Самоперевірка практичних завдань
Відповіді: №5 1)18,6; 2)0 ;3) -117(![]() ; 4) 5; №6 -68,2
; 4) 5; №6 -68,2
2. Діагностична робота (тестове завдання з послідуючою перевіркою)
1) Обери правильно записану формулу n перших членів геометричної прогресії
|
А |
Б |
В |
Г |
|
|
|
|
|
2) Сума 17 + 172 + 173 + … + 1720 обчислюється за формулою:
|
А |
Б |
В |
Г |
|
|
|
|
|
3) Знайди суму n перших членів геометр. прогресії, якщо b1 = -4, q = -1, n = 9.
|
А |
Б |
В |
Г |
|
-4 |
4 |
2 |
0 |
4) Знайди суму п’яти перших членів геометричної прогресії ![]()
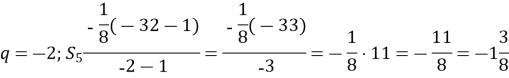
|
А |
Б |
В |
Г |
|
|
|
|
|
5) Склади математичну модель для розв’язання задачі «Купівля коня» (із «Арифметики» Магницького):
Продавець продав коня за 156 гр. Але покупець, придбавши коня, передумав і повернув господарю коня зі словами: «Кінь таких грошей не вартий». Тоді продавець запропонував такі умови: «Якщо ціна коня дуже висока, то купи лише цвяхи для його підків, а коня одержиш на додачу. Цвяхів у кожній підкові шість. За перший дай ![]() копійки, за другий
копійки, за другий ![]() копійки, за третій
копійки, за третій ![]() копійку і т.д. Покупець з радістю прийняв умови. Скільки повинен заплатити покупець і чи варто йому радіти?
копійку і т.д. Покупець з радістю прийняв умови. Скільки повинен заплатити покупець і чи варто йому радіти?
Розв’язання:
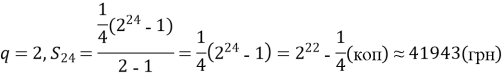
Індивідуальне завдання: довести справедливість формули ![]() , скориставшись формулою розкладу на множники двочлена an - bn.
, скориставшись формулою розкладу на множники двочлена an - bn.
ІІ. Актуалізація опорних знань (усний рахунок)
-
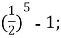 1)
1) 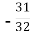 ;
;
-
 2)
2) 
-
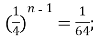 3) n=4;
3) n=4;
-
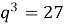 ; 4) q=3;
; 4) q=3;
-
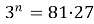 ; 5) n=7;
; 5) n=7;
-
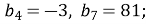 6) q= - 3;
6) q= - 3;
-
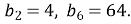 7) q= 2, q= -2.
7) q= 2, q= -2.
ІІІ. Формування вмінь та навичок
І група (Корекція знань)
1. Встановити відповідність між прогресіями та сумами 6 перших їх членів :
|
1. b1 = 4, b2 = 8 |
А. |
1 – Г |
|
2. b1 = -4, b2 = -2 |
Б. -252 |
2 – Д |
|
3. b1 = 12, b2 = -24 |
В. |
3 – Б |
|
4. |
Г. 252 |
4 – В |
|
|
Д. |
|
2. Знайди суму 6 перших членів геометр. прогресії (bn), якщо b1= - 4, b4= - ![]()
![]()
![]() ;
; 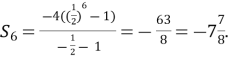
3. Знайти кількість членів геометр. прогресії (сn), якщо с1= - 9, q = - 2, Sn = - 99
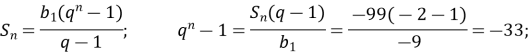
![]() n=5.
n=5.
4. Розв’яжи задачу
Бактерія, потрапляючи в сприятливе середовище, у кінці двадцятої хвилини ділиться на дві бактерії, кожна з яких у кінці наступних 20 хвилин ділиться знову на дві і т.д. Скільки бактерій утворюється з однієї протягом робочого дня (8год)?
Розв’язання:
![]()
![]()
ІІ група (завдання достатнього рівня виконує за комп’ютерами)
-
Знайди
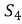 , якщо b4 = 10, b7 = 10000.
, якщо b4 = 10, b7 = 10000.
Розв’язання: ![]()
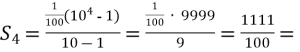 11,11
11,11
а) 11,1; б) 1,11; в) 11,11; г) 111,1.
2. Знайди кількість членів геометр. прогресії, якщо ![]() , b1 = 8,
, b1 = 8, ![]()
Розв’язання:
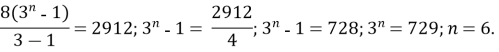
а) 4; б) 8; в) 5; г) 6.
3. Дано: ![]()
![]() . Знайти перший член прогресії.
. Знайти перший член прогресії.
Розв’язання: 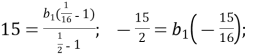
![]()
а) ![]() ; б) 8; в) -8; г)
; б) 8; в) -8; г)![]() .
.
Завдання високого рівня (індивідуальні завдання)
№36.18
Доведіть, що ![]()
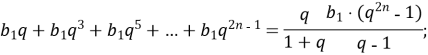
![]() , що й треба було довести.
, що й треба було довести.
№36.19 (збірник завдань Сканаві. №4.051)
Знайти суму![]()
Розв’язання:
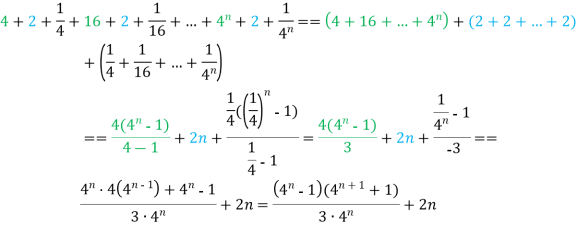
ІV. Підсумки уроку (аналіз карток самоконтролю, дебрифінг)
V. Домашнє завдання
Cамостійно ознайомитися з темою “Сума нескінченної геометричної прогресії за допомогою п.37 підручника, відеоролика за адресою math-nit blogspot.com


про публікацію авторської розробки
Додати розробку
