Урок з геометрії "Розв’язування задач з теми "Трапеція""

Про матеріал

Конспект уроку з геометрії для 8 класу "Разв’язання задач з теми "Трапеція""

Перегляд файлу

Тема: Розв’язання задач з теми «Трапеція».

Мета:

Узагальнити та систематизувати теоретичні знання учнів з теми; закріпити уміння та навички при розв’язанні задач, удосконалювати уміння учнів розв’язувати задачі про трапеції та на застосування теореми про середню лінію трапеції.
Розвивати кмітливість, логічне мислення.
Виховувати здатність учнів до самостійних дій та до самостійного творчого мислення.

Обладнання: проектор, ПК або ноутбук, зображення на екрані моделей різних видів трапецій (рівнобічних, прямокутних, довільних); малюнки до задач; схема переміщення; картки з текстами задач для класної та для домашньої робіт.

Хід уроку:

І. Організаційний момент.

ІІ. Перевірка теоретичного матеріалу.

Робота в групах.

3 – 4 групи (по 4 – 5 учнів).

Від кожної групи один учень отримує завдання на вибір № 2, № 3, № 4, № 5. Поки учні виконують ці завдання, на дошці заповнюється таблиця (завдання № 1), для цього від кожної групи по черзі виходить учень і записує необхідні позначення в будь яку строку таблиці (інші роблять подібні записи в зошиті).

Заслуховуються відповіді учнів, які виконували індивідуальні завдання (№ 2, № 3, № 4, № 5). Завдання № 6 використовується, як додаткове питання у випадку неправильної відповіді.

№ 1 Розгляньте малюнок. Позначте на ньому трапецію ABCD і заповніть таблицю:

ABCD – трапеція	Позначення	Особливості
Вершини: а) сусідні б) протилежні
Сторони: а) сусідні б) протилежні
Кути: а) сусідні б) протилежні
Діагоналі

№ 2 Проаналізуйте означення трапеції та викресліть некоректне:

Трапеція – це паралелограм тільки з двома паралельними сторонами;
Трапеція – це чотирикутник з двома паралельними сторонами;
Трапеція – це чотирикутник у якого тільки дві сторони паралельні.

№ 3 Розподіліть зображені на малюнках трапеції так, щоб до першої групи ввійшли рівнобічні трапеції, до другої групи – прямокутні, а до третьої – довільні трапеції :

№ 4 На якому малюнку зображена трапеція зі своєю середньою лінією? (Дати означення середньої лінії трапеції).

№ 5 Чому дорівнює середня лінія трапеції:

Сумі основ трапеції;
Полусумі основ трапеції;
Добутку основи на висоту;
Свій варіант означення.

№ 6 Периметр трапеції:

Добуток чотирьох сторін трапеції;
Сума всіх чотирьох сторін трапеції;
Свій варіант.

ІІІ. Розв’язання задач.

«Пошук дороги до храму» - переміщуватися за картою, виконуючи завдання.

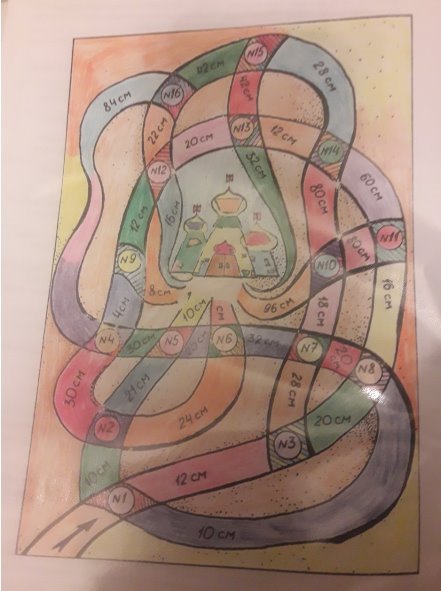
$C:\Documents and Settings\Admin\Local Settings\Temporary Internet Files\Content.Word\20200221_230401.jpg$

Шістнадцять перехресть на шляху до храму Трапеції – шістнадцять задач, більшу частину яких треба розв’язати, щоб відшукати істину дорогу, яка веде до відчиненого входу до храму. Номер перехрестя відповідає номеру задачі, а відповідь до неї вказує подальший напрямок руху.

Перехрестя	Умова задачі
№ 1	Три сторони трапеції дорівнюють по 2 см, кути при більшій основі по 60⁰. Знайдіть периметр трапеції.
№ 2	Діагоналі трапеції ділять її середню лінію на частини, кожна із яких дорівнює 6 см. Знайти нижню основу трапеції.
№ 3	В прямокутній трапеції гострий кут дорівнює 60⁰, більша бічна сторона дорівнює 32 см, менша основа – 12 см. Знайти довжину середньої лінії.
№ 4	Основи трапеції дорівнюють 60 см та 20 см. Знайти довжину відрізка, який з’єднує середини діагоналей цієї трапеції.
№ 5	Бісектриси гострих кутів при нижній основі трапеції перетинаються на її верхній основі. Знайти довжину верхньої основи, якщо бічні сторони дорівнюють 6 см та 4 см.
№ 6	В прямокутній трапеції гострий кут дорівнює 45⁰, менша бічна сторона дорівнює 8 см, а середня лінія 28 см. Знайти довжину верхньої основи.
№ 7	Середня лінія і кожна із бічних сторін трапеції дорівнюють по 12 см, кут біля меншої основи 120⁰. Знайти довжину більшої основи.
№ 8	Кут при основі рівнобічної трапеції 60⁰. Бічна сторона дорівнює 4 см та перпендикулярна одній з діагоналей. Знайти периметр трапеції.
№ 9	В трапеції *ABCD* основа AD і BC дорівнюють відповідно 20 см та 8 см, а бічні сторони 11 см та 9 см. Бісектриси кутів A і B перетинаються у точці P, а бісектриси кутів C і D – в точці Q. Знайти довжину відрізка PQ.
№ 10	Середня лінія трапеції 24 см. Знайти її периметр, якщо відомо що трапецію можна розрізати на ромб та рівносторонній трикутник.
№ 11	Знайти периметр рівнобічної трапеції, якщо її гострий кут 60⁰, а основи 30 см та 10 см.
№ 12	Прямокутна трапеція ділиться діагоналлю на два трикутника - рівносторонній із стороною 16 см та прямокутний. Знайти середню лінію трапеції.
№ 13	В трапеції *ABCD* менша основа BC дорівнює відповідно 4 см. Через вершину В проведена пряма паралельна бічній стороні. Периметр трикутника що утворився дорівнює 12 см. Знайти периметр трапеції.
№ 14	Периметр трапеції 72 см, кути при більшій основі по 60⁰. Діагональ ділить середню лінію на частини, одна із яких на 8 см більше за іншу. Знайти більшу основу трапеції.
№ 15	В рівнобічній трапеції діагональ ділить гострий кут навпіл. Периметр трапеції дорівнює 132 см, основи відносяться як 2:5. Знайти середню лінію трапеції.
№ 16	Діагональ трапеції ділить середню лінію на відрізки, довжина яких співвідносяться як 11:21. Знайти більшу основу трапеції, якщо різниця довжин цих відрізків дорівнює 20 см.

Умови виконання та правила:

Низький рівень – виконати креслення, визначитись які формули слід використовувати для розв’язання задачі.

Середній та достатній рівні – виконати креслення та розв’язати задачу.

Учні виконують завдання, вчитель перевіряє та оцінює.

Можна використати «ПОМІЧНИКА» (1 раз – 0,5 бала)

IV. Підсумок.

Протягом уроку заповнюється таблиця результатів:

№	ПІ учня	Номер завдання та кількість балів за його виконання
№	ПІ учня	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22

Підраховуються бали та оцінюється робота учня.

V. Кожен учень отримує завдання, аналогічне тому, де були припущені помилки. Аналізуючи виправлення вчителя, учень повинен розв’язати задачу та записати теоретичну основу (яка необхідна для розв’язку).

docx

Завантажити

Зберегти на потім

Додав(-ла)

Дерев’янко Наталія Анатоліївна

Пов’язані теми

Геометрія, 8 клас, Розробки уроків

Додано

22 лютого 2020

Переглядів

7627

Оцінка розробки

Відгуки відсутні