урок теоретичного навчання
Державний навчальний заклад «Лісоводський професійний аграрний ліцей»
Конспект уроку з математики на тему: : «Площа поверхні призми»
Розробила: викладачка математики Повх Л.М.
Учень 1.
Світає…Тільки-що но стало на світ благословлятись. А орач у полі. Його трактор, мов могутній велетень, під силу якому все, впевнено заїхав на ниву.
Роздивився навкруги – куди не кинь оком, аж до небокраю – земля,на якій залишилося стерня не так давно зібраного збіжжя. Земелько моя, земелько! Як мило на тобі працювати, як серцю любо бачити пшеничний лан, що перешіптується із світанками та переспівується із жайвороном. Жнива минули. І на часі робота його, орача.
Загула машина, і вправні хліборобські руки вміло повели кермо по полю.
Скиба за скибою, рівно лягали за плугом. Масний чорнозем вимальовувся узором на жовтому від стерні полі. Орач впевнено долав метр за метром, і за ним з’являлося більше зораного поля. Оглянувся – сходило сонце, а земля вилискувала барвами, виспівувала голосами поля, усміхалася трударю.
Цілий день орач невтомно працював – орав. А до вечора, коли стало сідати за горизонт сонце, усміхнено, задоволений результатом своєї праці, зітхнув.
Цим орачем, що понад 20 літ обробляє землю, був мій батько. Можливо, завдяки батькові, у мене з дитинства була заповітна мрія – стати хліборобом, працювати на землі. Сьогодні вона майже здійснилася. Я учень ДНЗ «Лісоводський ПАЛ», навчаюсь за професією «Слюсар з ремонту сільськогосподарської техніки; тракторист-машиніст сільськогосподарського (лісогосподарського) виробництва категорій «А1, А2. Водій автотранспортних засобів категорії «С».
У майбутньому мені обробляти поле і вирощувати врожаї, щоб Україна була багатою та ситою. Окрім того, що Лісоводський аграрний ліцей навчає мене спеціальності, я ще навчаюсь господарювати за школою великого хлібороба, геніального менеджера, який опередив свій час – Григорія Івановича Ткачука.
Учень 2.
Лісоводи і Ткачук Г.І. – це тема окремої розмови. Ще із сорокових років минулого століття, коли сільське господарство очолив відомий на Поділлі голова колгоспу Григорій Іванович Ткачук, різного роду підрахунки були рушійною силою збагачення колгоспу. «Хто копійчину не рахує за гроші, - той і сам нічого не вартий» - говорив Григорій Іванович і навчив селян вкладати гроші, прогнозувати прибуток.
Григорій Іванович Ткачук був великим господарем на землі, тому у ДНЗ «Лісоводський ПАЛ» існує традиція навчитись працювати за Г.І. Ткачуком: вміти рахувати, берегти майно, любити свою роботу, трудитись з повною віддачею.
На сьогоднішній день дуже важливо вміти грамотно рахувати у будь-який галузі сільського господарства, промисловості, економіки, щоб не залишитись у програші. Цієї науки навчав також Григорій Іванович Ткачук, цієї науки навчаємо Вас, учні, викладачі і майстри виробничого навчання.
Ви можете вкотре мене запитати: «Для чого механізатору математика? Аби добре знав техніку та вмів нею керувати».
Це не так. Механізатор повинен досконало знати трактор, вміти працювати на землі, але ще й мати вагомий багаж знань математики, інформатики, без компетентностей грамотності Ви не зможете йти в ногу з часом, так як сучасна техніка оснащена комп’ютерами.
У час,коли країна переходить великою мірою до приватної форми власності особливо важливо вміти здійснювати підрахунки, щоб мати гарні заробітки.
Якщо Ви, учні, будете працювати у приватній фірмі, наприклад, «Вітагро» і «Мрія Континентал», яка має багато землі, то всі обрахунки виконують спеціалісти. Але там новітня техніка і потрібно добре знати комп’ютер.
Більшість з Вас проживає у селі, селяни мають присадибні ділянки, соціальні сфери, земельні паї. Можливо у Вас є своя техніка, а хтось із Вас придбає. Вас попросять зорати, закультивувати, посіяти. І тут Вам потрібно вміти розрахувати норми висіву насіння, глибину оранки та культивації, витрати паливно-мастильних матеріалів ,площі зораних і засіяних полів, кількість зібраних центнерів зернових, підрахувати прибуток.
Учні, дай Боже, щоб хтось із Вас став орендарем, то тоді математика буде дуже Вам потрібна. Всі розрахунки і підрахунки ляжуть на Ваші плечі. Бо яка б не була нова техніка, а людина завжди потрібна.
Тема: «Площа поверхні призми».
Мета: 1. Навчити обчислювати площу бічної і повної поверхні призми;
2. Розвивати творчу уяву про призму;
3. Виховувати математичну грамотність, інфляційно-цифрову компетентність, вміння спілкуватись державною мовою.
Тип уроку: комбінований.
Методи і прийоми: монолог учня «Орач…», мультимедійна презентація «Математика у моїй професії», пояснення викладача, розв’язування задач.
Обладнання: мультимедійні засоби навчання, підручники, математичні фігури.
Хід уроку
І. Актуалізація опорних знань і мотивація.
1. Монолог учня.
2. Демонстрація слайдів.
3. Слово викладача.
ІІ. Повторення вивченого матеріалу.
На попередньому уроці ми приступили до вивчення розділу «Многогранники» і зокрема ознайомились з одним із них – призмою, її елементами і видами. Повторимо.
Слайд 1 Бачимо многогранник, кулю, конус, циліндр.
- Як називають ці фігури? (Геометричними тілами, або тілами.)
- Яке тіло називається многогранником? (Поверхня якого складається з скінченої кількості многокутників).
- Які грані називаються сусідніми? (Які мають спільне ребро).
Сллайд 2
- Многогранник, дві грані якого – рівні n-кутники, що лежать у паралельних площинах, а решта n граней – паралелограм, називається? (n-кутною призмою);
- Паралелограми – (бічні грані призми);
- n-кутники – (основи призми);
- сторони основ – (ребрами основ призми);
- ребра, які не належать основам – (бічними ребрами призми);
- перпендикуляр, опущений з якої-небудь точки площини однієї основи на площину другої основи називається (висотою призми).
Слайд 3
- Призму називають прямою, якщо (її бічні ребра перпендикулярні до площини основи).
- Якщо призма не є прямою, то її називають (похилою).
- Пряму призми називають правильною, якщо (основою є правильний многокутник).
Слайд 4
- Переріз призми площиною, яка проходить через бічне ребро призми і діагональ основи називається (діагональним перерізом призми).
- Діагональним перерізом прямої призми є (прямокутник).
- Наведіть приклади призми, які бачите навколо себе.
Вивчення нового матеріалу
Оз1. Площею бічної поверхні призми називають суму площ усіх її бічних граней.
О2. Площею поверхні призми називають суму площ усіх її граней. (говорять що «площа повної поверхні призми»).
Отже, виконується рівність Sn=Sб+2Sосн.,
де Sn – площа поверхні призми, Sб – площа бічної поверхні призми,
Sосн. – площа основи призми.
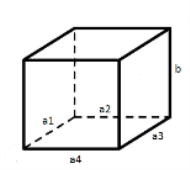 Т.16.1. Площа бічної поверхні прямої призми дорівнює добутку периметра її основи та бічного ребра призми.
Т.16.1. Площа бічної поверхні прямої призми дорівнює добутку периметра її основи та бічного ребра призми.
Доведення
Кожна бічна грань прямої призми – прямокутник, одна сторона якого – ребро основи, а друга – бічне ребро. Нехай а1, а2 , …, аn – довжина ребер основи призми,
b – довжина бічного ребра. Тоді Sб = a1b+a2b+ … + anb = b (a1+a2 + … + an).
Сума в дужках дорівнює периметру основи призми, то теорема доведена.
Отже, S б = Росн. * b, де Росн. – периметр основи призми, b – довжина бічного ребра.
IV. Закріплення вивченого матеріалу
Слайд 5
Задача 1. На малюнку зображено правильну чотирикутну призму, сторона основи якої дорівнює
2 см, а бічне ребро – 5 см. Знайдіть:
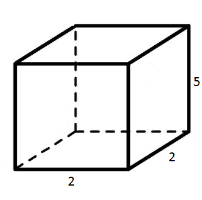 А) площу бічної грані (2*5=10 см2)
А) площу бічної грані (2*5=10 см2)
Б) Площу основи (4 см2)
В) Площу бічної поверхні (Sб = 8*5 = 40 см2)
Г) Площу поверхні призми (Sб + 2Sосн. = 40+2*4 = 40+8=48 см2)
Ґ) Діагональ основи 2![]() (см)
(см)
Д) Діагональ бічної грані (![]() =
= ![]() см).
см).
Задача 2. Основою прямої призми є рівнобічна трапеція, один із кутів якої дорівнюєм 110°. Знайдіть двогранні кути. Знайдіть площу повної поверхні правильної трикутної призми, сторона основи якої дорівнює а, а висота – Н.
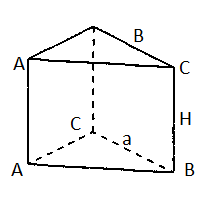 Sn=Sб+2Sосн.
Sn=Sб+2Sосн.
Sб = Росн. * Н = 3а * Н
Sосн. = ![]() а2
а2
Sосн. = 3аН + 2 ![]() а2 = 3аН +
а2 = 3аН + ![]() а2
а2
Задача 3. Знайдіть сторону основи правильної семикутної призми, висота
якої дорівнює
10 см, а площа бічної поверхні – 420 см2.
Розв’язок.
Нехай ребро основи призми – х. Тоді
Sбіч. = 7х*10 = 420
х = ![]() = 6 (см).
= 6 (см).
Задача 4. Знайдіть площу діагонального перерізу правильної чотирикутної призми, висота якої дорівнює 10 см, площа основи – 144 см2.
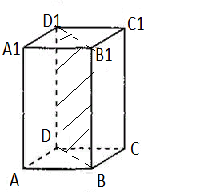 Дано: Sосн. = 144 см2
Дано: Sосн. = 144 см2
АА1 = 10 см
Sпер - ?
Sосн. = х2 = 144
Х = 12 (см)
З ∆ ABD BD = ![]() 122+122 =
122+122 = ![]() = 12
= 12![]() (см).
(см).
Тоді Sпер. = 12![]() * 10 = 120
* 10 = 120![]() (см2).
(см2).
Задача 5. Площа поверхні правильної чотирикутної призми – 40 см2, а бічної поверхні – 32 см2. Знайдіть висоту призми.
Дано: Sпов. = 40 см2
Sбіч. = 32 см2
Н-?
2Sосн. = 40 – 32 = 8 см2
Sосн. = 4м см2
АВ = 2 см
4*2*Н=32
Н = 8 см
Підсумки уроку
V. Домашнє завдання.
§ 4 п.16, № 6.20.


про публікацію авторської розробки
Додати розробку
