Урок "У пошуках скарбів"

У ПОШУКАХ СКАРБІВ

 

 

Тема: Декартові координати на площині.

          Координати середини відрізка. Відстань між точками.

 

 

Дидактична мета: вчити учнів знаходити положення точки на площині,  

    визначати координати середини відрізка; знаходити

    відстань між точками;

    вчитися описувати геометричні фігури алгебраїчними

    виразами.

Розвиваюча мета: розвивати просторову уяву; навики креслення; логіку

    мислення; навики самоконтролю і взаємоконтролю.

Виховна мета:      виховувати культуру праці (акуратність, увагу, культуру

    письма і усної мови); наполегливість у праці;

    почуття колективізму.

Засоби навчання: підручник «Геометрія 9кл.»; мультимедійна презентація; класна дошка; креслярські інструменти; комплекти наочностей;  комп'ютер, мультимедійний проєктор.

 

Структура уроку

 

1. Організація класу.

2. Актуалізація опорних знань учнів.

3. Вивчення нового матеріалу.

4. Вправи на закріплення нового матеріалу.

5. Підведення підсумків.

6. Домашнє завдання.

 

Зміст уроку

 

 - Добрий день!

 Сьогодні ми розпочинаємо вивчати нову тему: «Декартові координати на площині». Знання, які ви отримаєте під час наших уроків допоможуть вам побачити зв'язок, що існує між найважливішими геометричними фігурами і алгебраїчними рівняннями.

 Починаємо ми вивчати тему з найпростішого – визначення положення точки на площині, знаходження середини відрізка і відстані між точками.

 Частково ви вже знайомі з цією темою з курсу 6-го класу, а значить нам буде легше опановувати новий матеріал.

 

 Ви об'єдналися у групи, які умовно мають назви: «Теоретики», «Логіки», «Піфагорійці», «Фізкультурники», «Діогени». Кожна група отримала своє завдання, яке повинна була виконати самостійно. І тепер ви маєте можливість поділитися своїми знаннями. Весь урок нам буде допомагати комп'ютер.

 Все повинно мати свою назву. Я назвала наш урок «У пошуках скарбів, або Декартові координати на площині». А що це за скарби, і чи знайшли ми їх – відповідь на це ви дасте мені в кінці уроку.

 

 - В деякому царстві, в деякому государстві жив цар. Дуже злий він був. Придумував різні завдання люду, а якщо хтось не виконував – голову рубав.

 Одного разу викликав він свого служника і наказав йому піти туди – незнамо куди, і знайте – незнамо що. А Іван каже царю: «Піду, якщо координати вкажете». Довго думав цар, що таке координати, але так і не знайшов відповіді. Пошукаємо її разом.

 

 - Слово надається групі «Теоретики».

Основні питання.

• Необхідність введення координат.
• Відтворення відомих знань про прямокутну систему координат.
  • Осі координат.
  • Початок координат.
  • Координати точки.
  • Знаки координат.

 

 

Завдання №1.

Побудувати на координатній площині точки А(3; -2), В(-2; 2), С(2; 4). Попарно сполучити ці точки відрізками. Яка фігура утворилась?

 

 

 

 

 

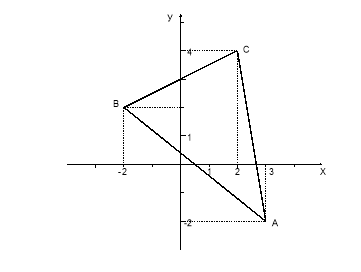
 - Тепер всі разом виконаємо наступне завдання. Увага на екран.

 

 Завдання №2.

 Побудувати на координатній площині точки А(1; 4), В(4; 1), С(1; -2), Д(-2; 1). Попарно сполучіть ці точки і назвіть фігуру, яку отримали.

• Як називаються відрізки АС, ВД?
• Що позначає точка К?

 

 

 

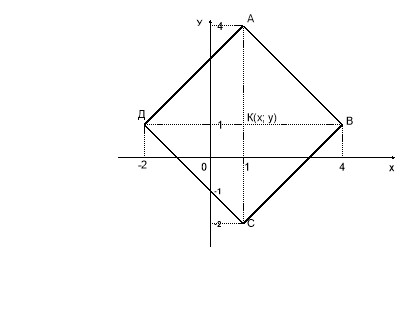
 - А як знайти середину відрізка? Про це нам розкаже група «Логіків».

Основні питання.

• Вивідення формули для визначення координат середини відрізка.

 

- Повертаємось до нашого малюнка. Яким чином ще можна дізнатися координати точки К. (Довжину відрізка поділити на два).

- А що таке довжина відрізка? Як її знайти? З'ясуємо трошки пізніше.

 А тепер трошки відпочинемо. Слово надається групі «Фізкультурники», яка повинна була підготувати фізкультхвилинку з використанням елементів геометрії, а саме – знать про різні види кутів.

Основні питання.

• Гострий кут.
• Прямий кут.
• Тупий кут.
• Розгорнутий кут.

 

- Всі трохи відпочили і тепер виконаємо самостійне завдання.

 

 

 

Самостійна робота

 

В -1                                                                В – 2

Визначити координати середини відрізка

АВ, якщо А(-4; 1), В(2; 3).                        СД, якщо С(3; 1), Д(3; -3).

К(х; у) - ?             Е(х;у) - ?

 Виконати відповідний малюнок.

 

    - Перевіряємо. Взаємоконтроль.

 

х = (х₁ + х₂)/2

у = (у₁ + у₂)/2

х = (-4 +2)/2=-2 : 2 = -1                                х = (3 + 3)/2 = 6 : 2 = 3

у = (1 + 3)/2 = 4 : 2 = 2                                 у = (1 + (-3))/2 = -2 : 2 = -1

К(-1; 2)                                                          Е(3; -1)

 

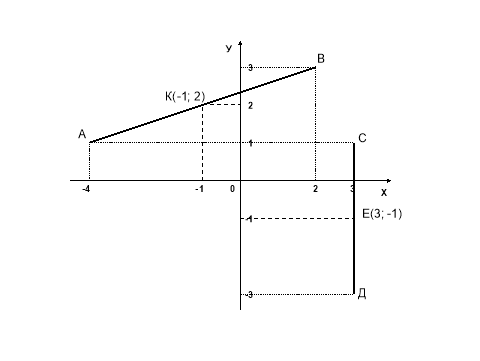                                            - В кого правильно виконане завдання – поставили 4 бали.

Коли відрізок паралельний вісі координат – його довжину знайти дуже просто. А якщо ні? Як тут бути? Відповідь на це питання нам дасть група «Піфагорейці».

Основні питання.

• Вивести формулу для визначення відстані між точками.
• Довести, що формула вірна і для випадків, коли х₁ = х₂, чи у₁ = у₂.

 

    - Тепер всі разом виконуєм завдання №3.

 

 

 

Визначити відстань між точками А(1; 0,5), В(5; 3,5). (Усно). Увага, на екран.

 

 

          

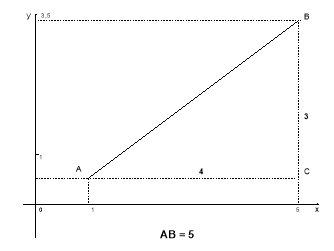
 Самостійна робота

 

Визначити відстань між точками А(-2; 6), В(4; -2).

 

 

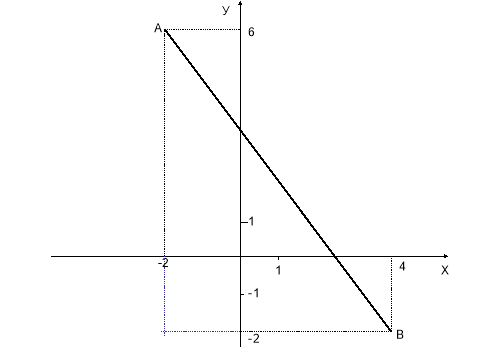
Під час виконання самостійної роботи можна попросити допомоги у товариша.

    Перевіряємо. Самоконтроль. (За правильно виконане завдання – 2 бали; виконане з допомогою – 1бал).

           _________________      _______      ___

АВ = √(-2 – 4)² + (6 – (-2))²= √(-6)² + 8² =√100 = 10

 

    - Ми навчилися позначати точки на координатній площині, визначати відстань між ними і визначати координати середини відрізка. Але виникає питання: «Яке практичне значення має цей матеріал?» Відповідь на це питання нам дає група «Діогени».

Основні питання.

• Практичне застосування матеріалу урока.

 

• Будівельна справа.
• Визначення відстані між кораблями.

 

    - Повертаємось до початку уроку. Чи можемо ми сказати, що ми опанували всі питання нашої теми? А чи знайшли скарби? Які вони?

 

     Виставлення оцінок.

Домашнє завдання. §3,  № 72, 78,80.