Урок-узагальнення по темі: "Арифметична та геометрична прогресії"
Тема уроку: Узагальнення по темі „Послідовності”.
Мета уроку: узагальнити і систематизувати знання учнів з даної теми, сприяти формуванню стійкого пізнавального інтересу до математики, розширювати кругозір учнів, здійснювати міжпредметні та міжкурсові зв’язки.
Обладнання: етимологічний словник, портрети Фібоначчі, Ферма, Вієта, аль-Біруні, ілюстрації.
Тип уроку: урок систематизації і узагальнення.
Форма проведення: урок- захист творчих завдань.
Епіграф уроку: Математика безмежно різноманітна, як світ, і присутня , міститься в усьому ( Єругін).
Хід уроку
І. Організаційний момент
ІІ. Повідомлення теми та мети уроку
Ми завершили невелику за обсягом, але не за значенням тему. Тема, яку ми вивчали була прогресом, кроком вперед у наших знаннях з математики. А на сьогоднішньому уроці ми покажемо широке застосування її в науці, природознавстві, техніці, при розв’язуванні складних математичних завдань.
Урок ми проведемо в формі захисту творчих завдань. Ваші виступи будуть оцінювати представники, члени шкільного наукового товариства районного відділення МАН. Оцінюватимуться ваші виступи за певними критеріями: науковість, повнота, доступність, вміння спілкуватись, вести наукову дискусію. Крім цього ви можете принести собі додаткові бали, поставивши запитання своїм опонентам. Ваші бали члени журі заноситимуть до таблиці
|
Прізвище, ім’я |
Якість доповіді:композиція, повнота подання роботи аргументованість, обсяг тезауруса, переконливістьі переконаність |
Обсяг і повнота знань з теми |
Культура мовлення, використання наочних посібників, почуття часу, утримання уваги аудиторії |
Поставлені питання опонентам |
Ділові і вольові якості доповідача: відповідальне ставлення до досягнення високих результатів, готовність до дискусії, контактність |
Відповіді на запитання; повнота , аргументованість, дружелюбність |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ІІ. Актуалізація опорних знань учнів.
Дати означення числової послідовності, арифметичної та геометричної прогресії, рекурентного способу задання послідовності.
Етимологічний словник з теми.
1. Рекурентний – від латинського слова recurro – повертаюсь.
2. Прогресія. Слова „прогресія”, „прогресивний”, „прогрес” – одного кореня. Прогресія – це послідовність, побудована за таким правилом, який дає їй змогу продовжувати необмежено, тобто рухатись вперед.
Термін „прогресія” вперше зустрічається у римського вченого Боеція (V-VІ ст.) У ХVІІ ст. поряд з терміном „прогресія” почали використовувати для позначення послідовності термін „ряд”.
Про арифметичну та геометричну прогресії складено багато цікавих задач, до нас дійшло багато легенд. Група учнів підготувала інсценізацію легенди про винахід шахів.
Виступ учнів першої групи.
Ведучий.
Шахи – одна з найдавніших ігор. Вона існує багато віків, і не дивно, що з нею пов’язані різні перекази, правдивість яких через давність часу неможливо перевірити.
З однією з них ми сьогодні й ознайомимось. Щоб зрозуміти її, зовсім не треба вміти грати в шахи: досить знати, що гра відбувається на дошці, поділеній на 64 клітинки (чорні та білі).
Шахову гру було придумано в Індії, і коли індуський цар Шерам був ознайомлений з нею. Він був у захопленні від неї.
Довідавшись, що її винайшов один із його підданих, він наказав покликати його, щоб особисто нагородити за вдалу видумку.
Винахідник, його звали Сета, з’явився перед троном повелителя. Це був скромно одягнений учений, що заробляв на життя, навчаючи інших.
Цар Шерам. Я бажаю гідно нагородити тебе, Сето, за чудову гру, яку ти придумав.(Мудрець вклоняється)
Цар. Я досить багатий, щоб виконати найсміливіше твоє бажання. Назви нагороду, яка тебе задовольнить, і ти одержиш її.
(Сета мовчить)
Цар. Не бійся, вислови своє бажання. Я не пошкодую нічого, щоб виконати його.
Сета. Велика добрість твоя, повелителю. Але дай строк обміркувати відповідь. Завтра я повідомлю тобі моє прохання.
Ведучий. На другий день Сета знову з’явився в палаці.
Сета. Повелителю, накажи видати мені за першу клітинку шахівниці одне зерно.
Цар .(здивовано) Просте пшеничне зерно?
Сета. Так, повелителю. За другу клітинку – накажи видати мені два зерна, за третю – чотири, за четверту – вісім, за п’яту – шістнадцять...
Цар (роздратовано). Досить. Ти одержиш свої зерна за всі 64 клітинки дошки, як бажаєш: за кожну наступну вдвічі більше, ніж за попередню. Але знай, що прохання твоє недостойне моєї щедрості. Просячи таку мізерну нагороду, ти нехтуєш моєю милістю. Воістину, як учитель ти міг би показати кращий приклад поваги до милості і щедрості свого повелителя. Іди. Слуги мої винесуть тобі твій мішок з пшеницею. (Сета посміхнувся і покинув замок).
Ведучий. Після обіду цар згадав про винахідника шахів і надіслав слугу дізнатися, чи виніс нерозсудливий Сета свою мізерну нагороду.
Цар. Чи отримав Сета свій мішок з зерном?
Слуга. Повелителю! Наказ твій виконується. Придворні математики підраховують кількість належних зерен. (Слуга виходить)
Ведучий. Цар нахмурився, він не звик, щоб його повеління виконувалось так довго. Увечері, ідучи спати, цар ще раз звернувся до придворних.
Слуга. Повелителю! Математики твої невтомно працюють і сподіваються ще до світанку закінчити роботу.
Цар. Чому зволікають з цією справою? Завтра, до того, коли я прокинуся, все до останньої зернини повинно бути віддано Сеті. Я двічі не наказую!
Ведучий. Вранці цареві доповіли, що старшина придворних математиків просить вислухати важливе повідомлення. Цар наказав йому зайти.
Цар. Перед тим, як ти казатимеш про інші справи, я бажаю почути, чи видано, нарешті, Сеті ту мізерну нагороду, яку він сам собі призначив.
Старшина придворних математиків. Заради цього я і насмілився з’явитися до тебе в таку ранню годину. Ми сумлінно полічили кількість зерен, яку бажає Сета. Число це таке велике...
Цар(гордовито). Яке велике воно не було б, житниці мої не збідніють. Нагороду обіцяно і її треба віддавати...
Старшина придворних математиків. Ти не можеш, повелителю, виконати таке бажання. У всіх твоїх коморах не має такої кількості зерна, яку зажадав Сета. Немає його і в житницях цілого царства. Не знайдеться стільки зерна і на всьому просторі Землі. І якщо неодмінно видати обіцяну нагороду, то накажи перетворити всі земні царства на поля, накажи осушити моря й океани, накажи розтопити сніги і лід, що вкривають далекі північні пустелі. Нехай увесь земний простір буде засіяно пшеницею. І все те, що виросте на цих полях, накажи віддати Сеті. Тоді він одержить свою винагороду.
Цар. (після паузи, роздумливо). Назви ж мені це дивовижне число.
Старшина придворних математиків. 18 квінтильйонів 446 квадрильйонів 844 трильйони 73 більйони 709 мільйонів 551 тисяча 615, о , повелителю!
Ведучий. Така легенда. Чи справді було, про що тут розповідалось, невідомо, але винагорода повинна була бути саме такою.
(Ілюстрація)
Ця задача вперше трапляється у хорезмського математика аль- Біруні (973-1050 р.) (портрет математика).
Вступ учнів другої групи (доповідь робить спікер ).
Задача. Найдавніша задача на прогресії - задача про розподіл хліба, записана у відомому єгипетському папірусі Рінда.
Сто мір зерна слід розподілити між п’ятьма людьми так, щоб другий одержав на стільки ж більше від першого, на скільки третій одержав більше від другого, четвертий більше від третього, п’ятий – більше від четвертого. Крім того, двоє перших повинні одержати в сім раз менше за трьох інших. Скільки потрібно дати кожному?
Розв’язання
Кількості хліба, які одержують учасники розподілу, становлять зростаючу арифметичну прогресію.
Нехай перший її член х, різниця – у, тоді:
Частина першого –х,
Частина другого- х+у,
Частина третього – х+2у,
Частина четвертого – х+3у,
Частина п’ятого –х+4у.
За умовою задачі складемо систему рівнянь:
![]()
Після спрощення система набере вигляду:
![]()
Розв’язавши цю систему , одержимо :
![]()
Відповідь. Хліб слід розділити на такі частини: ![]()
Виступ учнів третьої групи (доповідь робить спікер)
Задача про купівлю коня. (З „Арифметики” Л. Ф. Магницького).( портрет Л. Ф. Магніцького)
Деяка людина купила коня за 156 руб. Передумавши, вона почала віддавати коня назад, вважаючи, що кінь не вартий такої високої ціни. Продавець запропонував йому інший спосіб купівлі, кажучи: „ Якщо тобі здається, що ціна за коня висока, то купи тільки цвяхи, що в нього в підковах, коня ж візьми задарма. Цвяхів у кожній підкові є 6. За перший цвях дай мені полушку (1/4), а за другий – дві полушки, за третій – копійку, за четвертий – 2 копійки і т.д. Покупець, подумавши, що всі цвяхи обійдуться йому в десять рублів, захотів одержати коня в дарунок і погодився на таку купівлю. На скільки проторгувався покупець?
Розв’язання
За умовою за 6*4=24 підкови мав заплатити:
![]() копійок, що разом дорівнює
копійок, що разом дорівнює ![]() к. Отже, замість сплати початкової суми 156 руб (15 600 коп.) покупець втратив порівняно з початковою сумою
к. Отже, замість сплати початкової суми 156 руб (15 600 коп.) покупець втратив порівняно з початковою сумою
![]() (к.), що становить 41 787 руб. 3 коп. 3 полушки.
(к.), що становить 41 787 руб. 3 коп. 3 полушки.
На таких умовах продавець і коня легко дає в додачу.
Виступ учнів четвертої групи (доповідь робить спікер)
Задача. Винагорода воїна.(З російського підручника математики Є. Войтяховського, 1795 р.)
Воїну , який служив, дано винагроду: за першу рану – 1 копійку, за другу – 2, за третю -4 і т.д. Виявилось, що воїн одержав винагроду 655 руб.35 коп. Запитується, скільки в нього ран?
Розв’язання
Винагорода за кожну рану утворює геометричну прогресію. Складемо рівняння:
![]()
![]() звідки маємо:
звідки маємо:
![]()
За такої великодушної системи нагородження воїн повинен одержати 16 ран і залишитися живим, щоб „удостоїтися” нагороди 635 руб.35 коп.
Учитель.
Завдання.
Послідовності задано переліченням їх членів. Як можна задати ці послідовності формулами:
а) 1, 2, 3, 4, 5,...
б) 2, 4, 6, 8, 10,...
в)1, 3, 5, 7, 9, 11,...
г)1, 4, 9, 16, 25,...
Члени цих послідовностей – цілі числа, тому такі послідовності називають цілочисельними.
Як ви вважаєте чи багато таких послідовностей?
Чи добре вони вивчені, чи добре вони відомі?
Виявляється, що таких послідовностей багато. Усі вони дуже цікаві, але деякі з них відомі ще мало. Лише в 1973 році в США було видано довідник числових послідовностей. У ньому описано більше 2300 послідовностей, кожна під своїм номером. У цьому списку під номером 577 записано послідовність : 1, 2, 5, 14, 132, 429,...
Члени цієї послідовності називаються числами Каталана на честь бельгійського вченого Ежен Шарля Каталана, який у 1838 році описав вперше цю послідовність.
Повідомлення учня. Числа Каталана.
Першим з числами Каталана зустрівся Леонард Ейлер, розв’язуючи задачу: скількома способами можна розділити опуклий многокутник на трикутники діагоналями, що не перетинаються?

Відповіддю до цієї задачі є числа Каталана:
для трикутника – 1 спосіб,
для чотирикутника – 2 способи,
для п’ятикутника – 5 способів,
для шестикутника – 14 способів і т.д.
Числа Каталана є відповіддю і до такої задачі. Скільки існує різних шляхів тури з лівого кута в правий на шахівниці зі сторонами 2, 3, 4,...?
За допомогою чисел Каталана розв’язується багато цікавих задач, наприклад задача про рукостискання.
За круглим столом сидить парна кількість осіб. Кожний потискує руку іншому так, щоб ніякі дві пари не перетинались. Скількома способами це можна зробити ?
( Зручно продемонструвати учням розв’язання задачі для двох і чотирьох осіб практично). Для шести – демонстрація - малюнок.
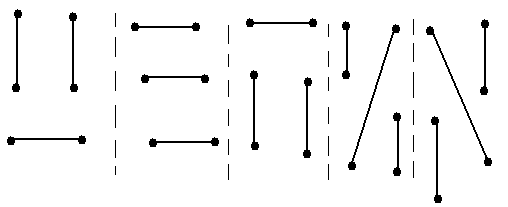
Повідомлення учня. Числа Фібоначчі.
Іншим прикладом цілочислової послідовності є послідовність Фібоначчі:
1, 1, 2, 3, 5, 8, 13, 24,..., названої на честь Леонардо Пізанського, відомого ще як Фібоначчі. Його творчість вплинула на розвиток алгебри і теорії чисел, зокрема, на дослідження таких видатних математиків, як Франсуа Вієт і П’єр Ферма.
Леонардо народився у великому італійському місті-республіці Пізі. Невдовзі після народження сина, батька направили зі службовими дорученнями до Алжира, де він виконував обов’язки близькі до консульських. Пізніше туди переїхав і Леонардо.
Фібоначчі відвідав Єгипет, Сирію, Грецію, Сицилію, Прованс і скрізь цікавився математичними працями різних учених. Повернувшись до Пізи, він серйозно зайнявся математикою. Ознайомившись з „Началами” Евкліда, і поєднавши ці знання з тим, про що Леонардо довідався від арабських учених, він видав у 1202 році „Книгу абака” – справжню енциклопедію математичних знань своєї епохи. У цій книзі вперше наведено розв’язання відомої задачі про кроликів.
Запитується, скільки пар кролів народиться від однієї пари за рік, якщо кожна пара приносить щомісяця по одній парі, у свою чергу здатній через місяць до розмноження, і якщо кожна пара не загине.
Відповідь до задачі виражається сумою ряду 1+1+2+3+5+8+13+...+144. Кожний член попереднього ряду, починаючи з третього , є сумою двох попередніх:
![]() .
.
Цю послідовність пізніше почали називати послідовністю Фібоначчі.
Наведемо розв’язання задачі про кролів. Введемо позначення:
пару кролів, яка народжує, позначатимемо так;
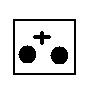
А пару кролів, яка не народжує, так:
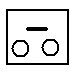
Кожна пара, яка народжує, через місяць дає саму себе і нову пару, що не народжує. Через місяць пара, яка не народжує, переходить у розряд тих, що народжують, але не дає нової пари. Випишемо послідовність кількості пар кролів на початку кожного з шести місяців: 1,2, 3,5,8,13.
Використовуючи залежність, що кожний член, починаючи з третього, дорівнює сумі двох попередніх членів, продовжимо ряд до тринадцятого члена: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377. Це і буде відповіддю до задачі, поставленої Фібоначчі.
Ряд Фібоначчі згодом виявився дуже корисним у науці. Він зустрічається в багатьох розділах математики: у комбінаториці, в теорії чисел, геометрії, а також задачах на максимум та мінімум.
Він відомий не тільки в математиці, а й в природознавстві.
Якщо дерево розгалужується щороку і на другому році 2 гілки, то на третьому кількість гілок, звичайно, доходить до 3, на четвертому – до 5, п’ятому – до 8, і так щороку. Отже, кількість гілок є послідовністю чисел Фібоначчі.
Листя на гілках росте навколо стебла рівномірно за гвинтовою лінією, тобто кожний наступний листок знаходиться вище і вбік від попереднього. При цьому для кожного виду рослин характерний свій кут розходження сусідніх листків. Так, у липи і в’яза він становить![]() частини кола, у бука -
частини кола, у бука - ![]() , у дуба і вишні -
, у дуба і вишні - ![]() , у тополі і груші -
, у тополі і груші - ![]() , у верби -
, у верби - ![]() тощо. Такий самий кут зберігається у кожного виду рослин і в розташуванні гілок, бруньок, лусочок у середині бруньок, а також у квітів.
тощо. Такий самий кут зберігається у кожного виду рослин і в розташуванні гілок, бруньок, лусочок у середині бруньок, а також у квітів.
Найпоширеніші серед рослин такі кути розходження ( у частинах кола) :
![]() Ряди чисельників та знаменників – це послідовності Фібоначчі.
Ряди чисельників та знаменників – це послідовності Фібоначчі.
Виступ учнів п’ятої групи (доповідь робить спікер).
Вправа. Чи можуть числа ![]() бути членами однієї арифметичної пргресії?
бути членами однієї арифметичної пргресії?
Розв’язання
І спосіб.
Якщо числа ![]() є членам арифметичної прогресії, то
є членам арифметичної прогресії, то ![]() є середнім арифметичним між
є середнім арифметичним між ![]() і
і![]() , тобто
, тобто ![]() . Піднесемо до квадрата обидві частини рівності:
. Піднесемо до квадрата обидві частини рівності:
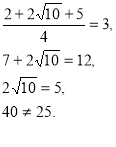
Отже, дані числа не утворюють арифметичну прогресію.
ІІ спосіб.
Якщо дані числа утворюють арифметичну прогресію, то ![]() , де
, де ![]() тоді
тоді
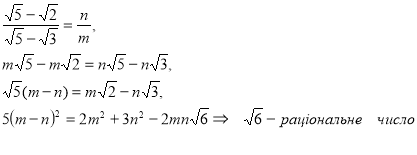
Дістали протиріччя. Отже, числа ![]() не можуть бути членами однієї арифметичної прогресії.
не можуть бути членами однієї арифметичної прогресії.
Вступ учнів шостої групи (доповідь робить спікер ).
Вправа. Розв’язати рівняння
![]() де х –ціле число.
де х –ціле число.
Розв’язання
Помножимо обидві частини цього рівняння на х, маємо:
(х-1)+(х-2)+(х-3)+...+1=3х.
Ліва частина цього рівняння – сума членів арифметичної прогресії, де 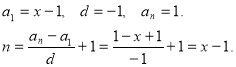
Оскільки ![]()
![]()
Відповідь: х=7.
Вступ учнів сьомої групи (доповідь робить спікер ).
Вправа. Розв’язати рівняння:
![]()
Розв’язання
Доданки даного рівняння утворюють арифметичну прогресію, у якої ![]()
Тоді
![]() . З іншого боку
. З іншого боку ![]() . Отже,
. Отже,
![]()
![]()
Корені цього рівняння , а отже, і початкового :![]()
Вступ учнів восьмої групи (доповідь робить спікер ).
Вправа. Розв’язати рівняння:
![]()
Розв’язання
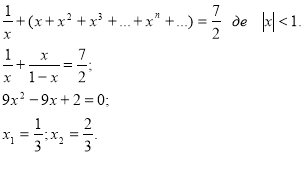
Вступ учнів дев’ятої групи (доповідь робить спікер ).
Вправа. Знайти суму S =1-2+4-8+16-32+64-128+256-512.
Розв’язання
S =1-2 (1-2+4-8+16-32+64-128+256);
S =1-2 ( S+512);
3S =-1023;
S =-341.
Підведення підсумків виступів. Слово надається журі
Заключне слово вчителя. Цінування підготовки учнів до уроку.


про публікацію авторської розробки
Додати розробку
