Урок-узагальнення знань "Ознаки подібності трикутників"

Тема. Ознаки подібності трикутників. Розв’язування  задач і вправ.

Мета:  навчальна: узагальнити, систематизувати знання учнів про зміст ознак подібності трикутників та виокремити приклади застосування ознак подібності трикутників; відпрацювати навички застосування ознак ;розвивальна: розвивати логічне мислення, вміння висловлювати свою думку, вміння обгрунтовувати, слухову та зорову пам’ять, увагу; вихована: виховувати позитивне ставлення до математики, працьовитість, кмітливість.

Тип уроку: застосування знань, вмінь і навичок учнів.

Хід уроку

І. Організаційний момент.

Вчитель. Доброго дня, діти. Свій урок я хочу розпочати зі слів відомого математика Піфагора: «Добре засвоєна мудрість не забувається ніколи.» Тому пропоную сьогодні ще раз узагальнити свої знання та вміння застосовувати ознаки подібності на практиці. Зокрема і в повсякденному житті. Як? А давайте уявимо собі таку ситуацію: ми вирішили усім класом зустріти Новий рік. Але для святкової атмосфери нам необхідна ялинка. Отож, ми вирушаємо за ялинкою. Усе навкруги вкрито білим пухнастим снігом, сонечко весело всміхається, ніби вже вітає вас із настанням Нового року. Прийшовши в магазин, ми побачили найвищу ялинку, і вирішили її прикрасити гірляндами і, головне, яскравою зіркою. Знаючи свої фізичні можливості: піднятися на дерево не вище, ніж 5 м, ми зрозуміли, щоб не витрачати даремно зусиль і не везти ялинку в школу, потрібно спочатку визначити, чи можливо це зробити.

Отже, перед нами стоїть задача – як виміряти висоту ялинки? Метою нашого уроку є вчитися застосовувати ознаки подібності трикутників до розв’язування задач. І я сподіваюсь, що в кінці уроку ви зможете вирішити цю проблему.

І почнемо роботу ми  з перевірки домашнього завдання.

ІІ. Перевірка домашнього завдання.

Для перевірки теоретичних та практичних навичок по даній темі пропоную вам пройти тест за посиланням: https://learningapps.org/1983270 Його я вам завантажила у спільну групу. Результати виконаних завдань повідомлю вкінці уроку.

IІІ. Актуалізація опорних знань.

Вчитель.  А тепер давайте разом пригадаємо теоретичний матеріал який ми вивчали на попередніх уроках.

Фронтальна бесіда.

1.                   Які трикутники називаються подібними?
2.                   Сформулюйте першу ознаку подібності трикутників.
3.                   Сформулюйте другу ознаку подібності трикутників.
4.                   Сформулюйте третю ознаку подібності трикутників.
5.                   Якщо в трикутнику проведено, пряму паралельну третій стороні, то що можна сказати про отримані трикутники?
6.                   Чи подібні два трикутники, якщо сторони одного трикутника дорівнюють 2 м, 3м і 4м, а другого – 3 м, 4м і 5 м?

Вчитель. Ще раз хочу нагадати, що саме узагальнена теорема Фалеса була покладена в основу вивчення подібності фігур, що дало змогу розв’язати багато практичних задач.

IV. Розв’язування задач.

У вас на парті є картка на якій представлено задачі за готовими малюнками. Двоє учнів йдуть до дошки і навипередки розв’язують дані задачі. Всі інші самостійно в зошитах. Перші три учні які правильно і найшвидше виконають завдання отримають додаткові бали.

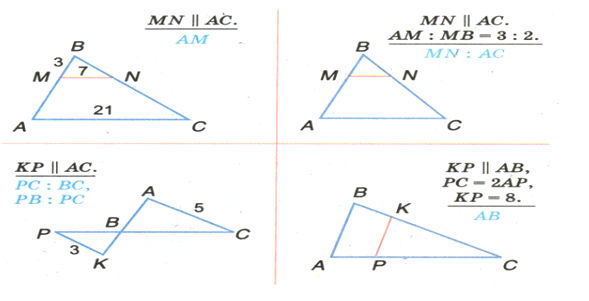
2. Розв’язуємо задачі прикладного змісту.

Завдання 1. З допомогою фотографії виміряти висоту вежі.

Розв'язання.

Висота вежі відноситься до довжини основи так як висота трикутника на фото до основи трикутника. Нехай висота вежі, то

.

В-дь: 28 м.

Яку саме ознаку подібності трикутників використано в цій задачі?

Завдання 2.   (Задача Фалеса) Визначте відстань від берега до корабля в морі, знаючи висоту щогли 20 м, довжину великого пальця - см, відстань від очей до руки – 60 см 

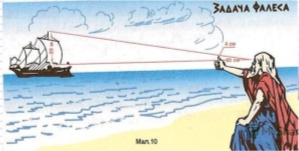Розв’язання:

Нехай х – відстань до корабля.

Відповідь: відстань від берега до корабля становить 300 м.

Яку саме ознаку подібності трикутників використано в цій задачі?

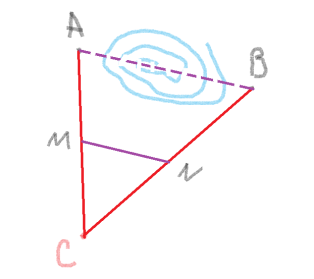
Завдання 3. Знайти відстань між двома об’єктами, до яких можна підійти, але між якими знаходиться перешкода.

Розв'язання.

Вибираємо точку С так, щоб А, В, і С не лежали на одній прямі і проводимо прямі АС і ВС. Виимірюємо відрізки АС і АВ.

Потім відкладаємо відрізки СМ і СN, зменшивши відрізки АС і СВ у одному і тому ж відношенні k, яке є коефіцієнтом подібності.

Тоді , і з подібності трикутників АВС і МNС. k=. З цього маємо АВ=.

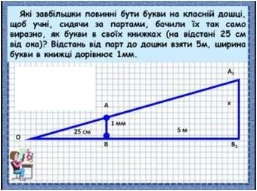
Завдання 4 Потрібно виміряти висоту дерева для встановлення сигнального прапорця. Під руками – лінійка, мотузка.

Хлопчик хоче виміряти висоту дерева. користуючись лінійкою завдовжки 15 см. На стовбурі він позначає точку, що знаходиться на відстані 1,5 м від землі. Відійшовши від дерева на 9м, хлопчик простягає перед собою руку з лінійкою так, щоб вона закривала собою дерево від верхівки до раніше вибраної точки на стовбурі. Потім він вимірює відстань АВ від ока до лінійки (наприклад за допомогою мотузки) та обчислює висоту дерева h за такою формулою: h=9∙∙ +1,5. Обгрунтуйте правильність цієї формули. В яких одиницях треба вимірювати відстань АВ? В яких одиницях тоді буде виміряно висоту дерева? Якою буде висота дерева. якщо АВ=20см?

А тепер давайте повернемося до поставленого на початку уроку запитання: як виміряти висоту ялинки? (відповіді учнів).

Можливий варіант:  у лісі можна знайти будь-яку жердину і ввіткнути її в землю. Дочекатися, коли тінь від ялинки співпаде с тінню від жердини. Тоді ми розглядаємо відношення і знаходимо висоту ялинки.

Подібна задача була запропонована випускникам на ЗНО у 2009 році. (Рисунок)

 Також існує історичний факт, що Фалес вимірював висоту піраміди за допомогою жердини. Про це можна знайти в довідковій літературі.

V. Релаксація.

Ви вже мабуть втомилися. Тому пропоную трішки відпочити і звільнитися від втоми. Для цього виконаємо наступну вправу.

V. Підведення підсумків.

Отже, на початку уроку була запропонована проблемна ситуація, яку ви успішно вирішили під час уроку. Можна зробити висновок, що використовуючи ознаки подібності трикутників ми можемо розв’язати ряд практичних задач.

VI. Домашнє завдання.

Повторити ознаки подібності,

Розв'язати задачі.

1. У рівнобедреному трикутнику ABC з основою АС кут В дорівнює 36°, AD — бісектриса трикутника. Доведіть, що ΔАВС ~ ΔCAD.

2. Одна з діагоналей трапеції дорівнює 28 см і ділить другу діагональ на відрізки довжиною 5 см і 9 см. Знаючи, що менша основа трапеції дорівнює 6 см, знайдіть:

а) відрізки, на які точка перетину діагоналей ділить першу діагональ;

б) бічну основу трапеції.

3. Розв’язати задачу за малюнком.