Урок в 10 класі на тему: "Рівняння sin x = b"

Тема уроку:. Рівняння sin х = b.

Мета уроку: Засвоєння учнями виведення і застосування фор­мули для коренів рівняння sin x = b.

Обладнання: Таблиця «Рівняння sin х = b».

І. Перевірка домашнього завдання.

1. Відповіді на питання, що виникли при виконанні домашніх завдань.

2. Самостійна робота.

Варіант 1

Розв'яжіть рівняння:

а) 2cos = . (3 бали)  б) 2cos²x + cos x – 1 = 0. (3 бали)

в) 4cos x = 4 – sin x. (3 бали)  г) sin 3х sin x – cos 3х cos x = . (3 бали)

Варіант 2

Розв'яжіть рівняння :

а) 2 cos = . (3 бали)  б) 2cos²x – cosx – 1 = 0. (3 бали)

в) 8 sin²х + cosx + 1 = 0. (3 бали)  г) sin² - cos² = 1. (3 бали)

Відповідь:

B-l. a)±+4πn, nZ; б) ±+2πn і π+2πn, nZ; в)2πn, nZ; г) ±+πn,nZ.

В-2. a) ±+,nZ; б) 2πn і ±+2πn, nZ; в) п+2πn, nZ; т) 4πn,nZ.

II. Повідомлення теми уроку.

III. Сприймання і усвідомлення матеріалу про розв'язування рівняння sin х = b.

.      Пояснення вчителя

Оскільки областю значень функції y = sin x є проміжок [–1; 1], то при | b | > 1 рівняння sin x = b не має розв’язків. Разом з тим при будь-якому b такому, що b ≤1, це рівняння має корені, причому їх безліч. Зазначимо, що окремі випадки рівняння sin x = b (для b = 1, b = 0, b = –1) було розглянуто раніше (див. п. 17).

Для того щоб отримати загальну формулу коренів рівняння sin x = b, де b 1, звернемося до графічної інтерпретації.

На рисунку 28.1 зображено графіки функцій y = sin x і y = b, b 1.

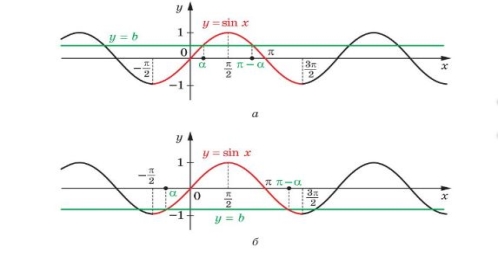
Розглянемо функцію y = sin x на проміжку – [], тобто на проміжку, довжина якого дорівнює періоду цієї функції (червона частина кривої на рисунку 28.1). На цьому проміжку рівняння sin x = b має два корені. Позначимо корінь, який належить проміжку −  [] , через . Оскільки sin (π – a) = sin α, то другий корінь дорівнює  π – α. Зауважимо, що при

 b = 1 корені α і  π – α збігаються та дорівнюють

Оскільки функція y = sin x є періодичною з періодом 2 π, то кожен з інших коренів рівняння sin x = b відрізняється від одного зі знайдених коренів на число виду 2 π n, n ∈ Z . Тоді корені рівняння sin x = b можна задати формулами x = a + 2 π n і x =  π – a + 2 π n, n ∈ Z. Ці дві формули можна замінити одним записом: x = (–1)ka + π k, k ∈. (1) Справді, якщо k — парне число, тобто k = 2n, n ∈ Z, то отримуємо: x = a + 2πn; якщо k — непарне число, тобто k = 2n + 1, n ∈ Z, то отримуємо: x = –a +π  + 2 πn = π – a + 2πn. Формула (1) показує, що корінь a відіграє особливу роль: знаючи його, можна знайти всі інші корені рівняння sin x = b. Корінь a має спеціальну назву — арксинус.

 Означення. Арксинусом числа b, де b m 1, називають таке число a з проміжку – []; , синус якого дорівнює b. Для арксинуса числа b використовують позначення arcsin b.

Розглянемо приклади.

Приклад 1. Розв'яжіть рівняння sinx = .

Розв'язання

Згідно з формулою (1) маємо: х = (-1)ⁿ arcsin + πп, п Z.

Оскільки arcsin = , то х = (-1)ⁿ + πn, п є Z.

Відповідь: (-1)ⁿ + πn, п є Z.

Приклад 2. Розв'яжіть рівняння sin х = - .

Розв'язання

Згідно з формулою (1) маємо: х = (-1)ⁿ arcsin + πп, п Z.

Оскільки arcsin = - , то х =(-1)ⁿ ·+ πn, nZ; х = (-1)ⁿ⁺¹ + πп, п Z.

Відповідь: (-1)ⁿ⁺¹ + πп, п Z.

Приклад 3. Розв'яжіть рівняння sin x = – 1.

Розв'язання

Згідно з формулою (1) маємо: х = (-1)ⁿ arcsin(– 1) + πп, пZ.

Значення arcsin(-1) знайдемо за допомогою мікрокальку­лятора:

arcsin(– 1) 0,427, тоді х (-1)ⁿ · 0,427 + πn, п Z.

Відповідь: (-1)ⁿ · arcsin(-1) + πп (-1)ⁿ · 0,427 + πп, п Z.

IV. Осмислення вивченого матеріалу.

Коментоване виконання вправ

V. Підведення підсумків уроку.

1. При яких значеннях b має корені рівняння sin x = b?

2. Скільки коренів має рівняння sin x = b при b ≤ 1?

3. Що називають арксинусом числа b?

4. Запишіть формулу коренів рівняння sin x = b при b ≤ 1.

VI. Домашнє завдання.

Розділ IV § 28. Вправи № 28.4; 28.6; 28.10.