Тема уроку:  Рівняння cos х = b.

Мета уроку: Засвоєння учнями виведення і застосування фор­мули для знаходження коренів рівняння cos x =b.

Обладнання: Таблиця «Рівняння cos x = b».

І. Перевірка домашнього завдання.

Математичний диктант

Обчисліть:

1) arcsin ;  2) arcos ;       3) arctg ;  4) arcsin;

5) arccos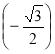;  6) arctg (-l);      7) arcctg (-l);  8) cos (arсcos l);  

9) sin ; 10) arcsin ; 11) arccos ;  12) arccos .

Відповіді:

1) ; 2) ; 3) ; 4) -; 5) ; 6) -; 7) ; 8)1; 9) ; 10) ; 11) ; 12) .

II. Мотивація навчання та повідомлення теми уроку.

Усім відомо, що квадратні рівняння можна розв'язувати за допомогою формули їх коренів, що значно спрощує роботу.

У математиці розглядають рівняння, у яких невідоме (змінна) входить тільки під знак тригонометричних функцій, наприклад:

cos x = 1, cos x + sin x = 0. Ці рівняння називаються тригономет­ричними рівняннями. Як правило, розв'язування будь-якого тригонометричного рівняння зводиться до розв'язування най­простіших рівнянь: sin x = b, cos x = b, tg x = b,   ctg x = b.

Отже, наше завдання — вивести формули для розв'язування найпростіших тригонометричних рівнянь і навчитися розв'язува­ти тригонометричні рівняння, які приводяться до найпростіших.

На сьогоднішньому уроці розглянемо розв'язування рівнян­ня cos x = b.

ІІІ. Сприймання і усвідомлення матеріалу про розв'язування рівняння    cos x = b.

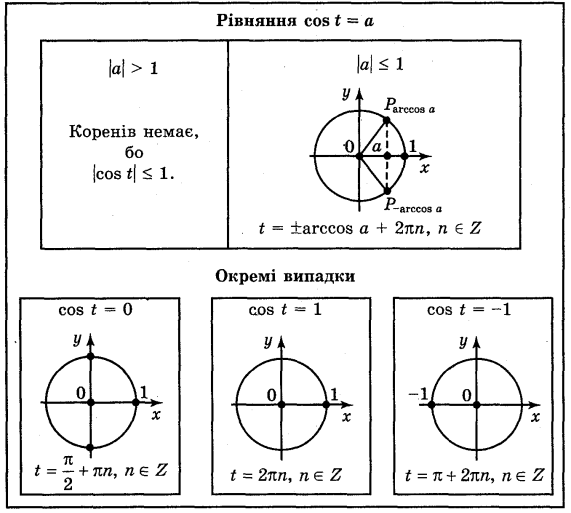
Демонструється таблиця 8.

Пояснення вчителя

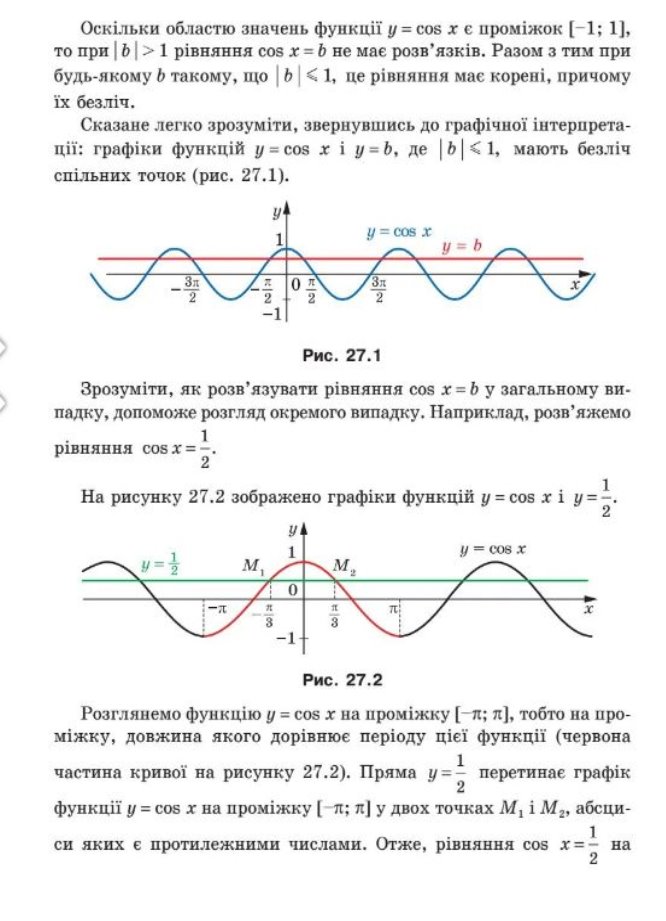
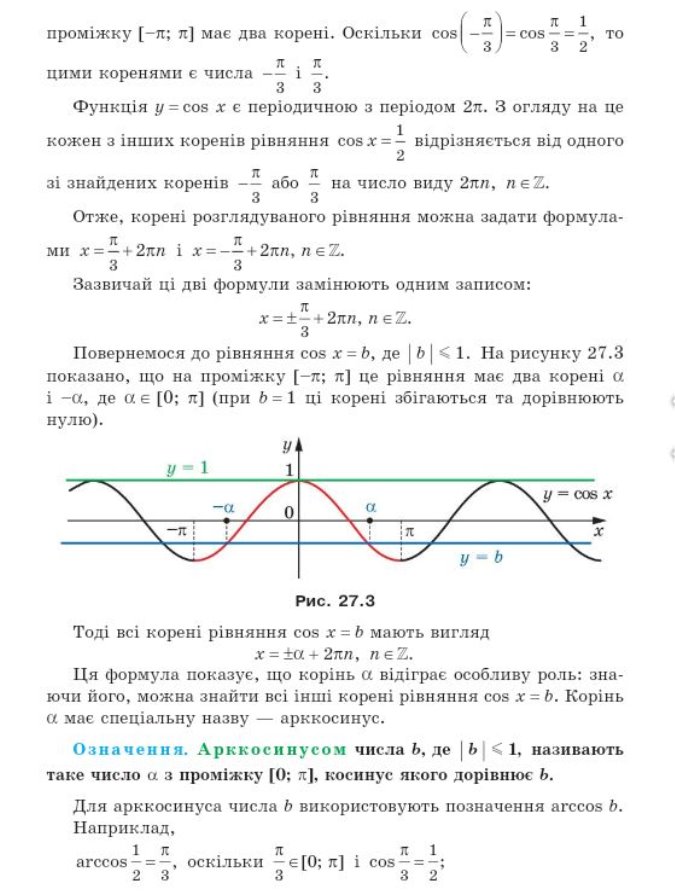
Приклад 1. Розв'яжіть рівняння cos x = .

Розв'язання

Згідно з формулою (1) маємо:

х = ± arccos + 2πn, п Z.

Оскільки arccos = , то маємо:  х = ± + 2πп, п є Z.

Відповідь: ± + 2πп, п Z.

Приклад 2. Розв'яжіть рівняння cos x = .

Розв'язання

Оскільки > 1, то рівняння коренів не має.

Відповідь: коренів немає.

Приклад 3. Розв'яжіть рівняння cos x = 0,37.

Розв'язання

Згідно з формулою (1) маємо:

х = arccos 0,37 + 2πп, п Z.

Значення arccos 0,37 знайдемо за допомогою мікрокалькуля­тора:         arccos 0,37 1,19, тоді х ± 1,19 + 2πn, n Z.

Відповідь: arccos 0,37 + 2πn ± 1,19 + 2πn, n Z.

Приклад 4. Розв'яжіть рівняння cos x = -.

Розв'язання

Згідно з формулою (1) маємо: х = ±arccos 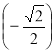+ 2πп, п Z.

Оскільки arccos 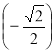= π - arccos = π - = , то

x = ± + 2πn, n Z.

Відповідь: ± + 2πn, n Z.

IV. Осмислення вивченого матеріалу.

Виконання вправ

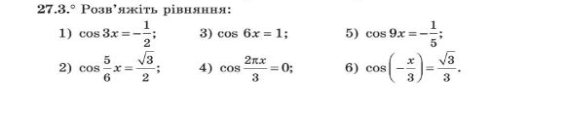
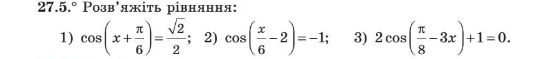
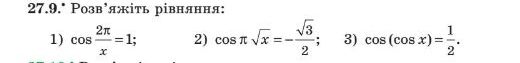
V. Підсумок уроку.

1. При яких значеннях b має корені рівняння cos x = b?

2. Скільки коренів має рівняння cos x = b при b ≤ 1?

3. Що називають арккосинусом числа b?

4. Запишіть формулу коренів рівняння cos x = b при b ≤ 1.

VI. Домашнє завдання.

Розділ IV § 27. Вправи № 27.4; 27.6;27.10

Таблиця 8