Урок в 6 класі. Координатна площина

Тема. Координатна площина.

Мета уроку: навчити учнів будувати точку за її координатами і визначати координати точки, позначеної на координатній площині

Задачі уроку:

•              ознайомити учнів з прямокутною системою координат на площині;
•              навчити орієнтуватися на координатній площині, чітко і акуратно виконувати геометричні побудови;
•              розвивати творчі здібності;
•              виховувати інтерес до предмету

Типуроку: вивчення нового матеріалу

Обладнання: робочий зошит, лінійка, олівець, картки із завданням.

Щоб щось пізнати,

Треба вже щось знати

Станіслав Лем

Хідуроку

1.                 Організаційний момент

Перевірка наявності всіх потрібних інструментів і навчальних посібників для уроку

II. Оголошення теми, мети і плану уроку

Учні записують в зошитах дату проведення уроку, вид роботи (класна робота), тему уроку: «Координатна площина».

ІІІ. Мотивація навчальної діяльності

Звертаю вашу увагу на епіграф нашого уроку: « Щоб щось пізнати, треба вже щось знати». Ми вже знаємо, як визначати положення точки на прямій і це допоможе нам пізнати,  як визначати положення точки на координатній площині.

Звертаючись один до одного, люди часто говорять: «Залиште свої координати». Для чого? Щоб людину можна було легко знайти. Це може бути: номер вашого телефону, домашня адреса, місце роботи.

ІІ. Повторення вивченого матеріалу

Які прямі називаються паралельними?

Які прямі називаються перпендикулярними?

Визначить на ваш погляд, які прямі перпендикулярні? Паралельні? Яким інструментом можна перевірити ваші відповіді?

        c            d

 

a

 

 

 

b

                                               m            

                                                             n

1.          Яка пряма називається координатною?
2.          Якими числами визначаються координати точок, розташованих справа від початку координат? Зліва від початку координат?
3.          Яку координату має початок координат?
4.          Скільки чисел визначають положення точки на координатній прямій?

Назвіть координати точок, зображених на рисунку. Як записати їх координати?

                    R          P            A   O           K           C         L

                                                                                                 х

                                            -1   0   1      

 

III. Вивчення нового матеріалу

Суть системи координат полягає в тому, що це правило, за яким визначають положення об’єкта. Системи координат оточують нас усюди. Наприклад, ми купили квиток до кінозалу. Там обов’язково вказано ряд і місце. Приведіть ще подібні приклади:

•              система географічних координат (широта-паралелі і довгота - меридіани);
•              шахова дошка;
•              поле для гри «Морський бій»;
•              географічні та зоряні карти;
•              координатна сітка для пілотів, моряків…

(відповіді супроводжуються показом рисунків). 

Ми з’ясували, що системи координат оточують практичне життя людини. Ідея координат зародилася в стародавні часи в зв’язку з потребою астрономії, географії, живопису. Математика як наука виникла зі спостережень за навколишнім світом і потреби визначити закономірності цього навколишнього світу мовою чисел.

Використовувати координати в математиці вперше почав П’єр Ферма (1601-1665) і французький філософ, математик Рене Декарт (1596-1650). В 1637 році вийшла книга Рене Декарта «Міркування про метод». В ній він запропонував новий метод – метод координат, який дозволив переходити від точки в координатній площині до пари чисел – її координат. Система координат дозволяє визначити положення того чи іншого об’єкту. На честь Декарта прямокутну систему координат називають ще прямокутною декартовою системою координат.

Що ж таке система координат?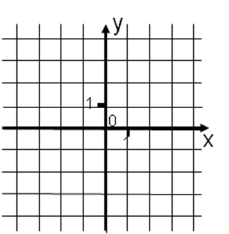

Накреслимо дві перпендикулярні прямі-осі координат, вкажемо на них додатні напрямки, початок координат, одиничний відрізок 1 клітина.

Прямі х і у називають осями координат, точку О – початком координат. Горизонтальну координатну пряму називають віссю абсцис і позначають буквою  х, вертикальну координатну пряму називають віссю ординат і позначають буквою у. Прямі кути, отримані осями координат називаються координатними кутами-чвертями  (І, ІІ, ІІІ, ІV) або квадрантами.                                                       

Положення точки на координатній площині визначається парою чисел (х;у), які називаються координатами точки. Першу координату точки називають абсцисою точки, а другу координату-ординатою.  І навпаки, кожній парі чисел (х;у) відповідає тільки одна точка на площині.

Координати точки записуємо в дужках через крапку з комою, причому першою завжди записують координату х, другою-координату у. А не навпаки: «Не став воза попереду коня».

IV. Закріплення нового матеріалу

Вправа 1.

А зараз ми з вами за координатами знайдемо точки (0;0), (-3;-1), (-4;-4), (-4;-8), (-6;-10), (-6; -8), (-5;-7), (-5;-1), (-3;1), (-1;2), (-2;3), (-3;5). Послідовно з’єднаємо точки відрізками. Після виконання завдання отримали частину малюнка. Добудуйте його на свою уяву.

Вправа 2.

Робота в парах

А зараз самостійно побудуйте одне з зоряних сузір  (у кожної групи  на столі лежить конверт з написом назви сузір’я:  Цефея, Кассіопеї, Андромеди, Персея,Кита, Пегаса )

 

Сузір’я Цефея                                                               Сузір’я Кассіопеї

(0;5), (-1;4), (-2;1), (1;-1), (6;-1), (3;2)                    (-5;0), (-3;2), (-1;0), (1;0), (3;-2)

Сузір’я Андромеди                                                                        Сузір’я Персея

(-2;9), (0;7), (1;4), (2;-2),                                                   (-5;-3), (-2;-2), (0;-1), (2;-2), (4;-1),

 (-2;-1),(-2;5), (-4;4), (5;0), (6;2), (0,5;1), (1;3)       

Сузір’я Кита                                                                                     Сузір’я Пегаса

(11;-7), (9;-6), (10;-5), (7;-1), (4;-1), (2;0),                                 (-6;8), (-4;9), (0;7), (1;5), (8;5), (8;-2), (-3;0), (0;3), (6;1), (9;2)                                                          (0;-1), (-2;-4), (-2;-2)

Вправа 3.

1. (-8;1), (-6;2); (-2;0);(1;2);(5;1);(7;-4);(9;-3).
2. (-2;6),(0;8),(3;7);(5;5),(7;7).
3. (1;2).(3;9),(4;8),(5;8);(6;9),(6;10),(5;11),(4;11),(3;10),(3,9)

Робота з підручником

VІІ. Підсумок уроку.

Дидактична гра «Згадати все»

Учні по черзі проговорюють всі основні поняття теми.

         ІХ. Рефлексія.

- Чи сподобався вам урок?

Діти показують свій емоційний стан після уроку, зображуючи "смайлик",  відповідний до їх  настрою.  

VІІІ. Домашнє завдання Виконати творчу роботу на координатній площині

 

 

 

 

 

 

 

 

 

 

Виконати творчу роботу на координатній площині. Побудова малюнків за даними координатами точок

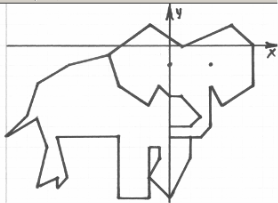                                          Картка 1

 (-6;-1), (-5;-4), (-2;-6), (-1;-4), (0;-5), (1;-5), (3;-7), (2;-8), (0;-8), (0;-9), (3;-9), (4;-8), (4;-4),  (5;-6), (8;-4), (8;0), (6;2), (4;1), (0;1), (-2;2), (-6;-1),

(-10;-2), (-13;-4), (-14;-7), (-16;-9),(-13;-7),

 (-12;-10), (-13;-14),(-10;-14), (-10;-13),

 (-9;-13), (-10;-9), (-5;-9), (-5;-15), (-2;-15),

(-2;-13). (-2;-10), (-1;-10), (-1;-11), (-2;-13),

(0;-15), (2;-11), (2;-9).

 

 

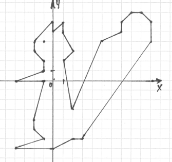                                                  Картка 2

 

(-2;4),(0;6), (0;5), (1;6), (1;5), (2;3), (1;2), (2;-3), (5;4), (7;5), (7;6), (8;7), (9;7), (10;6), (10;4), (3;-6), (2;-6), (0;-7), (-4;-7),

 (-1;-6), (-2;-5), (-2;-4), (-1;0), (-4;0), (-1;1), (-1;2), (-2;3), (0;4).

 

 

 

 

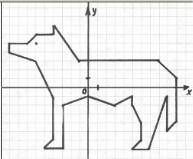
                                       Картка 3

 (- 9; 5), (- 7; 5), (- 6; 6), (- 5; 6), (- 4; 7), (- 4; 6), (- 1; 3),

(8; 3), (10; 1), (10; - 4), (9; - 5), (9; - 1), (7; - 7), (5; - 7),

(6; - 6), (6; - 4), (5; - 2), (5; - 1), (3; - 2), (0; - 1), (- 3; - 2),

 (- 3; - 7), (- 5; - 7), (- 4; - 6), (- 4; - 1), (- 6; 3), (- 9; 4),(-9;5).

 

 

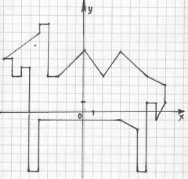
                                             Картка 4

 

(- 9; 6), (- 5; 9), (- 5; 10), (- 4; 10), (- 4; 4), (- 3; 4), (0; 7),

 (2; 4), (4; 7), (7; 4), (9; 3), (9; 1), (8; - 1), (8; 1), (7; 1),

(7; - 7), (6; - 7), (6; - 2), (4; - 1), (- 5; - 1), (- 5; - 7),(- 6; - 7), (- 6; 5), (- 7;5), (- 8; 4), (- 9; 4), (- 9; 6).

 

 

 

 

 

 

 

 

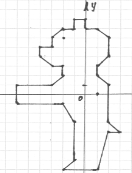                                                                       Картка 5

 

 (-4;5), (-3;5), (-3;6), (-2;7), (-1;7), (-1;8), (0;8), (0;7), (1;7), (2;6), (2;4), (1;3), (1;2), (2;1), (2;-3), (3;-4), (2;-4), (1;-8), (-2;-8), (-1;-7), (-1;-3),

 (-2;-1), (-6;-1), (-3;1), (-2;2), (-2;3), (-3;3), (-4;4). 

 

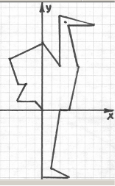
                                                               Картка 6

 

(0; 0), (- 1; 1), (- 3; 1), (- 2; 3), (- 3; 3), (- 4; 6), (0; 8), (2; 5), (2; 11),

(6; 10), (3; 9), (4; 5), (3; 0), (2; 0), (1; - 7), (3; - 8), (0; - 8), (0; 0).

 

 

 

 

 

 

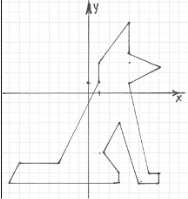
                                                      Картка 7

(- 8; - 9), (- 6; - 7), (- 3; - 7), (1; 1), (1; 3), (4; 7), (4; 4),

(7; 2,5),(4; 1), (6; - 8), (7; - 8), (7; - 9), (5; - 9), (3; - 3),

(1,5; - 6), (3; - 8), (3; - 9), (- 8; - 9).

 

 

 

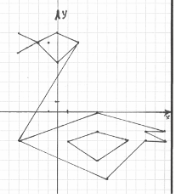
                                                   Картка 8

 

1) (2; 7), (0; 5), (- 2; 7), (0; 8), (2; 7), (- 4; - 3), (4; 0), (11; - 2),

    (9; - 2), (11; - 3), (9; - 3), (5; - 7), (- 4; - 3).

2) Клюв: (- 4; 8), (- 2; 7), (- 4; 6).

3) Крило: (1; - 3), (4; - 2), (7; - 3), (4; - 5), (1; - 3).

 

 

 

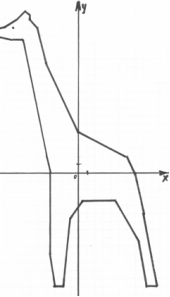
                                                        Картка 9

 

(-2;-14), (-3;-14), (-3,5;-10), (-3,5;0), (-4;2), (-7;16,5), (-8;16,5), (-11;17), (-11;17,5), (-9;18), (-7,5;19),

 (-6,5;20), (-6;19,5), (-6;19), (-5;18), (-4;13,5), (0;5), (6;3), (8;0), (6;2), (7;0), (8;-5), (9,5;-14), (8,5;-14), (7,5;-8,5), (4,5;-3,5), (0,5;-3,5), (-1;-5,5), (-1,5;-9),

 (-2;-14).