Урок "Властивості функцій."

Тема:  Властивості функцій

Мета. Узагальнити й систематизувати знання студентів про функції та     

  їх графіки, ознайомити студентів з властивостями функцій.

Тип заняття. Засвоєння нових знань.

Обладнання. підручники Г.П.Бевз, В.Г.Бевз Математика 10,  

                       М.І.Шкіль, З.І.Слєпкань, О.С.Дубинчук Алгебра і 

                       початки аналізу, таблиці, роздатковий матеріал, 

                        креслярські  приладдя, мультимедійний комплекс.

 

Інтерес до учіння - важливий стимул

 навчальної діяльності учнів.

В. О. Сухомлинський

 

Хід заняття

І. Перевірка домашнього завдання.

Фронтальне опитування студентів.

1) Дайте означення функції.

Відповідь. Функцією називають таку відповідність між змінними х і у, при якій кожному значенню змінної х відповідає єдине значення змінної у.  При  цьому змінну х називають аргументом, а змінну у функцією (від аргументу х).

2) Що таке область визначення функції?

Відповідь. Усі значення, яких набуває аргумент утворюють область визначення функції і позначають D(у).

3) Що таке область значень функції?

Відповідь. Усі значення, яких набуває залежна змінна утворюють область зна­чень функції і позначають Е(у).

4) Які способи задання функції вам відомі?

Відповідь. Задавати функції можна формулами, таблицями, графіком.

5) Що таке графік функції?

Відповідь. Графіком функції називається фігура, яка складається з усіх точок координатної площини, абсциси яких дорівнюють значенню аргументу, а ордина­ти - відповідним значенням функції.

 

ІІ. Мотивація навчальної діяльності. Сприймання і усвідомлений нового матеріалу.

Функції відрізняються одна від одної не тільки областями визначення й зна­чень, а й іншими властивостями. Деякі з властивостей ми вивчимо на цьому занятті.

1. Розв'яжемо вправу. Знайдіть координати точки перетину графіка функції           у = -Зх + 9 з віссю абсцис; віссю ординат.

 Розв 'язання.

Абсциси точок перетину графіка функції з віссю абсцис знаходимо розв'язавши рівняння f(х) = 0.

 -Зх + 9 = 0,

 -Зх = -9,

х = 3

(3;0) - точка перетину з Ох .

Ординату точки перетину графіка функції з віссю ординат знаходимо, обчислив­ши  f(0).

(0;9) - точка перегину з Оy.

Абсциси точок перетину графіка функції з віссю абсцис називають нулями або коренями функції.

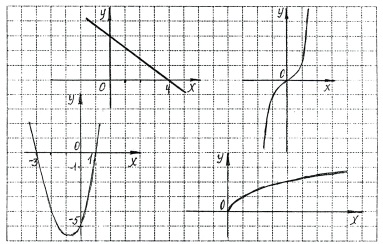
Вкажіть нулі функції на графіках.

Отже, значення аргументу, при яких значення функції дорівнює нулю, нази­вають нулями функції.

Вкажіть на цих малюнках (мал.1) проміжки, на. яких функція набуває додатних зна­чень, від'ємних, значень.

Відповідь.

а) (-∞, 4); (4; ∞).

б) (0; ∞); (-∞;0).

в) (0; ∞).

г) (-∞;3)U(1;∞); (-3; 1).

Проміжки на яких функція має однакові знаки, називають проміжками знакосталості. Для визначення проміжків знакосталості треба розв'язати нерівності f(х) > 0, f(х) < 0.

 

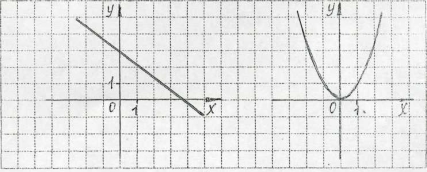
2. Охарактеризуйте зміну значення функції із зростанням аргументу.

Таким чином функцію називають зростаючою на деякому проміжку, якщо бі­льшому значенню аргументу з цього проміжку відповідає більше значення функ­ції.

Функцію називають спадною на деякому проміжку, якщо більшому значен­ню аргументу з цього проміжку відповідає менше значення функції.

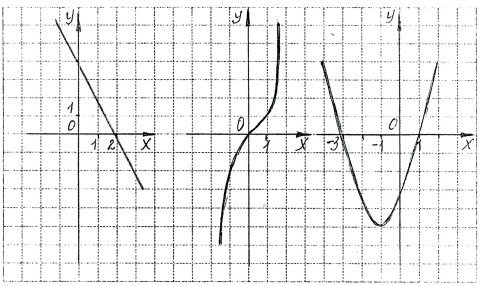
Вкажіть проміжки зростання й спадання функції.

 

Відповідь:   а) спадає на (-∞; ∞);

б) зростає на (-∞; ∞);

в) спадає на (-∞; -1); зростає на (-1; ∞).

Графічне задання функції наочно ілюструє проміжки її зростання й спа­дання.

Давайте визначимо чи є дана функція зростаючою (спадаючою), якщо во­на задана формулою у = f(х).

у = Зх - 3.

Нехай х₁ і х₂ - два довільні значення аргументу з області визначення, причо­му   х₂ >  х₁, а у₁ і у₂ відповідні їм значення функції, тобто

у₁ = 3х₁ - 3, у₂ = Зх₂ - 3.

Розглянемо різницю:

у ₂ – у₁ =(3 · х₂ - 3)- (3 · х₁ - 3)= 3· х₂ – 3 - 3 · х₁ + 3 = 3 · х₂ - 3.

Оскільки  х₂ >  х₁, то х₂ -  х₁ > 0.

Тоді 3 ·(х₂ - х₁) > 0; у₂ - у₁ >0, у₂ >у₁. Більшому значенню аргументу відповідає більше значення функції. Отже, дана функція зростаюча.

Зростання і спадання функцій яскраво відображено в українських прислів'ях. Адже прислів'я - це відображення стійких закономірностей, перевірених багатові­ковим досвідом народу,

1) Чим далі в ліс, тим більше дров.

2) Земля багата народ багатий.

3) З малої іскри великий вогонь буває.

4) Багато снігу - багато хліба.

5) Де багато крику, там мало роботи.

6) Хочеш більше знати, мусиш менше спати.

7) Хто високо літає, гой низько сідає.

8) Менше говори - більше почуєш.

 

3. Розглянемо функції f(х) = х² і g(х) = х³.

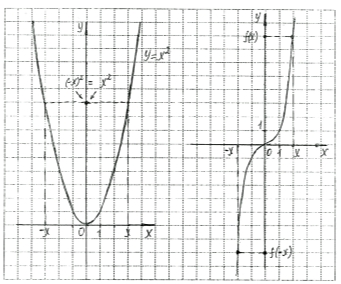
Демонструємо за допомогою мультимедійної системи табл.1 навчального посібника.

 

Область визначення цих функцій симетрична відносно початку координат. Для функції f(х) характерна властивість f(-х) = f(-х)² = х² = f(х), і графік її симетрич­ний відносно осі ординат, f(х) - функція з парним показником, тому її назвали парною.

Для функції g(х) характерна властивість g(-х) = (-х)³ = -х³ = -g(х), і графік її симетричний відносно початку координат. Це функція з непарним пока­зником, тому її назвали непарною.

Поняття парної і непарної функції поширимо на всі функції з областю ви­значення, симетричною відносно початку координат. Даємо означення парної й непарної функцій.

Функцію у = f(х) називають парною, якщо для будь-якого значення х з об­ласті її визначення значення - х також належить області визначення і виконується рівність f(-х) = f(х).

Функцію у = f(х) називають непарною, якщо для будь-якого значення х з області її визначення значення - х також належить області визначення і виконуєть­ся рівність f(-х) = -f(х).

Наводимо приклади дослідження функцій, на парність:

1) f(х) = х³ + х;

   D (f) = (-∞;∞) - симетрична відносно початку координат;

   F(х) = (-х³) - х = -х³ - х = - (х³ + х) = - f(х).

Функція f непарна і графік її симетричний відносно початку координат.

2) g(х) = х  - 4х²;

   D(g) = (-∞; ∞ ) - симетрична відносно початку координат;

   g(-х) = (-х) - 4(-х)² = х - 4х² = g(х).

Функція g парна і графік її симетричний відносно осі ординат.

3) φ(х) = х³ + 2х²;

   D(φ) = (-∞; ∞) - симетрична відносно початку координат;

   φ(-х) = (-х)³ + 2(-х)² = -х³ + 2х² ≠ ± φ(х).

Функція φ ні парна, ні непарна, її графік не симетричний ні відносно осі ординат, ні відносно початку координат.

 

Ш. Формування умінь і навичок.

1) Усне розв'язування вправи № 225.

На рисунку 34 зображено графік функції у = f(х).

Вкажіть:

а) область визначення і область значень функції;

б) нулі функції;

в) проміжки знакосталості;

г) проміжки, на яких функція зростає;

д) проміжки на яких функція спадає;

е) найбільше та найменше значення функції.

Розв’язання.

а) [-7; -16]; [-2; 4];

б) х = -3; х = 4; х = 8; х = 14,5.

в) (-7; -3); (-3; 4); (4; 8); (8; 14,5); (14,5; 16).

г) зростає на (7; 1) і (6; 12); спадає на (1; 6); (12; 16).

д) у = -2 – найменше значення функції.

   у = 4 – найбільше значення функції.

2) Колективне розв'язування вправи.

Побудуйте графік функції у = -. Користуючись графіком, вкажіть:

а) проміжки, на яких функція набуває додатних значень; від'ємних значень;

б) проміжки на яких функція зростає; спадає.
Чи є дана функція парною; непарною?

Розв 'язання.

 

х	-8	-4	-2	-1	1	2	4	8
у			1	2	-2	-1	-	-

а) у > 0 при х є (-∞; 0), у < 0 при х є (0; ∞);

6) зростає на (-∞; 0) і ( 0; ∞);

f(-х) = -()  = - (- ) = -f(х). Виконується умова, непарності.

Отже, у = - - непарна,

IV. Закріплення навичок та умінь. (Тестування).

Варіант 1.

1)

 

Функція у =f(х) задана графіком. Як називають:

1. Проміжок [-3; 6] осі х, який утворюють усі значення аргументу х?

а) областю визначення функції;

б) областю значень функції;

2. Проміжок [-4; 4] осі у, який утворюють усі значення змінної у?

а) областю визначення функції;

 б) областю значень функції.

3. Числа -2 і 5, за яких значення функції дорівнює 0?

 а) нулями  аргументу;

 б) нулями функції.

4. Проміжок [-3; 2] осі х, на якому за збільшення аргументу х  значення  функ­ції у збільшуються?

 а) проміжком зростання функції;

 б) проміжком спадання функції.

5. Проміжок [2; 6] осі х, на якому за збільшення аргументу х значення функції у зменшуються?

а) проміжком зростання функції;

б) проміжком спадання функції.

Яках значень набуває функція у = f(х):

6. На проміжку (-2;5)?

а) від'ємних;

б) додатних.

7. На проміжках (-3; -2) і (5; 6)?

а) від'ємних;

б) додатних.

 

Чому дорівнює:

б) -4.

а) 4;

б) 6.

10. Значення функції, якщо х = -1?

а) -2.5;

б) 2.

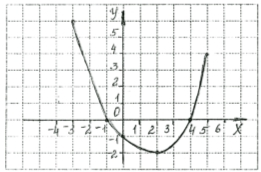
2)

Функцію у = f(х) задано графіком. Вказати:

1. Значення функції, якщо х = 3:
а) у = -1;

 б) у = 1.

 в) [-3; 5].

 в) у = 0;

 в) у =6.

 в) [0; 6].

 а) -3 і 5;

 б) -1 і 4;

в) 0.

9. Проміжок осі х, на якому функція зростає:

 а) [-3;2];

 б) [2; 5];

 в)[-3;4].

 б) [2; 5];

 в) [-3; 4].

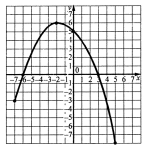3)

Функцію у = f(х) задано графіком. Вказати:

1) значення функції, якщо х = 3;

2) область визначення функції;

3) найменше значення функції;

4) найбільше значення функції;

5) область значень функції;

6) нулі функції;

7) проміжок осі х, на якому функція набуває додатних значень;

8) проміжок осі х, на якому функція набуває від'ємних значень;

9) проміжок осі х, на якому функція зростає;

10) проміжок осі х, на якому функція спадає.

 

Варіант 2.

1)

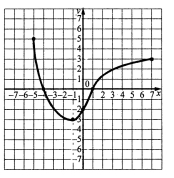
Функція у =f(х) задана графіком. Як називають:

1. проміжок [-5; 7] осі х, який утворюють усі значення аргументу х?

а) Областю значень функції;

б) Областю визначення функції.

2. проміжок [-3; 5]осі у, який утворюють усі значення змінної у?

а) Областю значень функції;

б) Областю визначення функції.

 б) Нулями функції.

4. Проміжок [-1; 7] осі х, на якому значення функції у збільшуються за збіль­шення аргументу х?

а) Проміжком зростання функції;

б) Проміжком спадання функції.

5. Проміжок |-5; -1] осі х, на якому значення функції у зменшуються за збільшення аргументу х?

а) Проміжком зростання функції;

б) Проміжком спадання функції.

Яких значень надуває функція у = f(х):

6. На проміжку (-4; 1)?

7. На проміжку [-5; -4) U (1; 7]?

 а) Від'ємних;

 б) Додатних.

Чому дорівнює:

8. Найменше значення функції/

 а) -1;

 б) -3.

9. Найбільше значення функції?

 а) 3;

 6) 5.

10. Значення функції, якщо х = -1?

 а) -3;

 б) -3,5.

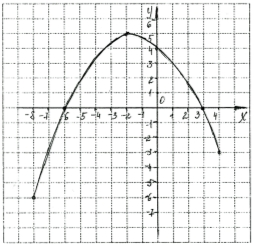
2)

Функцію у = f(х) задано графіком. Вказати:

1. Значення функції, якщо х = 1:

 а) у = 2,5;

 б) у = 3.

2. Область визначення функції:

 а) [-6; 3];

 б) [-6; 5];

 в) [-8; 4]

3. Найменше значення функції:

 а) у = -8;

 б) у = -6;

 в)у = -3.

4. Найбільше значення функції:

 а) у = 5;

 б) у = 4;

 в) у = 3.

5. Множину значень функції:

 а) [-6; 4];

 б) [-6; 5];

 в) [-8; 4].

6. Нулі функції:

 а) -6 і 3;

 б) 4;

 в) 0.

 б) (-8; -6) U (3; 4);

 в) (-6; 3).

 б) (-8;-6) U (3; 4);

 в) (-6; 3).

9. Проміжок осі х, на якому функція зростає:

 а) [-6;-2];

 б) [-8;-2|;

 в) [-2; 4].

10. Проміжок осі х, на якому функція спадає:

 а) [-2; 3];

 6) [-8; -2];

 в) [-2; 4].

 

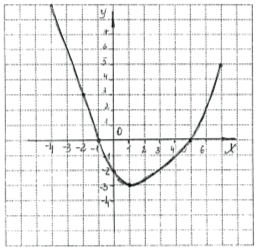
3)

Функцію у = f(х) задано графіком. Вказати:

1. Значення функції, якщо х = 3;

2. Область визначення функції;

3. Найменше значення функції;

4. Найбільше значення функції;

5. Множину значень функції;

6. Нулі функції;

7. Проміжок осі х, на якому функція набуває додатних значень;

8. Проміжок осі х, на якому функція набуває від’ємних значень:

9. Проміжок осі х, на якому функція зростає;

10. Проміжок осі х, на якому функція спадає.

 

V. Підсумок заняття.

Узагальнили та систематизували знання студентів про нулі, проміжки знакосталості, зростання й спадання функцій. Засвоїли поняття парності і непарності функцій та властивості графіків цих функцій.

VI. Домашнє завдання.

За підручником [1] §4,5

Вправа 1.

Знайдіть нулі функції.

а) у = х² + 2х – 8;

б) у = ;

в)

Вправа 2.

Побудуйте графік функції у = -2х – 2. Знайдіть її нулі. Вкажіть проміжки, на яких функція набуває додатних значень; від’ємних значень. Чи є дана функція зростаючою; спадно?

Вправа 3.

Парною чи непарною є функція:

а) у = 4х + х³;

б) у = х⁴ – 1;

в) у = х + 1.