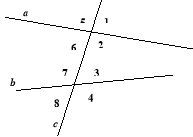
Урок "Властивості кутів, утворених перетином паралельних прямих січною".
План-конспект уроку засвоєння знань з геометрії у 7 класі з теми " Властивості кутів, утворених перетином паралельних прямих січною".
Мета уроку: - провести дослідження властивостей кутів, утворених перетином паралельних прямих січною;
- навчити учнів застосовувати їх для розв'язування задач та розпізнавати на малюнках;
- формувати зацікавленість у результатах спільної роботи;
- розвивати логічне мислення, математичне мовлення, інтерес до роботи з комп'ютерною технікою, інтерес до предмету та його історії.
Бердянська загальноосвітня школа І-ІІІ ступенів № 11
Бердянської міської ради Запорізької області
Властивості кутів, утворених перетином паралельних прямих січною.
(план - конспект уроку з геометрії у 7-му класі)
Підготувала
Іванова Юлія Анатоліївна
вчитель математики
перша категорія
м. Бердянськ.
Тема уроку: Властивості кутів, утворених перетином паралельних прямих січною.
Мета уроку:
- провести дослідження властивостей кутів, утворених перетином паралельних прямих січною;
- навчити учнів застосовувати їх для розв’язування задач та розпізнавати на малюнках;
- формувати зацікавленість у результатах спільної роботи;
- розвивати логічне мислення, математичне мовлення, інтерес до роботи з комп’ютерною технікою, інтерес до предмету та його історії.
Тип уроку: засвоєння знань, вироблення вмінь.
Обладнання: мультимедійна система, презентація до уроку, креслярські інструменти, таблиця «Ознаки паралельності прямих», картки з індивідуальними завданнями.
Хід уроку
І. Організаційний момент
Доброго ранку! Готові до уроку? Усміхніться, налаштуйтесь на роботу. Ми розпочинаємо урок геометрії, і керуючись словами Миколи Івановича Лобачевского, що «Все в природі повинно бути виміряне, все має бути пораховано» звертаюсь до вас із питанням: як ви впоралися розрахунками у домашньому завданні? Давайте перевіримо.
ІІ. Перевірка домашнього завдання.
![]() На сьогодні були задані номери 207, 210б, 217. Перевірте їх за зразком. (Слайд)
На сьогодні були задані номери 207, 210б, 217. Перевірте їх за зразком. (Слайд)
Які правила ви використовували для пояснення розв’язку задач? (Відповіді учнів).
Подивіться у свої зошити і навпроти кожної правильно виконаної задачі з поясненнями поставте по 4 бали, якщо ж пояснень не має, то по 2 бали.
ІІІ. Мотивація навчальної діяльності учнів. Формулювання мети і завдань уроку.
Подивіться на екран, на якому я хочу продемонструвати вам оптичні ілюзії. Зверніть увагу на горизонтальні лінії. (Слайд)
(На екрані 9 ілюзій), коментую:
№3 ілюзія Вундта, 1896 р.
№6 ілюзія Грегорі, 1979р.
№9 Герінга «віяло»
Що поєднує ці ілюзії? (лінії криві, не паралельні)
А на справді всі ці прямі паралельні. Наші очі можуть ввести нас в оману. Особливість геометрії - її наочність, але повністю довіряти рисунку не можна. Тому треба використовувати інші способи, щоб перевірити паралельність прямих. Сьогодні на уроці ми будемо використовувати властивості кутів, щоб з’ясовувати чи паралельні дані прямі.
Отже і тема уроку сьогодні «Властивості кутів, утворених перетином паралельних прямих січною», відкрийте зошити і запишіть її. Тема уроку вже записана у вас на аркушах, в яких ви будете працювати на уроці. Погляньте на них уважно. За кожен вид роботи треба виставляти відповідні бали, а в кінці уроку підрахувати середнє значення. Запишіть своє прізвище на аркуші. Порахуйте свою оцінку за домашні задачі і виставте у клітинку «ДЗ».
ІV. Актуалізація опорних знань.
Враховуючі план уроку (слайд: пригадай, застосуй, виміряй, застосуй, доведи!), перейдемо до повторення теоретичних знань. Пропоную два завдання: «Знайдіть пару» та гра «Вірю-не вірю».
1. «Знайдіть пару»: ми повинні повторити назви і розташування кутів при перетині прямих січною. Подивіться на слайд: до внутрішніх кутів треба дібрати пару і записати у відповідну клітинку.
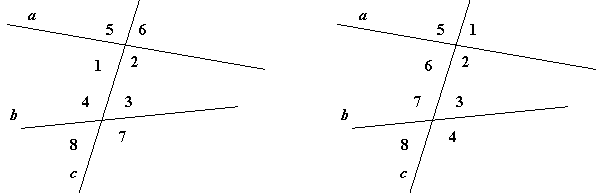
|
Робота біля дошки (1 учень-1 вид кутів) |
|
Самостійна робота. |
||||||||
|
Внутрішні Кути |
1 |
2 |
3 |
4 |
|
Внутрішні кути |
2 |
3 |
6 |
7 |
|
Внутрішній різносторонній |
3 |
4 |
1 |
2 |
Внутрішній різносторонній |
7 |
6 |
3 |
2 |
|
|
Внутрішній односторонній |
4 |
3 |
2 |
1 |
Внутрішній односторонній |
3 |
2 |
7 |
6 |
|
|
Відповідний |
8 |
7 |
6 |
5 |
Відповідний |
4 |
1 |
8 |
5 |
|
|
Вертикальний |
6 |
5 |
8 |
7 |
Вертикальний |
5 |
8 |
1 |
4 |
|
|
Суміжні |
2; 5 |
1; 6 |
4; 7 |
3; 8 |
Суміжні |
1; 6 |
4; 7 |
2; 5 |
3; 8 |
|
На самостійну роботу вам відводиться 3 хвилини. Починайте.
Час закінчився. Обміняйтеся в парах таблицями і проводимо взаємоперевірку - подивіться на екран, порахуйте правильні відповіді, і за кожну поставте 0,5 бала. Порахуйте оцінку і виставте у графу «С.р».
2. А зараз зіграємо у гру «Вірю-не вірю». Для відповідей перед кожним з вас на парті лежать два кольорових аркуша. Якщо ваша відповідь «так»- піднімайте зелений аркуш, якщо «ні»- то червоний.
За правильну відповідь виставляйте у графу «Вірю-не вірю» 1 бал.
Чи вірите ви, що…
1. Паралельні прямі на площині – це прямі, які перетинаються. (Ні)
2. Через точку, яка не належить прямій, можна провести лише одну паралельну їй пряму.(Так)
- Якщо у результаті перетину паралельних прямих січною утворилися
два кути по 80º. Можуть вони бути:
-
 відповідними (Так)
відповідними (Так)
- внутрішніми односторонніми (Ні)
- внутрішніми різносторонніми (Так)
- суміжними (Ні)
-
Прямі а і в будуть паралельними, якщо
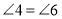 (Так)
(Так)
-
Прямі а і в будуть паралельними, якщо
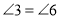 (Ні)
(Ні)
-
Прямі а і в будуть паралельними, якщо
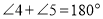 (Так)
(Так)
-
Прямі а і в будуть паралельними, якщо
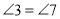 (Так)
(Так)
-
Прямі а і в будуть паралельними, якщо
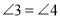 (Ні)
(Ні)
- Якщо один із внутрішніх кутів прямий, то інші теж прямі.(Так)
Порахуйте бали і виставте оцінку у графу Гра «Вірю - не вірю».
Виконавши попередні завдання ви показали готовність використовувати знання для розв’язання задач. Що саме вам допомагало визначати, що прямі паралельні? (Відповіді учнів, таблиця «Ознаки паралельних прямих»)
Можемо зробити висновок, що ознаки паралельності прямих дають змогу довести паралельність прямих або відшукати на рисунку паралельні прямі з множини пар прямих.
Тому мета нашого уроку - провести дослідження властивостей кутів, утворених при перетині паралельних прямих січною. Слайд «Цілі уроку».
V. Вивчення нового матеріалу.
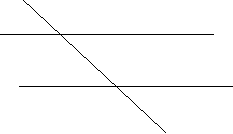
Для досягнення мети уроку ми повинні провести практичне, теоретичне і перевірочне дослідження. Відкрийте зошит і виконайте побудову.
Практичний дослід:
- Проведіть довільну пряму в
- Поставте точку А, яка б не належала прямій
- За допомогою косинця та лінійки побудуйте пряму а, паралельну в, і яка б проходила через точку А
- Проведіть січну с
- Позначте:
І. Внутрішні різносторонні кути цифрами 1 і 2
ІІ. Внутрішні односторонні кути цифрами 1 і 3
ІІІ. Відповідні кути цифрами 4 і 3
- Виміряйте їх величину за допомогою транспортира. (1 ряд- І, 2 ряд- ІІ, 3 ряд- ІІІ)
і запишіть результати вимірів у зошит
- Зробіть висновок
Час виконання – півтори хвилини. Дозволяється радитися, в межах пари, щоб сформувати спільну думку.
Приступайте до роботи.
Час вичерпано. Переходимо до формування спільної думки.
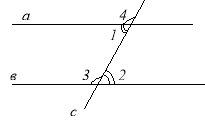 Слайд.
Слайд.
1 ряд. (Досліджували внутрішні різносторонні кути), що ви можете доповісти ?
Як позначаються рівні кути на малюнку?
Скільки пар рівних внутрішніх різносторонніх кутів ви бачите?
Позначте їх на своїх малюнках:пару тупих кутів-одною рисочкою, а пару гострих - двома рисочками
Перевірте правильність позначок, звірившись з дошкою.
Що ви можете повідомити про цю пару кутів? (![]() )
)
2 ряд (Досліджували внутрішні односторонні кути)
Якими цифрами позначаються внутрішні односторонні кути на малюнку?
Що ви можете повідомити про цю пару кутів? ![]()
Перевірте правильність позначок, звірившись з дошкою.
3 ряд. (Досліджували відповідні кути)
Позначте рисочками відповідні кути, до уже позначених внутрішніх кутів.
Перевірте правильність позначок, звірившись з дошкою
Що ви можете повідомити про цю пару кутів? (![]() )
)
Всі групи допишіть, будь-ласка, висновки досліду, у бланк відповідей:
Якщо ![]() , то
, то ![]() , або
, або
![]() , або
, або
![]() .
.
Теоретичний дослід.
(На слайді «Ознаки паралельності прямих»)
Якщо ![]() , або
, або
![]() , або
, або
![]() , то
, то ![]()
Твердження про кути є умовою, а твердження, що прямі паралельні – висновок.
Назвемо ці теореми прямими.
Ми сьогодні досліджуємо кути. Щоб твердження про кути було висновком, треба поміняти місцями умову і висновок.
Якщо в теоремі змінити розташування умови і висновку, отримаємо обернену теорему. Спробуємо. З яких слів починатиметься теорема?
Теоретичний дослід привів до висновку:
Якщо паралельні прямі перетинає січна, то внутрішні різносторонні і відповідні кути рівні, внутрішні односторонні в сумі становлять 180º.
Порівняйте отримані теореми з висновками практичної роботи. Що ви можете сказати?
Якщо ![]() , то
, то ![]() , або
, або
![]() , або
, або
![]() .
.
(Вони однакові).
Дослід перевірочний.

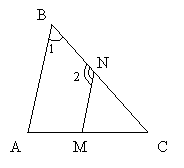
На дошці є малюнок на якому паралельні прямі перетинає січна і набори відповідних кутів.
Завдання для 2 ряду. Покажіть, що внутрішні різносторонні кути рівні.
Завдання для 3 ряду. Продемонструйте без допомоги транспортиру що відповідні кути рівні.
Завдання для 1 ряду. Покажіть, що внутрішні односторонні кути у сумі дорівнюють 180 градусів.
Ми провели дослідницьку роботу і можемо зробити висновок, що отримані практичні і теоретичні дані вірні.
Порадьтеся у парах на яку оцінку ви заслуговуєте і виставте її у графу «Дослідження»
Фізкультхвилинка для очей (слайд)
VІ. Розв’язання задач за готовими малюнками. Ваші очі відпочили, тож перейдемо до закріплення повторених знань і усно розв’яжемо задачі за готовими малюнками.

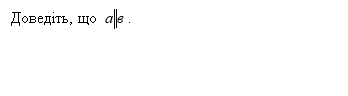
№1.
![]()
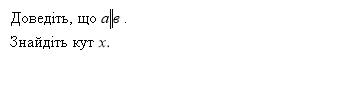 №2
№2

Перейдемо до письмового розв’язання задач. (В цей час декільком учням даю завдання на картках, які вони мають розв’язати за той час, що клас працює з учнями біля дошки).
До дошки одночасно визиваю 2 учнів, які розв’язують задачі…
№3 (8 балів)


№4. (10 балів)
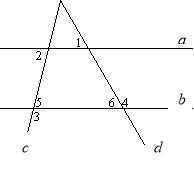
Збираю картки з індивідуальними завданнями.
VІІ. Домашнє завдання. Відкрийте щоденники і запишіть домашнє завдання: опрацювати п. 7 с. 55-56, розв’язати задачі с.69 № 6, № 7 (достатній рівень), № 10*(підвищений рівень).
У стовпчику таблиці «Оцінка» виставте свій бал за урок, порахувавши середнє арифметичне з попередніх стовпчиків.
Історичне повідомлення
Я попрошу … познайомити нас з однією історичною особистістю і її роботою.
Якщо повернутися в ΙΙΙ ст. до н. е. на територію сучасного Єгипту в місто Олександрію, ми потрапимо в Мусейон – науковий центр, де працювали запрошені з усього світу найвидатніші вчені з різних галузей наук.
Започаткував там свою школу і грецький математик Евклід.
Для своїх учнів він вирішив створити підручники, об’єднавши в них всі відомі на той час геометричні факти, установивши між ними логічні зв'язки, доповнивши своїми понад чотирма сотнями доведень і аксіом.
Вийшло 13 книг – сувоїв, які він назвав «Основи». У цієї праці дивна доля. Вона була настільки вдалою і відповідала потребам часу, що її слава затьмарила славу самого автора. Ні місця народження, ні фактів із життя Евкліда ніхто не запам'ятав, а ось «Основи» - були основним підручником з геометрії понад 2300 років. По ним вивчав геометрію весь світ.
Італієць – Галілей. Поляк – Копернік. Француз – Декарт. Росіянин – Ломоносов. Англієць – Ньютон і багато інших видатних вчених. Вчимо її і ми. Геометрія, яку вивчають в школі, є Евклідовою. Побудованою на аксіомах – реченнях, які приймаються на віру, не потребують доведення і які допомагають доводити інші твердження – теореми. Одна із таких аксіом носить ім'я свого творця - аксіома Евкліда.
Вона звучить так: « Через точку, яка не лежить на прямій , можна провести тільки одну пряму, паралельну даній»
Ця аксіома йшла до нас 23 сторіччя і повинна бути вивчена!

Хто уважно слухав, зможе мені відповісти:
- Хто створив перший підручник з геометрії? (Евклід)
- Як він називався? (Основи)
- Яке твердження називають аксіомою? (Яке не потребує доведення)
- Яке твердження називають теоремою? (Яке треба довести)
- Як звучить аксіома Евкліда? Давайте разом її прочитаємо
« Через точку, яка не лежить на прямій , можна провести тільки одну пряму, паралельну даній»
VІІІ. Підсумки уроку.
На початку уроку ми з вами поставили цілі (слайд) до яких повинні були дійти. На вашу думку, чи досягли ми своїх цілей? Що вам сподобалось на уроці? А що ні?
У стовпчику таблиці «Оцінка» виставте свій бал за урок, порахувавши середнє арифметичне з попередніх стовпчиків.
Я теж вважаю, що мети ми досягли, властивості кутів утворених при перетині паралельних прямих січною засвоїли, а далі ми вирушимо на наступному уроці.
Урок закінчився. Дякую усім.
Додаток А
 Картка №1 c
Картка №1 c
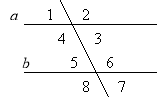
![]()
![]() a 1 2
a 1 2
Чи паралельні прямі a і b? 4 3
Знайдіть всі інші кути. b 5 6
8 7
Картка №2
Прямі ![]() , c- січна,
, c- січна, ![]() . Знайдіть всі інші кути.
. Знайдіть всі інші кути.


![]()
![]()
![]() 1 2 5 6
1 2 5 6
![]() 4 3 8 7
4 3 8 7
Картка № 3
Чи паралельні прямі m і n?
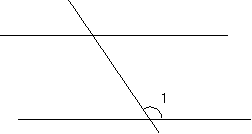 m 1280
m 1280
n
520
 Картка №4
Картка №4
Додаток Б
Відповіді
Картка №1
![]() - суміжні кути.
- суміжні кути.
![]()
![]() - відповідні кути при перетині прямих a и b січній с. Отже, прямі a і b паралельні.
- відповідні кути при перетині прямих a и b січній с. Отже, прямі a і b паралельні.
![]() - вертикальні кути.
- вертикальні кути.
![]() - вертикальні кути.
- вертикальні кути.
![]() - внутрішні різносторонні кути
- внутрішні різносторонні кути
![]() - внутрішні різносторонні кути.
- внутрішні різносторонні кути.
![]() - відповідні кути.
- відповідні кути.
Відповідь: ![]() ,
,![]() .
.
Картка №2
![]() - внутрішні односторонні кути
- внутрішні односторонні кути
Якщо дві паралельні прямі перетинає січна, то сума внутрішніх односторонніх кутів 1800. ![]() ,
,
![]() - внутрішні різносторонні кути.
- внутрішні різносторонні кути.
![]() - вертикальні кути,
- вертикальні кути,
![]() - вертикальні кути,
- вертикальні кути,
![]() - відповідні кути,
- відповідні кути,
![]() - відповідні кути,
- відповідні кути,
![]() - вертикальні кути,
- вертикальні кути,
![]() - вертикальні кути,
- вертикальні кути,
Відповідь: ![]() ,
, ![]() .
.
Картка №3
![]() -суміжні кути. Кути 1280 і
-суміжні кути. Кути 1280 і ![]() відповідні кути. Якщо дві прямі перетнуті січною і відповідні кути рівні, то прямі паралельні.
відповідні кути. Якщо дві прямі перетнуті січною і відповідні кути рівні, то прямі паралельні.
Отже, m II n
Картка№4
![]() ,
, ![]() (властивість кутів рівнобедреного трикутника)
(властивість кутів рівнобедреного трикутника)
а![]() (за умовою), то
(за умовою), то ![]() - внутрішні різносторонні, тому
- внутрішні різносторонні, тому ![]() за ознакою паралельності прямих.
за ознакою паралельності прямих.
Двадцять сьоме листопада
Класна робота
Тема: Властивості кутів, утворених перетином паралельних прямих січною.
№1 Домашнє завдання
|
№207 |
№210 (б) |
№217 |
Оцінка |
|
|
|
|
|
№2 Самостійна робота «Знайдіть пару»
|
|
||||
|
Внутрішні кути |
2 |
3 |
6 |
7 |
|
Внутрішній різносторонній |
|
|
|
|
|
Внутрішній односторонній |
|
|
|
|
|
Відповідний |
|
|
|
|
|
Вертикальний |
|
|
|
|
|
Суміжні |
|
|
|
|
|
Оцінка |
|
Кількість правильних відповідей помножити на 0,5.
№3 Гра «Вірю - не вірю» За правильну відповідь - по 1 балу.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Оцінка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
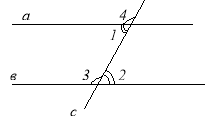 №4. Дослідження
№4. Дослідження

№5 Розв’язання задач
Задача 3.

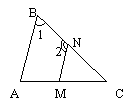
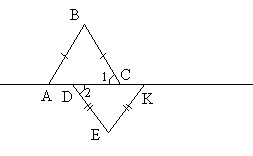
 Задача 4.
Задача 4.
|
Вид роботи |
Дом.зав |
Сам.роб |
Вірю-не вірю |
Дослідження |
Оцінка |
Дод. бали |
Підсумкова оцінка |
|
Бали |
|
|
|
|
|
|
|



про публікацію авторської розробки
Додати розробку