Урок з алгебри для 9 класу на тему "Частота та ймовірність випадкової події".

Урок № 51                                                                                          Дата    29.04.2020р.

Добрий день, дорогі мої учні!

Марк Ива́нович Башмако́в — советский математик, педагог, автор многочисленных учебников и пособий для школьников, доктор физико-математических наук, профессор, действительный член Российской академии образования однажды сказал:

“Главная сила математики состоит в том,

что вместе с решением одной конкретной задачи

 она создаёт общие приёмы и способы,

применимые во многих ситуациях,

которые даже не всегда можно предвидеть”.

         Відкрийте зошит і записуйте:

Двадцять дев´яте  квітня

Класна робота

Тема. Частота та ймовірність випадкової події.

Мета уроку: домогтися засвоєння учнями змісту понять: випадкова подія, вірогідна подія, неможлива подія; означення ймовірності випадкової події; навчитися визначати за формулою ймовірність простої події, а також розв’язувати задачі, що передбачають обчислення ймовірності за формулою. Розвивати цікавість до математики, уяву, увагу, логічне мислення, а також культуру математичної мови через математично грамотні висловлювання. Виховувати відповідальність, працелюбність, взаємодопомогу, культуру математичних записів та інтерес до вивчення предмета.

Тип уроку: засвоєння нових знань і вмінь.

Хід уроку

І. Організаційний етап

Сьогодні ми з вами продовжуємо вивчати нову тему “Основи комбінаторики, теорії ймовірностей та статистики”, а саме – Частота та ймовірність випадкової події. Тому приготуйте необхідні зошит, підручник і  до роботи…

II. Актуалізація опорних знань та вмінь учнів

А щоб вивчити щось нове необхідно пригадати пройдений матеріал.

1.                   Що в математиці називають дробом? (Дріб — у математиці це представлення чисел або математичних величин у вигляді результату операції ділення.)
2.                   Де застосовують дроби? (Дроби застосовують для позначення частин деяких об'єктів: демографія, біологія, хімія…)
3.                   У якій формі зазвичай записують дроби?
4.                   Як записують звичайний дріб?
5.                   Що називають чисельником?
6.                   Що називають знаменником?
7.                   Що називають відсотком?
8.                   Як перевести звичайні дроби у відсотки?
9.                   Перевести у відсотки дроби : ½; ¼ ;  ¾; 1/3; 8/25 = (8 ∙ 100% : : 25 = 32).
10.              Із послідовності чисел 9; 7; 6; 2; 3; 5; 20 вибрати парні (чётные – рус.), непарні (нечётные – рус.), дільники числа 4?

ІІІ. Викладення нового матеріалу

Чи можна якимось чином оцінити шанс появи результату, який нас цікавить? Відповідь на це питання дає розділ математики, що називається теорія ймовірностей.  

Теорія ймовірностей – це математична наука, що вивчає закономірності випадкових процесів і подій.

Корисність одержуваних знань полягає як у тому значенні, яке мають ці знання для розуміння і пізнання закономірностей оточуючого нас світу, так і можливості їх безпосереднього застосування при вивченні інших наук і в повсякденному життєвій практиці.

 Зародження теорій ймовірностей відбулося у пошуках відповіді на питання: як часто відбувається та чи інша подія в серії випробувань?

Як зародилася наука теорія ймовірностей? Хто з видатних вчених присвятив свої праці саме ймовірності?

Що називають випробуванням? Експериментом? Подією?

Під експериментом (випробуванням) розуміють деяку сукупність умов, в яких спостерігається те або інше явище, фіксується той або інший результат.

Слово “подія” в побуті застосовують до значних явищ (день народження, іспит, весілля), а в математиці – до всіх можливих наслідків ситуації, що розглядається наприклад при киданні гральної кістки подія-це випадання тієї або іншої грані.

 Подією називається усякий факт, який в результаті експерименту може відбутися або не відбутися.

Події будемо позначати великими літерами латинським А, В, С. Вони бувають:

• Події, які за даних умов обов’язково відбуваються, називають достовірними (зміна дня і ночі).
• Події, які за даних умов не можуть відбутися, називають неможливими.
• Події, які за даних умов іноді відбуваються, а іноді не відбуваються, називаються можливими або випадковими.
• Події, можливості настання яких однакові називаються рівноможливими або рівноімовірними (підкидання монети).

Наведемо приклади подій.

• черепаха навчитися говорить;
• вода в чайнику, що стоїть на гарячій плиті закипить;
• ви виграєте беручи участь у лотереї;
• ви програєте партію в шахи;
• на наступному тижні може зіпсуватися погода;
• ви натиснули на дзвінок, а він не задзвонив;
• після четверга буде п’ятниця;

• влітку у школярів будуть канікули;
• взимку випадає сніг;
• при включенні світла, лампочка перегорить
Об’єднайте події у групи. За якими ознаками ви це зробили? Узагальніть визначення.

Ймовірністю події називається чисельна міра ступеня об'єктивної можливості появи події в результаті нового експерименту.

Чому буде дорівнювати імовірність події:

• черепаха навчитися говорить
• вода в чайнику, що стоїть на гарячій плиті закипить
• ви виграєте беручи участь у лотереї
Властивості ймовірності будь-якої події:

0 ≤ P(A) ≤ 1

 Якщо A – вірогідна подія, то P(A)=1
Якщо A – неможлива подія, то P(A)=0
Якщо A – випадкова подія, то 0≤ P(A) ≤ 1

Ймовірність події А як можливого виходу деякого експерименту визначається відношенням кількості випадків, що сприятливі для події А, до загальної кількості випадків у даному експерименті. Таким чином, якщо m – кількість випадків, що сприятливі для події А, а n – загальна кількість випадків у даному експерименті, то ймовірність події А випадковів події :   

 ІV. Формування вмінь і навичок учнів

Приклад 1. Знайдiть iмовiрнiсть того, що в результатi пiдкидання грального кубика випаде парне число очок.

Розв’язання:

Ймовірність  події А обчислюється за формулою: Р(А)=m/n. Дана подія може відбутися трьома способами: випало 6 очок, випало 4 очка, випало 2 очка. Отже m=3. Всього можливо шість подій під час даного експерименту, тому  n=6. Тоді Р(А)=3/6=1/2=0,5=50%.

Відповідь : ½ або 50%

Алгоритм для розв’язання задач за допомогою класичного визначення:

1. позначити подію
2. підрахувати кількість загальних випадків у даному експерименті
3. підрахувати кількість випадків, сприятливих для даної події
4. знайти відношення сприятливих наслідків до числа усіх наслідків

Приклад 2. В урнi мiститься 10 однакових за розмiром кульок: 6 жовтих i 4 си­нiх. Кульки перемiшали. Знайдiть iмовiрнiсть того, що навмання вибрана кулька буде:

1. синього кольору;         
2. жовтого кольору;
3. чорного кольору;
4. будь-якого кольору.

Розв’язання:

Подія А може відбутися чотирьма способами, подія В-шістьма, подіяС-неможлива подія, подія D така, що завжди відбудеться. Одну кульку можна витягнути десятьма способами. Тому Р(А)=4/10=2/5=0,4=40%,

                               Р(В)=6/10=3/5=0,6=60%,  

                               Р(С)=0,     

                               Р(D)=1=100%.

Приклад 3: У лотереї 100 квитків, з них 5 виграшних. Яка ймовірність програшу?

Чим дана умова відрізняється від попередніх? Чи можемо ми одразу обчислити імовірність? Чому?

Розв’язання:

А – програти: результатів – 100; Шанс = 100-5 = 95, тоді Р (А) =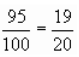
 

Приклад 4.

З натуральних чисел від 1 до 24 учень навмання називає одне. Яка імовірність того, що це число є дільником числа 24?

Розв’язання:

Дільники числа 24: 1,2,3,4,6,8,12,24 =8

Р(А)=8/24=1/333%

V. Підведення підсумків уроку

1. Наведіть приклад:

1) випадкової події;     2) неможливої події;    3) вірогідної події.

2. Чи може ймовірність деякої події А дорівнювати:  0;         -1;       1;      0,25;    1,5?
3. У прогнозі погоди було сказано: наступного дня ймовірність опадів дорівнює 0,75. Що це означає?

Сьогодні ми з вами навчилися розв’язувати задачі на знаходження ймовірності, ознайомилися з новими поняттями. У житті часто доводиться  діяти так, щоб шанси на успіх були якнайбільшими, випадкову подію не можна передбачити, але можна знайти її імовірність. Мені б хотілося щоб ви реально оцінювали свої шанси і можливості. Дякую за урок!

Від класної роботи пропустили чотири клітинки вниз і записуємо:

Двадцять дев´яте квітня

Домашня  робота

VI.  Домашнє завдання

• Дослід: підкинути монету 20 разів і підрахувати скільки разів випав орел. Обчислити імовірність за формулою.

• Розв’язати задачі:

1.  У шухляді письмового столу лежать 12 олівців однакової форми і розмірів, з яких 4 олівці - кольорові, а інші - прості. Яка ймовірність того, що, відкривши шухляду, навмання взятий олівець буде простий?

2.  З 40 стандартних і 4 нестандартних деталей для контролю взято навмання вісім, які виявилися стандартними. Знайти ймовірність того, що наступна взята навмання деталь буде стандартною.

• Творче завдання: скласти міні-проект «Імовірність випадкової події у моєму житті»

На Google–диск відправите: відповіді зі розділу “Підведення підсумків уроку” та домашню роботу!