Урок з алгебри для учнів 10 класу на тему "Тригонометричні функції, їх графіки та властивості"

УРОК НА ТЕМУ: «ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ ЇХ ГРАФІКИ І ВЛАСТИВОСТІ»

Бокало Г.В., викладач математики ВПУ №29 м.Львова

Тема уроку: Тригонометричні функції їх графіки і властивості.

Мета уроку:

         Навчальна: Узагальнення й систематизація знань і вмінь учнів з вивченої              теми; удосконалення вмінь із використанням  властивостей тригонометричних функцій проводити порівняння значень функцій, будувати графіки, визначати період тригонометричних функцій, парність і непарність, досліджувати функції на монотонність.

      Розвиваюча:Вдосконалити навички побудови графіків тригонометричних          функцій; розвивати просторову уяву учнів ,побудови графіків тригонометричних функцій при різних значеннях кутів.

         Виховна:Виховувати в учнів точність, акуратність, при побудові графіків тригонометричних функцій, стимулювати пізнавальну активність учнів.

Тип уроку: узагальнення й систематизація знань і вмінь учнів.

Методи навчання: словесний і наочний .

Обладнання урок: мультимедійні  засоби навчання, індивідуальні карточки з задачами,

Між предметні зв’язки: Фізика “Гармонічні коливання”, “Змінний струм”

                                            Всесвітня історія “ Культура XVII-XIIXст.”

Література: Г.П.Бевз, В.Г. Бевз Математика 10. Підручник для загальноосвітніх навчальних закладів. Рівень стандарту.

Л.В. Колеснікова ,Г.Й. Коротіна  Алгебра і початки аналізу 10 кл. Плани-конспекти уроків.

Т.Л.Корнієнко, В.І.Фіготіна Тиждень математики в школі 5-11 класи. Видавництво

“Ранок” 2008.

Хід уроку

I. Організація    навчальної   діяльності .                                      

Перевірка учнів   

Напередодні уроку учні, щоб об’єднатися в групи , тягнуть зі скриньки  картки певних кольорів (наприклад , рожевого, білого, червоного, синього ).

      На початку уроку групи розсідаються згідно з кольорами   ( футболки  відповідних кольорів ) й функцією.

  Рожевий- функція y=sinx.

  Білий- y=cosx.

  Червоний- y=tgx.

  Синій- y=ctgx

II. Мотивазація навчальної діяльності.

Оголошення теми і мети уроку.Представлення керуючих підгруп і повідомлення завдань.

III. Узагальнення і систематизація знань учнів.

 Заслуховується звіт кожної підгрупи  про  властивості й графік  відповідної функції. Після звіту кожної  підгрупи члени іншої підгрупи  в разі необхідності роблять доповнення до відповідей і виправляють помилки. Тоді кожна підгрупа доповнює свої відповіді історичними відомостями.

Властивості  функції :

1.               D(sin x) = R
2.               E(sin x) = [- 1 ; 1]
3.               y = sin x – непарна функція,

 графік симетричний відносно початку

 координат

4. періодичність:  T = 2π

5. sin x  = O при х = πn, nZ (нулі функції)

6.  проміжки знакосталості:

 sin x > 0  при       0 + 2πn < x < π+ 2πn, nZ

 sin x < 0  при       π + 2πn < x < 2π+ 2πn, nZ

7. проміжки монотонності:

 x [- ^π /₂  + 2πn; ^π /₂ + 2πn], nZ – зростає

 x [ ^π /₂  + 2πn;  ^3π /₂ + 2πn], nZ– спадає

8. екстремуми:

 y _max = 1    при х = ^π /₂  + 2πn, nZ

 y _min = - 1    при х = - ^π /₂  + 2πn, nZ

Властивості  функції :

1.               D(cos x) = R
2.               E(cos x) = [- 1 ; 1]
3.               y = cos x –парна функція,

 графік симетричний відносно

 осі ординат

4. періодичність:  T = 2π

5. cos x  = 0 при х = ^π /₂ + πn, nZ (нулі функції)

6. проміжки знакосталості

 cos x > 0 при  - ^π /₂ + 2πn < x <  ^π /₂ + 2πn, nZ

 cos x < 0 при    ^π /₂ + 2πn < x < ^3π /₂ + 2πn, nZ

7. проміжки монотонності:

 x [ π+ 2πn; 2π+ 2πn], nZ –зростає

 x [0 + 2πn;  π+ 2πn], nZ– спадає

8. екстремуми:

 y _max = 1      при х = 2πn, nZ

 y _min = - 1    при х = π+ 2πn, nZ

Властивості  функції :

1.               D(tg x) =   x R/ ^π /₂ + πn, nZ    
2.               E(tg x) = R
3.               y = tg x – непарна функція

 графік симетричний відносно початку

 координат

4. періодичніть:  T = π

5. tg x  = 0 при х = πn, nZ (нулі функції)

6. проміжки знакосталості:

 tg x > 0 при     0 + πn < x <  ^π /₂ + πn, nZ

 tg x < 0 при   - ^π /₂ + πn < x < 0 + πn, nZ

7. проміжки монотонності:

 x [- ^π /₂ + πn;  ^π /₂ + πn], nZ –зростає

8.  эестремумів немає

Властивості  функції :

1.               D(ctg x) =    x R / πn, nZ
2.               E(ctg x) = R
3.               y = ctg x –непарна  функція

 графік симетричний відносно початку

 координат

4. періодичність:  T = π

5. ctg x  = 0 при х = ^π /₂ + πn, nZ (нулі функції)

6. проміжки знакосталості:

 ctg x > 0 при     0 + πn < x <  ^π /₂ + πn, nZ

 ctg x < 0 при   ^π /₂ + πn < x < π + πn, nZ

7. проміжки монотонності:

 x [0+ πn; π+ πn], nZ – спадає

8.  екстремумів немає

 Тепер ми не можемо не згадати хто перший побудував графік функції синус, довів періодичність, Хто перший ввів позначення sinі cos.

1. Перший графік функції синус побудував Д. Валліс для двох обертів, зауваживши, що таких обертів може бути багато.

Джон Валліс

2. Перші графіки функцій косинус і тангенс для кутів першої чверті будував англійський математик І. Баррау (1630-1677), учитель І. Нютона.

Ісаак Баррау

3. Про періодичність синуса і косинуса знав Ф. Вієт.

Франсуа Вієт

4. Для розвитку тригонометрії багато зробив Л. Ейлер (1707-1783). До нього під синусом, косинусом розуміли не абстрактні числа, а довжини відрізків і пов'язували їх тільки з трикутниками та колом.

5. Ейле перший ввів позначення sinі cos розуміючи під ними відношення довжин відповідних відрізків, розглядав їх при довільних значеннях кута . Він перший вивів усі формули зведення.

Математична пауза . Вірш  про косинус.

Косинус мій, чому ти не синус?

Я б за знак функції винесла мінус

Чому ти не тангенс,що швидко зростає,

До нескінченності з прірви сягає?

Косинус, графік я твій намалюю,

В кольори різні його розфарбую,

В класі його почеплю на стіні-

Іншим на смуток, на втіху мені.

Ряд коливань, наче хвилі на морі...

Учням не суть вони розпач і горе.

Точок китичних там дуже багато,

Важко їх навіть усі пригадати.

То він зростає, а то він спадає,

Модуля більш одиниці не має.

Має проте він багато нулів,

Всіх їх назнавати не вистачить слів.

Після цього кожна підгрупа одержує й виконує  завдання практичного характеру.

       Групі “рожевих” : побудувати графік y=sin2x і вказати проміжки зростання й спадання цієї функції.

Розв'язування:

.

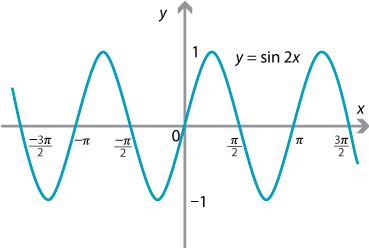
Функція зростає, якщо , де . Функція спадає, якщо ,.

       Групі “білих” : порівняти cosі cos.

Розв'язування:

Оскільки - кут першої чверті, то cos> 0.  - кут другої чверті, тобто cos < 0. Отже cos >  cos.

       Групі  “червоних”: дослідити  на  парність функцію f(x)=3x-tgx. 

Розв'язування:

- симетрична відносно початку координат.

.

Висновок: дана функція є непарна.

Групі “синіх”: побудувати графіки функції y=ctg2x і указати проміжки знакосталості цієї функції.

Розв'язування:

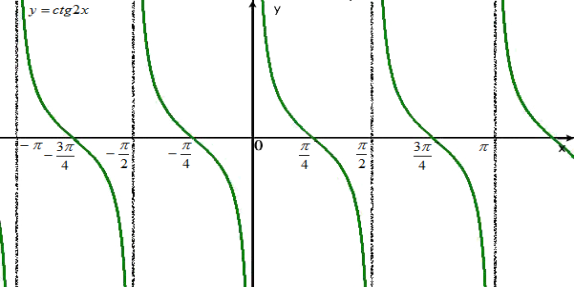
, якщо , де .

, якщо , де .

Цікаві питання які стосуються тригонометричних функцій.

 Перші  підгрупі:

1.   Як перекласти з грецької мови слово “тригонометрія”?

(Вимірюівання трикутників).

2.   Слово “тригонометрія” пропонували замінити на “гоніометрія” (вимірювання кутів). Чому?

 (Сучасна тригонометрія має справу з вимірюванням не трикутників, а кутів).

3.   У давнину час визначали за сонячним годиником. Вивчаючи залежність довжини тіні жердини  від кута нахилу  сонячних променів до земної поверхні, математики дійшли  до введення двох нових тригонометричних функцій. Яких саме? (Тангенс і котангенс)

Другі підгрупі:

1. Як з латинської  мови перекласти слова “синус”,  “косинус”, “тангенс”?       

(Згин, кривизна; доповнення синуса; дотичний).               

2. Яке слово в перекладі з латинської мови означає:

      а) “діяльність, виконання”,      (функція)

      б) “крок, ступінь”,     (градус)

      в) “промінь”.      (радіан (радіус)) 

3. Кутом якої чверті є ?   

( не належить ні до якої чверті)

Треті підгрупі:

 1. Чи завжди sin?  

 (якщо , то  )

      2. Який знак має добуток усіх основних тригонометричних функцій тупого

          кута?

 (мінус)

      3. Графік якої основної тригонометричної функції не перетинає вісь ординат?

 ()

Четверті підгрупі:

      1. Якщо болять зуби, ми звертаємось до стоматолога, якщо болить серце до

          кардіолога . А до якого лікаря треба звернутися, якщо болить синус?

 (До отоларинголога (вухо-горло-ніс). У носовій порожнині людини є  западинки - синуси, їх запалення називається синуситом.

 Другий варіант відповіді: у головному мозку теж є западинки - синуси).

      2. Наведіть приклад функції, яка і парна, і непарна; не зростаюча і не спад- 

          на; періодична, хоча і не має найменшого додатного періоду.

 (y=0)

3. Рятуючись від 40 розбійників, графік функції y=cosx відбіг управо на 4.

У графік якої функції він перетвориться?

()

IV. Підведення підсумків уроку та оцінювання знань учнів:

відповіді на запитання учнів;

оцінювання знань учнів та їх обгрунтування.

V. Домашнє завдання.

            Г.П.Бевз, В.Г.Бевз Математика: 10: підручник для загальноосвітніх навч. закл.: рівень стандарту. Повторити   14 ,15 cт. 109-114, ст. 117-125. Розв’язати№530, 532,541, 585в) г).