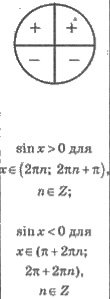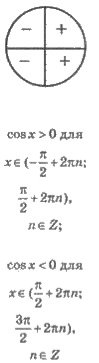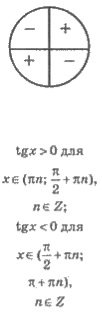Бліц−опитування на тему: «Властивості та графіки тригонометричних функцій».

Бліц−опитування на тему: «Властивості та графіки тригонометричних функцій».

Урок № 101.

Тема уроку: Властивості та графіки тригонометричних функцій.

Мета:

-узагальнити, систематизувати, поглибити знання та вміння учнів з теми «Властивості та   графіки тригонометричних функцій», формувати навички творчого застосування  знань під час розв’язування завдань високого рівня;

-розвивати логічне мислення, комунікативні здібності учнів;

- виховувати інтерес до математики, увагу, самостійність, формувати вміння працювати.

Тип уроку:узагальнення та систематизація.

Структура уроку

I Організаційний етап.

II. Актуалізація опорних знань учнів та мотивація навчальної діяльності.

III. Повідомлення теми та мети уроку.

IV.Застосування знань , вмінь і навичок.

V.Підведення  підсумків уроку та оголошення домашнього завдання.

Хід уроку

II. Актуалізація опорних знань учнів та мотивація навчальної діяльності.

« Бліц-опитування» .

Повторити властивості тригонометричних функцій за таблицєю ( таблиці лежать на партах)

Властивості тригонометричних функцій 

1. Знайти область значень функції:

1)у = 1/2cosx; 2)y = sinx+1; 3) у = соs²x+1; 4)у = 1/2tg²x+l; 5)y = sin2x.

Розв'язання. 1) Оскільки cos x змінюється від -1 до 1, то областю зміни функції у = 1/2cosx є відрізок [-1/2;1/2].

2) У виразі sinx +1 найменше значення першого доданка -1, а найбільше 1. Тому найменшим значенням виразу sinx+1 є число 0, а найбільшим — число 2. Отже, областю значень функціїу = sinx + 1 є відрізок [0;2].

3) У виразі cos²х+1 перший доданок змінюється від 0 до 1, а весь вираз — від 1 до 2. Отже, областю значень функції у=соs²х+1 є відрізок [1;2].

4) Перший доданок виразу 1/2tg² x+1 змінюється від 0 до +∞, оскільки tgx змінюється від -∞ до +∞, a tg²x — число невід'ємне. Тому областю значень функції у =1/2tg²x+1 є множина [1: +∞].

5) При будь-яких дійсних значеннях x областю значень функції у = sin 2х є множина [-1; 1].

2. Яке число більше:

1) sinπ/9 чи sinπ/4;         3) tgπ/4 чи tg3π/4;

2) cosπ/9 чи cosπ/4;         4)ctg(-π/8) чи ctg(-π/6)            

Розв'язання. 1) Числам a₁ = π/9 і a₂ = π/4 відповідають точки одиничного кола Р_a1 і Р_a2, які належать І чверті, де синус зростає. Оскільки π/4 >π/9, тo sinπ/4  > sinπ/9.

2) Косинус у І чверті спадає, тому cosπ/4 < cos π/9.

3) Числу a₁ = π/4 відповідає точка Р_a1 яка належить І чверті, а числу a₂ = 3π/4точка Р_a2, яка належить II чверті. Оскільки тангенс у І чверті додатний, а у II від'ємний, то tgπ/4>tg3π/4.

4).Числам -π/8 і -π/6 відповідають точки Р_a1 і Р_a2, які належать IV чверті, тобто проміжку (-π/2;0). Оскільки котангенс — функція спадна на кожному з проміжків області визначення, а -π/8>-π/6, то ctg(-π/8)<ctg(-π/6).

3. У яких чвертях може закінчуватися кут a, якщо:

l)|sin(-a)| = -sina;        2)|cosa| = -cosa;

3) |tga| = tga;              4) |ctg(-a)| = -ctga.

Розв'язання. 1) Оскільки синус — не парна функція, то дану рівність можна записати у вигляді |-sina| =-sina. Модуль будь-якого числа — число невід'ємне, тому невід'ємним має бути вираз — sina. Це означає, що sin a Є 0. Тому кут a може закінчуватися у III або у IV чверті.

2) За означенням модуля числа, модуль від'ємного числа дорівнює протилежному числу. Тому cosa за умовою набуває лише від'ємних значень. Це означає, що кут a може закінчуватися у II або у III чверті.

3) За означенням модуля tga — число невід'ємне. Тому кут a може закінчуватися або у І, або у III чверті.

4) Оскільки ctg(-a) = -ctga, то згідно з означенням модуля — ctga має бути числом невід'ємним. Тому кут a може закінчуватися у II або у IV чверті.

Самостійна робота з теми: «Основі співвідношення між тригонометричними  функціями одного аргументу».

        Дана самостійна робота проводиться 10-15 хвилин. Учні отримують завдання на карточках, відповідно до свого рівня знань виконують завдання такого ж  рівня, лише після виконання обовꞌязкових завдань можуть по бажанню виконати завдання іншого рівня.

         Відповідно виконавши завданя середнього рівня учень може отримати максимум 6 балів ( по 2 бали за кожне завдання), достатнього рівня – 9 балів     ( по 3 бали за кожне завдання), високого рівня − 12 балів (по 4 бали за кожне завдання).

ф