Урок з алгебри і початків аналізу для 10 класу (ПРОФІЛЬНИЙ РІВЕНЬ) на тему "Алгебраїчні рівняння вищих степенів"

Урок алгебри в 10 класі з використанням опорних схем та опорних карток  як засобу формування самоосвітньої та інформаційної компетентності

Тема: Алгебраїчні рівняння

Мета: Систематизувати знання учнів з теми «Розв’язування рівнянь», повторити теорію розв'язання рівнянь, виробити вміння визначати вид рівняння та вибирати найбільш раціональні способи розв’язування  даного рівняння.

Створювати умови для розвитку аналітичного мислення, вміння класифікувати факти.

Виховувати потреби в знаннях, культуру спілкування.

Обладнання уроку: дошка, таблиця для опорної схеми, опорні картки з д/з, портрети вчених, картки з індивідуальними завданнями.

Тип уроку: Урок узагальнення і систематизації знань.

 

Епіграф до уроку:

Більшість життєвих завдань вирішуються

як  алгебраїчні рівняння: приведенням їх до найпростішого вигляду.

                                   Л.М.Толстой.

Хід уроку

 

І. Перевірка домашнього завдання.

Розв’язки попередньо записані на дошці і учням пропонується провести взаємоперевірку в парах та поставити 1додатковий бал за правильну відповідь.

№1. Знайти кратність кореня х = – 2 для многочлена

f(x) = х⁷ + 5х⁶ + 6х⁵ – 3х⁴1 – 4х³ – 16х – 16.

Оскільки з умови зрозуміло, що х = – 2 – корінь, то використовуємо схему Горнера до тих пір поки R = 0.

	1	5	6	– 3	– 4	0	–16	–16
– 2	1	3	0	– 3	2	– 4	– 8	0
– 2	1	1	– 2	1	0	– 4	0
– 2	1	– 1	0	1	– 2	0
– 2	1	– 3	6	–11	20

 

Відповідь: х = 2 є коренем кратності 3, тобто f(x) = х⁷ + 5х⁶ + 6х⁵ – 3х⁴1 – 4х³ – 16х – 16 = (х + 2)³(х⁴ – 3х³ – 6х² – 11х + 20).

 

       №2. При якому значенні а число 2+ буде коренем многочлена ах² – 8х + 2

Розв’язання. Так як 2+ є коренем многочлена ах² – 8х + 1, то має виконуватись рівність а(2+)² – 8(2+) + 2 = 0.

а(4 + 4 +3) – 16 – 8 + 2 = 0;

а(7 + 4) – 14 – 8 = 0;

а(7 + 4) = 14 + 8;

а(7 + 4) = 2(7 + 4);

а = 2.

 Відповідь: при а = 2.

 

II. Мотивація навчальної діяльності

Як  можна розв’язати  рівняння   х⁵+6х⁴+11х³+11х²+6х+1=0?

Можливі відповіді: розкласти на множники,знайшовши за теоремою Безу або за схемою Горнера корінь.

Якого степеня утвориться рівняння, що треба розв’язати і як діяти далі?

Можливі відповіді:4 степеня і алгоритм повторюємо.

 

Постановка проблеми: рівняння 4 степеня не має у цьому випадку цілих коренів. Чи бажаєте дізнатися інші способи розв’язання алгебраїчних рівнянь?

IІІ. Актуалізація опорних знань

а) Повторення теорії розв'язання рівнянь:

-  Що називається рівнянням? Рівність виразів зі змінною.

-  Що значить розв’язати  рівняння? Знайти число, що перетворює. рівняння у правильну числову рівність або довести, що кореня немає.

- Які види рівнянь ви знаєте? Цілі,дробові, ірраціональні.

 - Які рівняння називаються алгебраїчними?

 Рівняння виду  а₀хⁿ+а₁хⁿ⁺¹+…_а_n-2х²+а_n-1 х+а_n=0

 

б) Повторення прийомів розв'язування рівнянь. Складання опорної схеми.

1) найпростіші (зведення подібних доданків, розкриття дужок, зведення дробів до спільного знаменника, перенесення доданків з однієї частини рівняння в іншу, рішення квадратних рівнянь за формулою, множення (ділення) обох частин рівняння на одне і те ж не рівне нулю число).

 

 

Вправа «Знайди помилку»

Приклад 1

х(х-6)=х | : х≠0

 х-6=1

 х=7

Обґрунтувати помилку. Вирішити рівняння правильно.

 Приклад 2.

= -1

()²=(-1)²

 х+3=1

 х=-2

Обґрунтувати помилку. Що сталося? Вирішити рівняння правильно.

 2) розкладання на множники (формули скороченого множення, угруповання, теорема Безу).

 3) введення допоміжної змінної (слід пам'ятати про ОДЗ самого рівняння і ОДЗ нової змінної).

 4) Нетрадиційні прийоми рішення:

 функціонально-графічний, змішаний.

Усна робота в групах.

Завдання: класифікувати рівняння по виду і за способом вирішення.

1.

2. у²-5у+6=0

3. (х-2)²-2(х-2)-4=0

4. +1=6

^{5. = х}

6. Вказати кількість коренів рівняння 2 | х | = а

7. х³+3х²-4х=0

8. (х-1)²-х²=4-3х

ІІІ.Історичний екскурс

Ви знаєте, що алгебра виникла у зв'язку з рішенням різноманітних задач за допомогою рівнянь. XVі XVI століття увійшли в історію Європи під назвою «епоха Відродження». Для неї характерний розквіт науки і культури. У Європі з'явилися компас, годинник, порох, дешевий папір, книгодрукування. Розвивалася промисловість, що вимагає технічних удосконалень і винаходів, з'являються стимули для розвитку науки. Розквіт науки відбувається головним чином в Італії, Франції, Німеччини. Італійські математики XVI в. зробили велике математичне відкриття. Вони знайшли формули для розв'язання рівнянь 3 і 4 ступенів. Ніколо Тарталья (дитина з дуже бідної сім'ї, мати не могла платити за освіту, тому хлопчик у школі дізнався тільки половину азбуки, всіма іншими знаннями він опанував самотужки). У 6 років він отримав удар мечем в гортань від французького воїна і з тих пір говорив з працею, звідси й прізвисько Тарталья (заїка). Він вивів формули для розв'язання рівнянь 3-го ступеня, але своє відкриття тримав у таємниці.

Джироламо Кардано (медик) займався астрологією, складав гороскопи. Кардано неодноразово звертався до Тартальї з проханням повідомити йому формулу для вирішення кубічних рівнянь і обіцяв зберігати її в секреті. Він не стримав слово і опублікував формулу, вказавши, що Тартальї належить честь відкриття «такого прекрасного і дивного, що перевершує всі таланти людського духу». Учень Кардано Луїджі Феррарі знайшов формули для розв'язання рівнянь 4 ступеня.

Розв’язування   рівнянь

Колективна робота

1.х³-9х+х²–9=0

Спосіб:  розкладання на множники способом групування.

(х³+х²)-(9х+9)=0

 х²(х+1)-9(х+1)=0

 (х+1)(х²-9)=0

 (х+1)(х-3)(х+3)=0    

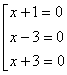           Відповідь: -3; -1; 3.

 

2.  х³-6х²+11х-6=0

Спосіб: розкладання на множники за допомогою теореми Безута за схемою Горнера. По теоремі Безу (залишок від ділення многочлена Р (х) на двочлен (х-а) дорівнює Р (а). Якщо а-корінь многочлена Р (х), то многочлен ділиться на (х-а) без залишку). Розділимо многочлен 3 ступеня на двочлен (х-1).

Один корінь слід шукати серед дільників вільного члена даного многочлена

-6± 1, ± 2, ± 3, ± 6.

 

Цікавий математичний факт - оскільки сума коефіцієнтів многочлена дорівнює 0, то його корінь  є 1.

(два учні біля дошки виконують завдання двома способами)

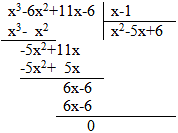
 х³-6х²+11х-6=(х-1)(х²-5х+6)

 (х-1)(х²-5х+6)=0

 х₁=1

 х²-5х+6=0      

За теоремою  оберненою до теореми Вієта  ;   

Відповідь: 1, 2, 3.

 

3. х⁴ +5х³+6х²+5х+1=0

Симетричне рівняння парного степеня. Спосіб: поділ правої і лівої частин рівняння на х².

 Питання - чому це можна зробити? Чи не відбувається втрата кореня?

  х²+5х+6++ = 0

 (х² +)+5(х+) = 0

 х+=у (ОДЗ для допоміжної змінної?)

 х² +=(х+)²-2 = у²-2

 Самостійне розв’язування з наступним оголошенням результатів

у²-2+5у+6=0

у₁=-4; у₂=-1

 х+=-4,  х=-2

 х +=-1, коренів немає.

Відповідь: -2

 

4. х⁵+6х⁴+11х³+11х²+6х+1=0

Цікавий математичний факт - симетричне  рівняння непарного степеня має корінь х = -1. Застосуємо теорему Безу, після поділу многочлена, що стоїть в лівій частині на двочлен (х+ 1) рівняння зводиться до оборотного рівняння парного степеня.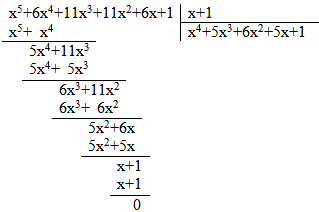

 (х+1)(х⁴+5х³+6х²+5х+1)=0

 

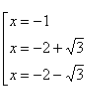
Відповідь:-1, -2

 Поглиблення знань та вмінь учнів по темі «Алгебраїчні рівняння»

Пояснення теоретичної частини вчителем, складання опорної картки.

 

        Рівняння виду (х+а)(х+b)(х+c)(х+d)=A

Якщо a+b=c+d, то (х²+(а+ b)х+ ab) (х²+(с+d)х+ cd)=А

Заміна х²+(а+ b)х=у

 

Робота сильнішого учня біля дошки над прикладом з використанням 

складеної опорної картки         

(х+1)(х+2)(х+4)(х+5)=40

 (х²+6х+5)(х²+6х+8)=40

 х²+6х = у

 (у+5)(у+8)=40

 у²+13у=0

 х²+6х=0  х²+6х=-13, коренів немає, бо D<0

Відповідь: -6, 0.

IV. Повідомлення домашнього завдання та інструктаж щодо його виконання.

Опрацювати опорну картку.

Рівняння виду (х+а)(х+b)(х+c)(х+d)=Aх²

Якщо ab=cd, то (х²+(а+ b)х+ ab) (х²+(с+d)х+ cd)=Ах²  / на х²

                            (х²+(а+ b)х+ ab) (х²+(с+d)х+ cd)=Ах² 

                                         х                         х                х²

Заміна х²+= у

Підготуватися до залікової роботи.

 2х³+8х-х²-4=0

 2х³-12х²+22х-12=0

 6х⁴-35х³+62х²-35х+6=0

 (х+1)(х+2)(х+4)(х+3)=15

         х(х+2)(х+3)(х+5)=20х²

 

V. Підведення підсумку уроку.

          Чи збагатився на нашому уроці багаж ваших знань?

          Чи відчули ви задоволення розв’язуючи рівняння високого рівня складності.

VІ.  Оголошення оцінок за роботу на уроці з урахуванням додаткових балів за домашнє завдання.