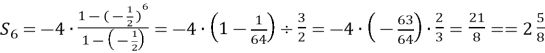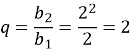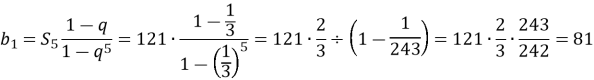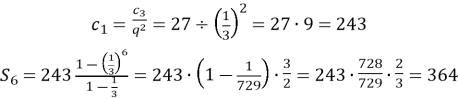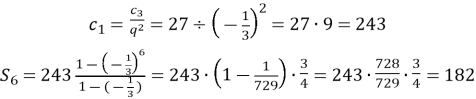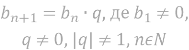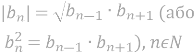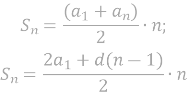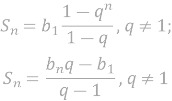Урок з алгебри на тему: "Розв’язування прикладних задач з використанням арифметичної та геометричної прогресій"

Про матеріал

Конспект уроку з алгебри на тему: "Розв’язування прикладних задач з використанням арифметичної та геометричної прогресій". Тип уроку: урок застосування умінь і навичок з теми.

Перегляд файлу

Конспект уроку алгебри в 9 класі

студентки групи МІЕ17Б Чудної Олени

Тема: Розв’язування прикладних задач з використанням арифметичної та геометричної прогресій

Мета:

Навчальна:
- повторення та закріплення основних понять, властивостей арифметичної та геометричної прогресій;
- формування вмінь застосовувати властивості арифметичної та геометричної прогресій до розв’язування прикладних задач.
Виховна:
- виховувати пізнавальний інтерес до математики
- виховувати інтерес до знань;
- виховувати наполегливість.
Розвиваюча:
- розвивати вміння використовувати теоретичні знання на практиці;
- розвивати навички логічного мислення;
- розвивати вміння аналізувати, узагальнювати, порівнювати, робити висновки

Тривалість уроку : 45 хвилин

Тип уроку. Урок застосування умінь і навичок з теми.

Етапи уроку

Організаційний етап (2 хвилини)
Перевірка домашнього завдання (4 хвилин)
Актуалізація опорних знань та мотивація навчальної діяльності учнів (10 хвилин)
Виконання практичних завдань (23 хвилин)
Підсумок уроку (6 хвилини)
Постановка домашнього завдання (2 хвилини)

Хід уроку

Організаційний етап

Привітання вчителя. Перевірка готовності учнів до уроку. Перевірка присутніх на уроці (відмітити в журналі).

Перевірка домашнього завдання

Перевірка наявності виконаного домашнього завдання в зошитах учнів: №815 (1-3), 818, 826, 829 (Алгебра: підруч. Для 9-го кл. загальноосвіт. навч. закл. / О.С. Істер. – Київ : Генеза, 2017. – 264 с.)

№815

Знайдіть суму шести перших членів геометричної прогресії:

1,5; 6; 24;…;
-4; 2; -1;…

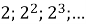
Розв’язання

№818

Використовуючи формулу (2) із цього параграфа, обчисліть суму чисел, що є послідовними членами геометричної прогресії:

Розв’язання

№826

Знайдіть перший член геометричної прогресії , у якої:

Розв’язання

№829

Послідовність – геометрична прогресія, Знайдіть

Розв’язання

Знайдемо та .

За характеристичною властивістю:

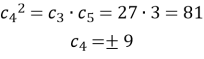Тоді

або

Відповідь:

Актуалізація опорних знань та мотивація навчальної діяльності учнів

Прогресія – це унікальне явище в математиці. Історія її виникнення дуже давня.

Дослідженням прогресій та складанням задач займалося багато математиків протягом багатьох століть. Так, наприклад, в розвиток вчення про прогресії зробили свій внесок Архімед, Піфагор та його учні, французькі математики Леонард Фібоначчі і Баше де Мезіріак, німецькі математики Штіфель, Шюке і Гаусс.

Найдавнішою задачею на прогресії є задача про розподіл хліба, яка записана в Єгипетському папірусі Ринда, яка відноситься до ІІІ ст. до н.е.

Перші задачі на прогресії пов’язані із запитами господарського життя і суспільної практики (розподіл спадщини, одержання винагороди), із спостережень над явищами природи, з досліджень суспільно-економічних явищ.

Сьогодні ж прогресії не втратили своєї актуальності і необхідності в нашому житті і я хочу Вас переконати в цьому на нашому уроці.

Але, перш ніж приступити до цікавих задач, давайте пригадаємо з вами всі необхідні нам знання.

Бліц-опиитування:

Що називається числовою послідовністю? Наведіть приклади.
Які ви знаєте способи задання числових послідовностей?
Сформулюйте означення арифметичної прогресії. Наведіть приклади.
Як знайти різницю арифметичної прогресії?
Сформулюйте властивості арифметичної прогресії.
Запишіть формулу n-ого члена арифметичної прогресії.
Запишіть формулу суми перших n членів арифметичної прогресії.
Що називають геометричною прогресією?
Як знайти знаменник геометричної прогресії?
Сформулюйте властивості геометричної прогресії.
Запишіть формулу n-ого члена геометричної прогресії.
Запишіть формулу суми перших n членів геометричної прогресії.
За якою формулою можна знайти суму нескінченної геометричної прогресії зі знаменником /q/ <1?

Виконання практичних завдань

Прогресії в історії. Хоча ми й живемо в ХХІ столітті, та історичні факти ніколи не втрачають своєї актуальності. Тому, пропоную Вам розглянути Стародавню єгипетську задачу.

Задача 1.

Сто мір хліба треба розділити між п’ятьма людьми так, щоб другий отримав настільки ж більше від першого, на скільки третій отримав більше за другого, четвертий більше за третього та п’ятий більше за четвертого. Окрім того, двоє перших повинні отримати в 7 разів менше, ніж троє останніх. Скільки треба дати кожному?

Розв’язання

Кількість хліба, яку отримав кожний з 5-ти людей, складає арифметичну прогресію, сума 5-ти членів якої дорівнює 100 за умово.

Складемо рівняння:

Тобто,

За умовою, нам відомо, що двоє перших людей отримали в 7 разів менше, ніж троє останніх.

Перші двоє отримають:

Троє останніх:

Тоді за умовою маємо:

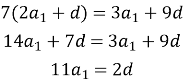
Складаємо систему рівнянь:

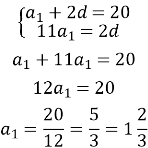
Тепер знайдемо різницю прогресії:

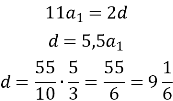
Отже, перша людина отримає мір хліба;

Друга – мір;

Третя – мір;

Четверта – мір;

П’ята –

Відповідь: мір хліба отримають відповідно п’ять людей.

Прогресії в біології. Багатьом здається, що математика, це наука яка далека від природи та тваринного світу, однак це зовсім не так. Наприклад, інтенсивне розмноження бактерій в геометричні прогресії широко застосовується в харчовій промисловості, медицині та фармакології.

Задача 2.

Інфузорії туфельки розмножуються поділом на 2 частини. Скільки інфузорій було спочатку, якщо після 6-го поділу їх стало 320?

Розв’язання

Розмноження туфельок відбувається за правилом геометричної прогресії, де знаменник

За умовою відомо, що

З формули n-го члена послідовності визначимо

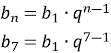
Відповідь: , спочатку було 5 інфузорій туфельок.

Прогресії у фізиці. Ми переконалися, що прогресії застосовуються не тільки в математиці. Також вони є невід’ємними помічниками і у фізиці. Так, за законом геометричної прогресії здійснюється поділ нейтронів при ядерній ланцюговій реакції.

Також, у фізиці є таке поняття як «рівноприскорений рух». Якщо кажуть, що тіло рухається рівноприскорено, то це означає, що відстань, яку воно проходить за кожну наступну одиницю часу збільшується на одну й ту саму величину. Тоді як при рівномірному русі тіло за кожну одиницю часу проходить однакову відстань. Рух може бути і рівносповільненим. Відрізки шляху за рівноприскореного руху утворюють арифметичну прогресію.

Задача 3.

Під час вільного падіння тіло за першу секунду проходить 4,9 м, а за кожну наступну – на 9,8 м більше, ніж за попередню, якщо не враховувати опір повітря. Знайдіть час падіння тіла з висоти 490 м (опором повітря знехтувати).

Розв’язання

Маємо арифметичну прогресію, де ; ;

Розв’язання задачі зводиться до знаходження n.

З формули

Маємо,

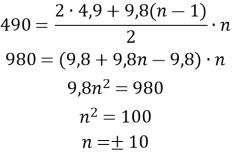
За умовою задачі , сторонній корінь.

Відповідь: час падіння з висоти 490 м становить 10 с.

Прогресії в банківській справі. Існує така думка, що разом з винайденням колеса створення банку стало одним з найважливіших винаходів людства. Перший банк був заснований ще в 1171 році у Венеції. З того часу банки тільки вдосконалювалися.

Ми знаємо основні функції банку:

Зберігання грошових вкладів;
Надання кредитів (позик).

Гадаю, ви знаєте, що якщо помістити певний грошовий вклад до банку, то він виплачуватиме вкладнику деяку суму грошей за те, що користується його капіталом для надання позик. Та чи знали ви, що розмір вкладу зростає за законом геометричної прогресії?

Задача 4.

Вкладник поклав до банку 500 грн. під 8% річних. Скільки грошей буде на його рахунку через три роки?

Розв’язання

Нехай, грн (початковий вклад). Позначимо – кількість грошей на рахунку відповідно в кінці першого, другого та третього року.

Дана послідовність – геометрична прогресія. Знаменником даної прогресії буде , а

Знайдемо , це і буде сума грошей на рахунку вкладника через три роки:

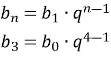
(грн)

Відповідь: через три роки на рахунку вкладника буде 6298,56 грн.

Нинішні ринкові умови вимагають від нас обізнаності у фінансових питаннях, тому фінансова освіченість особистості на першому місці.

Задача 5.

Уявіть, що вам деяка фірма пропонує свої послуги. Щодня ви можете брати у фірми по 100 грн. Але за перший день ви зобов’язані заплатити фірмі 1 коп., за другий – 2 коп., за третій – 4 коп. і т.д. Чи укладете ви з цією фірмою договір не менш ніж на 20 днів за таких умов?

Розв’язання

Виходить, що від фірми ви отримаєте 2000 грн за 20 днів.

З’ясуємо скільки ж грошей будете ви винні фірмі.

З умови бачимо, що виплати утворюють геометричну прогресію, де , а

Для того, щоб знайти суму, яку ви виплатите фірмі, треба порахувати суму перших 20 членів геометричної прогресії:

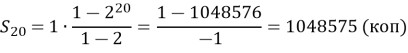
Отже, виходить, що невигідно користуватися послугами такої фірми.

Відповідь: не варто укладати угоду з фірмою за таких умов, так як отримаємо ми 2000 грн, а виплатити маємо 10485,75 грн.

Підсумок уроку

Наш урок добігає кінця. Сподіваюсь, я змогла переконати вас в тому, що математика всюди, а послідовності є дуже корисними в нашому житті.

Чи дізналися ви щось нове для себе?
Чи була ця інформація корисною для вас?

Виконайте, будь ласка, «Перевір себе» (вчитель заздалегідь роздає учням табличку, де вони мають вписати формули).

Арифметична прогресія		Геометрична прогресія
	Рекурентна формула
	Формула n-го члена
	Характеристична властивість
	Формула суми n перших членів
	Формула суми всіх членів геометричної прогресії (\|q\|<1)

Постановка домашнього завдання

Повторити всю теорію, що вивчали на попередніх уроках (послідовності, арифметична/геометрична прогресія та її властивості, сума n перших членів арифметичної/геометричної прогресії, сума всіх членів нескінченно спадної геометрично прогресії); розв’язати задачі (вчитель або дає сфотографувати задачі, або друкує роздатковий матеріал, або надсилає дітям по пошті (гугл-клас, вайбер і т.д.).

Задача 1.Купівля коня.

(Із арифметики Магницького.)

Продавець продав коня за 156 крб. Але покупець, придбавши коня, передумав і повернув його господарю, кажучи: "Нема мені користі купувати за таку ціну коня, який таких грошей не вартий". Тоді продавець запропонував інші умови: "Якщо ціна за коня дуже висока, то купи лише цвяхи для його підков, а коня одержиш безкоштовно на додачу. Цвяхів у кожній підкові 6. За перший дай мені всього 1/4 к., за другий – 1/2 к., за третій - 1к. і т. д..." Покупець, спокусившись низькою ціною та бажаючи безкоштовно придбати коня, прийняв умови, думаючи, що за цвяхи доведеться заплатити не більше 10 крб. На скільки покупець проторгувався?

Розв’язання

За умовою маємо геометричну прогресію, де .

Всього цвяхів з підков буде:

Тобто, в прогресії буде 24 члени.

Нам треба знайти суму цих 24 членів послідовності, це сума яку повинен буде заплатити покупець за підкови:

Покупець проторгувався на:

Відповідь: покупець проторгувався на 41797 крб.

Задача 2.

Мешканець маленького містечка був відомий своєю скнарістю. Коли у нього були справи в повітовому місті, розташованому в 25 км від цього містечка, він звичайно шукав сусідів, які б підвезли його. Одного разу скнара крутився на площі, шукаючи того, хто підвіз би його за спасибі додому. Але цього разу нікого не було і він змушений був шукати платного візника. Скнара обійшов їх усіх, торгуючись з ними і порівнюючи ціни. Один просив 250 крб., другий - 200 крб., третій -150. Усі ці ціни здалися йому занадто високими. Нарешті він помітив візника з убогим візком і жалюгідною шкапою. Коли скнара запитав його скільки він візьме за дорогу, той подивився на землю, почухав потилицю і відповів: "за 1-й кілометр заплати мені 1 коп., за другий - 2 коп, за 3-ій - 4, за 4-ий - 8 і так до кінця шляху."

"От дурний - подумав скнара, ледве стримуючи сміх, - лічить на копійки." Поспіхом він заліз у візок і гукнув:"Згідний! Поїхали!"

Скільки грошей він повинен заплатити за дорогу?

Розв’язання

Маємо геометричну прогресію: 1; 2; 4; 8 …;

Щоб з’сувати скільки коштувати така поїздка, треба знайти суму 25 членів геометричної прогресії (так як їхати 25 км):

Відповідь: скнара повинен буде заплатити за поїздку 335544 крб 31 коп.

Задача 3.

Турист, підіймаючись на гору, за першу годину досяг висоти 800 м, а за кожну наступну годину піднімався на висоту , на 25 м меншу, ніж за попередню. За скільки годин він досягне висоти 5700 м?

Розв’язання

Маємо арифметичну прогресію, де

Задача зводиться до знаходження .

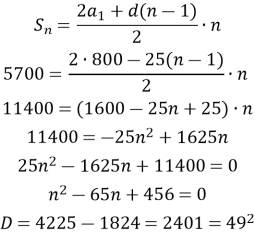
Перевірка:

Відповідь: турист досягне висоти 5700 м за 8 годин.

Задача 4.

У змаганні зі стрільби за кожен промах у серії з 25 пострілів стрілок одержував штрафні очки: за перший промах – одне штрафне очко, а за кожен наступний – на 0,5 очка більше, ніж за попередній. Скільки разів влучив у ціль стрілок, що одержав 7 штрафних очків?

Розв’язання

Маємо арифметичну прогресію, де

Знайдемо з формули суми, таким чином з’ясуємо кількість промахів:

Отже, стрілок зробив 4 промахи. Таким чином в ціль він влучив:

Відповідь: стрілок влучив в ціль 21 раз.

Задача 5.

Одного разу розумний бідняк попросив у скупого багатія притулку на два тижні за таких умов: «За це я тобі першого дня заплачу 1 крб, другого – 2, третього – 3 і т.д., збільшуючи щоденну плату на 1 крб. Ти ж будеш подавати милостиню: першого дня 1 копійку, другого – 2, третього – 4 і т.д., збільшуючи щодня милостиню вдвічі». Багатій з радістю на це згодився, вважаючи умови вигідними. Скільки грошей одержав багатій?

Розв’язання

З’ясуємо спершу скільки карбованців заплатив бідняк багатію. Ми маємо арифметичну прогресію, де