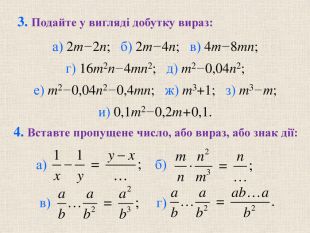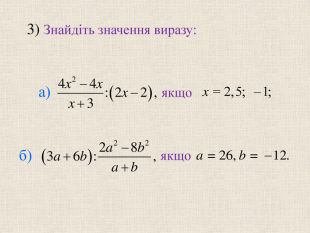Урок з алгебри у 8 класі на тему: "Ділення дробів"
Відкритий урок з алгебри у 8 класі на тему: "Ділення дробів". Конспект уроку складається з пояснення вчителя, а також різноманітних завдань як усної форми так і письмих вправ. А також презентація що відповідає конспекту уроку.
- 1121003.ppt ppt
- urok_15.doc doc
Урок з алгебри у 8 класі
Тема. Ділення дробів
Мета: домогтися засвоєння учнями змісту правила, за яким виконується ділення раціональних дробів, та схеми дій (алгоритму) його застосування під час перетворення частки раціональних дробів на раціональний дріб; сформувати вміння відтворювати зміст вивчених правил та алгоритмів і виконувати дії за цими алгоритмами під час перетворення частки раціональних дробів; вдосконалити вміння щодо скорочення раціональних дробів та множення раціональних виразів.
Тип уроку: засвоєння знань, формування вмінь.
Наочність та обладнання: опорний конспект «Множення та ділення дробів. Піднесення дробу до степеня».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Щоб зекономити час, перевірку домашнього завдання проводимо, звертаючи особливу увагу тільки на ті вправи, які потенційно могли бути складними для учнів.
Як завжди, вчитель в індивідуальному порядку перевіряє роботи учнів, які потребують додаткової педагогічної уваги.
III. Формулювання теми й завдань уроку, мотивація навчальної діяльності учнів
З метою успішного проведення цієї частини уроку можна запропонувати бесіду з учнями, в ході якої знову нагадати про існування певних паралелей між звичайними та раціональними дробами, про логіку вивчення матеріалу 8 класу, пов'язаного з раціональними дробами (була встановлена на попередніх уроках). За цією логікою, наступним (після додавання, віднімання і множення раціональних дробів) вивченим має бути питання про можливість та способи перетворення частки раціональних дробів у раціональний дріб. Отже, у такий спосіб формулюється дидактична мета для наступних 2-х уроків. Для цього уроку вона конкретизується — виноситься питання про правило ділення раціональних дробів (зокрема ставиться питання про подібність цього правила до правила ділення звичайних дробів) та схему (алгоритм) його застосування для перетворення частки раціональних дробів на (нескоротний) раціональний дріб.
Далі складаються завдання на урок: сформулювати правило ділення раціональних дробів та довести його справедливість, розглянути приклади його застосування в різних ситуаціях, скласти орієнтовну схему дій під час перетворення частки раціональних виразів.
IV. Актуалізація опорних знань та вмінь
З метою успішного сприйняття учнями навчального матеріалу уроку перед вивченням нового матеріалу слід активізувати такі знання і вміння учнів: застосування правила ділення і множення звичайних дробів (зокрема повторити спосіб знаходження числа, оберненого до даного раціонального числа, та зробити акцент на відтворенні правил множення і ділення в словесній формі); перетворення цілих виразів (зокрема розкладання многочленів на множники); скорочення раціональних дробів та перетворення добутку раціональних виразів у раціональний дріб.
Виконання усних вправ
-
Обчисліть:
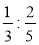 ;
; 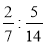 ;
; 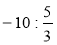 ;
; 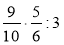 .
.
-
Назвіть число, обернене до:
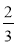 ;
; 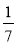 ; 0,1; 1
; 0,1; 1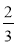 ; 0,(3).
; 0,(3).
- Подайте у вигляді добутку вираз:
а) 2т – 2п; б) 2т – 4n; в) 4т – 8тп; г) 16т2п – 4тп2; д) т2 – 0,04п2;
е) т2 + 0,04п2 – 0,4тп; ж) т3 + 1; з) т3 – т; и) 0,1т2 – 0,2т + 0,1.
- Вставте пропущене число, або вираз, або знак дії:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
V. Засвоєння знань
План вивчення нового матеріалу
- Уявлення про взаємно обернені вирази. Знаходження виразу, оберненого до даного раціонального виразу.
- Правило ділення раціональних дробів. Яка послідовність виконання дій під час перетворення частки раціональних дробів?
- Як застосувати правило ділення раціональних дробів для перетворення частки, що містить раціональний дріб і цілий вираз?
- Приклади застосування правила ділення раціональних дробів.
Вивчення теми «Ділення раціональних дробів» починається з вивчення змісту поняття «взаємно обернені вирази» та способу знаходження виразу, оберненого до даного виразу. При цьому слід наголосити на тому факті, що поняття обернених виразів має по суті той самий зміст, що й поняття взаємно обернених чисел, а тому й спосіб знаходження виразу, оберненого до даного, мало чим відрізняється від способу відшукання числа, оберненого до даного.
Після цього формулюється і доводиться правило ділення раціональних дробів (спосіб доведення якого аналогічний до способу, використаного під час доведення правил виконання дій із раціональними дробами, вивчених на попередніх уроках). Оскільки схема доведення правила знайома учням, можна запропонувати доведення його справедливості самим учням. Засвоєння правила та формування на його основі схеми дій зазвичай відбувається достатньо легко.
Під час вивчення питання про застосування правила ділення раціональних дробів у випадку ділення дробу на цілий вираз, а також ділення цілого виразу на раціональний дріб можна звернутись до досвіду учнів щодо перетворень подібних числових виразів (зі звичайними дробами) та усвідомленого сприйняття ними «скорочених» правил виконання дій у таких ситуаціях. У вигляді формул ці правила можна записати так: ![]() і
і ![]() .
.
Під кінець уроку слід розглянути вправи на застосування вивчених понять та способів дій.
VI. Засвоєння вмінь
Виконання усних вправ
-
Назвіть вираз, обернений до виразу:
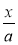 ;
; 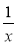 ;
; 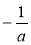 ; 5у;
; 5у; 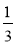 х7; а + 1;
х7; а + 1; 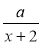 .
.
-
Чи правильно замінено ділення множенням у виразах: а)
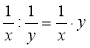 ;
;
б) ![]() ; в)
; в) ![]() ; г)
; г) 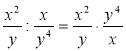 ?
?
-
Подайте у вигляді дробу вирази:
а)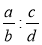 ; б)
; б) 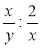 ; в)
; в) 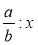 ; г)
; г) 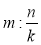 ; д)
; д) 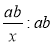 ; є)
; є) 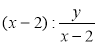 .
.
- Який вираз слід підставити замість крапок, щоб утворилась тотожність:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) 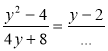 ?
?
Виконання письмових вправ
Для реалізації дидактичної мети уроку слід розв'язати завдання такого змісту.
-
Перетворення частки двох раціональних дробів (різного степеня
складності із застосуванням перетворень, вивчених раніше).
1) Виконайте ділення:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2) Спростіть вираз:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; є)
; є) 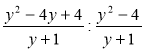 .
.
3) Виконайте ділення:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
- Перетворення частки раціонального дробу та цілого виразу, та навпаки – частки від ділення цілого виразу на раціональний дріб.
1) Виконайте ділення:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2) Виконайте ділення:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3) Знайдіть значення виразу:
а) ![]() , якщо х = 2,5; -1;
, якщо х = 2,5; -1;
б) ![]() , якщо а = 26, b = -12.
, якщо а = 26, b = -12.
- Перетворення суми або різниці раціональних дробів у раціональний дріб.
1) Спростіть вираз ![]() .
.
2) Виконайте дії:
а) ![]() ; б)
; б) ![]() .
.
- Логічні вправи та завдання підвищеною рівня складності для учнів, які мають достатній та високий рівні знань.
1) Виконайте ділення:
а) ![]() ; б)
; б) ![]() .
.
2) Спростіть вираз:
а) ![]() ; б)
; б) ![]() .
.
3) Яке число пропущене?
|
х2 – 8х |
Д |
- 15 |
|
3 – х3 |
Б |
? |
Так само як і на попередніх уроках, учні продовжують одночасно із формуванням умінь виконувати нову дію (ділення раціональних дробів) вдосконалювати свої вміння виконувати інші арифметичні дії з раціональними дробами — додавання, віднімання, множення та скорочення раціональних дробів.
VII. Підсумки уроку
Укажіть правильно виконані дії з раціональними дробами?
1) ![]() ;
;
2) ![]() ;
;
3) ![]() .
.
VIII. Домашнє завдання
- Вивчити правило ділення раціональних дробів та схему його застосування для перетворення частки раціональних виразів.
- Виконайте №150; №155
1

про публікацію авторської розробки
Додати розробку