Урок з алгебри в 11 класі на тему: "Побудова графіків функцій за допомогою похідної. Графіки дробово-раціональних функцій"

Урок 3.Тема: Побудова графіка функції за допомогою похідної.

                                       Графіки дробово-раціональних функцій.

Вчитель КЗШ №45: Ласкіна С.М

Тип: Комбінований.

Мета: Формувати уміння і навики побудови графіка функції за допомогою похідної. Скласти загальну схему дослідження і побудови графіка  дробово-раціональної функції.  Дати поняття асимптоти. Розвивати логічне мислення, уміння аналізувати, порівнювати, бачити аналогію задач. Розвивати навики самостійної роботи.

                           Хід уроку.

Ι- Організаційний момент.

Ι Ι- Перевірка домашнього завдання.

       За звичай у учнів виникають труднощі при побудові такого завдання. 

                       У=.

   Вчитель демонструє побудований графік, і вказує на особливі  лінії – асимптоти, які відіграють велике значення при побудові дробово-раціональних функцій.

ΙΙΙ- Пояснення нового матеріалу.

Асимптота кривої – це пряма, до якої необмежено наближається крива при її віддаленні на нескінченність.

Вертикальні асимптоти:

х=а, якщо  lim f(x)=, при  х→а

Похилі асимптоти:   у=кх+в

                                     к= lim; при х→;

                                     в = lim( f(x)-kx); при х→;

Загальна схема дослідження і побудови графіка  дробово-раціональної функції.                                 

  1.Область визначення функції.

  2. Асимптоти.

  3. Точки перетину з осями координат.

       4.  Парність, непарність функції.

5. Дослідження функції за допомогою Ι похідної.

             Критичні точки.

     Зростання, спадання   функції.

     Точки екстремуму.

1. Дослідження функції за допомогою ΙΙ похідної.( При необхідності)

                Опуклість, угнутість функції.

                Точки перегину.

2.  Додаткові точки.

ΙV- Формування умінь і навиків побудови дробово-раціональних функцій.

          Робота в групах.

Побудувати графіки функцій і перевірити їх побудову за допомогою програми GRAND 2:

      Група 1:    у=

      Група 2:    у=

      Група 3:    у=

Група 1:    у=.

                       Розв’язок.

1.Область визначення функції.

               х

     2. Асимптоти.

              Вертикальні асимптоти:

 х=0,   lim =,якщо  х→0

        Похилі асимптоти:   у=кх+в

               к= lim=1; при х→;

               в = lim( -1х)=0;   при х→;

                       у=х –похила асимптота.

 3. Точки перетину з осями координат.

          У=0: х==-1,6;       (-1,6;0)

      4.  Парність, непарність функції.

                  Функція ні парна, ні непарна.

5. Дослідження функції за допомогою Ι похідної.

             У '=;   =0;

Функція зростає: х і , функція спадає х

                            х=2: у=3.

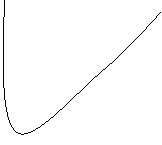5. Графік.

 

 

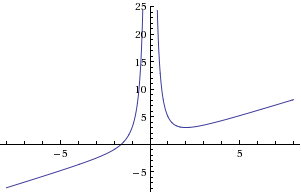
       Група 2:    у=                                    

  1.Область визначення функції.

               х

  2. Асимптоти.

 Вертикальні асимптоти: х=-1,

   lim    =, при   х→-1

  Похилі асимптоти:   у=кх+в

              к= lim=1; при х→;

              в = lim(-1х)=2;   при х→;                     

 у=х+2 –похила асимптота.

  3. Точки перетину з осями координат.

               (0;0); (-3;0)

       4.  Парність, непарність функції.

               Функція ні парна, ні непарна.

5. Дослідження функції за допомогою Ι похідної.

             У '=;

Функція зростає:   х

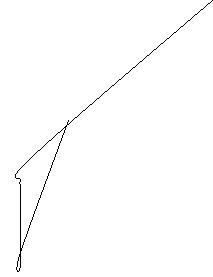
6.Графік:       

                     Група 3:    у=

 1.Область визначення функції.

               х.

2. Асимптоти.

Вертикальні асимптоти:

х=-3,  lim  =, при  х→-3

       х=3,   lim  =. при  х→3

     Похилі асимптоти:   у=кх+в

            к= lim· =0; при х→;

      в = lim()=0;   при х→;

            у=0 –похила( горизонтальна асимптота)

  3. Точки перетину з осями координат.

               (0;); (-2;0)

       4.   Функція ні парна, ні непарна.

5. Дослідження функції за допомогою Ι похідної.

                   У '= ;

Функція спадає:   

           х.

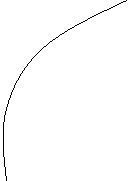
6. Графік.

 

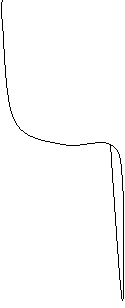
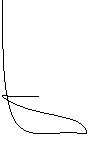
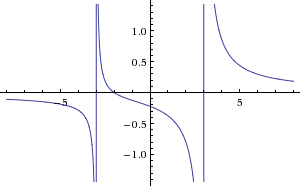
V-Підсумок уроку.

     Питання:

• Як побудувати графік дробово-раціональної функції  за допомогою похідної?
• Яку роль грає Ι похідна?
• Яку роль грає  асимптота ?

 

VΙ- Домашнє завдання.

• Дослідити та побудувати графіки функцій:

         Збірник Сканаві: №15.219, №15.225,        №15.228, №15.230.

 

• Учні об’єднуються ( за бажанням) в творчу групу.

 Група отримує домашнє завдання побудувати різноманітні графіки  дробово-раціональних функцій. Зробити висновки, щодо виду асимптот, в залежності  від степеня чисельника і степеня знаменника дробово-раціональної функції.