Урок з алгебри в 11 класі на тему: "Застосування похідної. Урок-дослідницька робота"

               Урок з алгебри в 11 класі.

Вчитель: Ласкіна С.М

Тема: Застосування похідної. Урок –дослідницька робота.

Тип: Систематизації знань і вмінь.

Мета: Узагальнити знання учнів з теми. Розкрити область застосування

          похідної. Показати,що похідна – засіб дослідження процесів дійсності і    

          сучасного виробництва. Формувати єдину наукову картину світу.

          Розвивати логічне мислення, уміння аналізувати, порівнювати, бачити

          аналогію задач. Розвивати вміння досліджувати, систематизувати

          вивчені факти.

          Виховувати волю та наполегливість у досягненні кінцевого результату.

          Виховувати вміння працювати в групі. Виховувати любов до людини,

          краси, гармонії всесвіту, рідної мови.

Обладнання: комп’ютер, портрети математиків, малюнки,графіки, виставка

                      науково-дослідницьких робіт, рефератів.

                                    Хід уроку.

      I.Організаційний етап.

       За тиждень  до початку уроку  учні об’єдналися в групи, отримали проблемні завдання.

Група 1  « Графіки функцій»

- Група отримала домашнє завдання побудувати різноманітні графіки  дробово-раціональних функцій. Зробити висновки, щодо виду асимптот, в залежності  від степеня чисельника і степеня знаменника дробово-раціональної функції.

Група 2 « Застосування похідної в виробництві»

- Група отримала завдання знайти в магазинах консервну банку оптимальних розмірів. ( Щоб затрати жесті були найменшими, при найбільшому об’ємі.)

 Група 3. « Історичні відомості. Людина.»

-   Група отримала завдання з’ясувати, як розвивалося вчення про диференціальне числення. Які люди внесли вагомий вклад в розвиток цього вчення.

                        Вступне слово вчителя.

                                 (Лунає музика)

Діти, уявіть – Англія, 1666 рік. І. Ньютон, якому лише 23 роки, робить прорив в математиці – відкриває похідну. І все. Життя Європи полетіло так швидко,  що вчені навіть не могли уявити такого. Розвиток науково-технічного прогресу, війни, виготовлення зброї, епідемії і  відкриття цілющого пеніциліну. Запуск космічних ракет і  створення ядерних реакторів -  всьому  основа –диференціальне числення. Від великих досягнень  до великих падінь йшла поряд похідна, кидаючи свої максимуми і мінімуми, похідна , яка так блискавично змінила весь світ.

        Подобно тому, как Архимед, открыв закон рычага, сказал: «Дайте  мне точку опоры, и я здвину Землю», так и  современники  Ньютона говорили: «Составьте нам  дифференциальные уравнения всех движений в природе и  научите их интегрировать, тогда мы будем подобны  Богу, так как с помощью вычислений точно будем знать будущие события.

                                                                                  Д.О.Граве.

 

II. Актуалізація опорних знань.

       Фронтальне опитування.

1). За схематичним графіком функції в околі точки   х охарактеризувати  

    поведінку  f '(х)  та  f(x), визначити вид критичної точки.

 

Орієнтовний вид графіка функції          f '( х) в околі точки х.	Очікувана відповідь. а)  Поведінка f '( х). б) Поведінка f '(x). в) Критична точка х.
	а) f '( х)=0; б)  f '( х) змінює знак   з «+» на «-»; в)  х - точка максимуму.
	а) f '( х)=0; б) f '( х) змінює знак з «-» на «+»; в) х- точка мінімуму.
	а)  f '( х) – не існує; б) f '( х) змінює знак   з «+» на «-»; в) х- точка мінімуму.
	а) f '( х)=0; б) f '( х) змінює знак з «-» на «-»; в) х- точка перегину.
	а) f '( х)=0; б) f '( х) змінює знак з «+» на «+»; в) х- точка перегину.
	а)  f '( х) – не існує; б)  f '( х) змінює знак   з «+» на «-»; в)  х - точка максимуму.

 

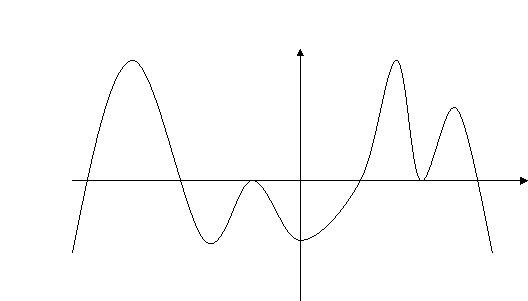
2) Функція y=f(x) визначена на проміжку (-∞;+∞). На рисунку зображено графік  y= f '( х). Укажіть проміжки зростання та спадання функції  y=f(x). Знайти критичні точки функції. Визначити, які з них є точками екстремуму.

 

 

 

 

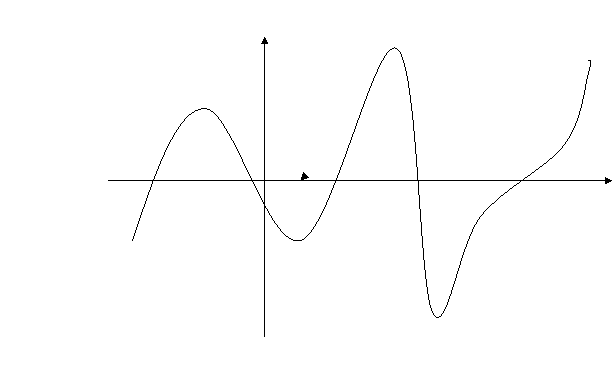
3). Самостійна робота за власним варіантом.

А) Користуючись  зображенням функції y=f(x), укажіть точки екстремуму функції у= f(x). ( підписати на малюнку х і х).

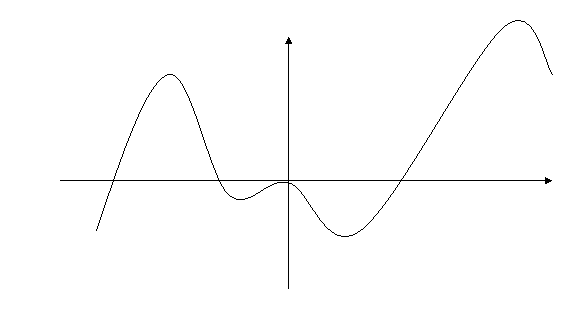
Б).На рисунку зображено графік у= f '(х).Укажіть на рисунку точки екстремуму функції. ( підписати на малюнку х і х).

 

 

 

 

 

 

 

IIΙ – Робота в групах.

Перед початком роботи вчитель зачитує епіграф:

                                                   Найкращий спосіб вивчити що-небудь

                                                   Відкрити його самостійно.

                                                                                 Д.Пойа.

Ι-Графіки функцій - група отримала домашнє завдання побудувати різноманітні графіки  дробово-раціональних функцій. Зробити висновки, щодо виду асимптот, в залежності  від степеня чисельника і степеня знаменника дробово-раціональної функції.

                             Очікуваний результат.

      Учні демонструють побудовані графіки функцій. Роблять висновки:

1. Якщо f(x)- дробово-раціональна функція, у  якої степінь чисельника  більший  на 1 одиницю від  степеня

знаменника то графік функції містить похилу асимптоту.

2. Якщо f(x)- дробово-раціональна функція, у  якої степінь

чисельника дорівнює степеню знаменника, то графік функції містить горизонтальну асимптоту.

3. Якщо f(x)- дробово-раціональна функція, у  якої степінь

чисельника на 2 і більше одиниць більший за степінь знаменника, то графік функції не містить похилих асимптот.

                      4)  Якщо f(x)- дробово-раціональна функція, у  якої степінь

                            чисельника менший степеня знаменника, то графік  функції

                           містить горизонтальну асимптоту   у=0.

Учні  будують на дошці графіки функцій:

1. У=;
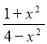2. У=

 

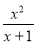
Самостійна робота за власним варіантом:

                   N- Порядковий номер в журналі.

                      Побудувати графік функції:

                              У=

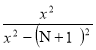
Перевірка побудованих графіків за програмою     GRAND 2.

 

ΙV – Фізкультхвилинка.

Грає легка музика.

Учні закрили очі. Розмахом руки відтворюють графіки функцій.

1. |x|+|y|=1
   • яка утворилась фігура? (квадрат)
   • Яка площа фігури? (2 од.)
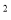   • Який периметр? ( 4од.)

     2) =4;

     3) побудуйте графік приказки: « Як аукнеться , так і відгукнеться».

              ( пряма у=х; вісь ох- «аукнеться», вісь оу – «відгукнеться»).

3. побудуйте графік приказки: « Ні кола, ні двора» ( точка ( 0;0)).
4. « Сім раз відмір – один раз відріж».

 

V- виступ другої групи: застосування похідної в виробництві.

 

                      Деякі люди, коли бачать речі такими, як вони є, питають:

                        «Чому так?». Я бачу речі такими, якими вони ніколи не

                        були, і питаю: « Чому б і ні?».

                                                                                Бернард Шоу.

Учні групи зачитують розв’язані задачі.  Розв’язок однієї  пропонують класу.

           Задача. Визначити розміри циліндричної закритої консервної банки,

                          об’єм  якої  V см, щоб її повна поверхня була найменшою,

                          тобто затрати жесті на її виготовлення були найменшими.

1. Моделювання.

Форма банки – циліндр.

 

2. Математична задача.

   Найти найменше значення функції S(х) на проміжку 0<x<+∞

                      S '(х)=0;

                S '(х)=-; 

                ;

  Тут неможливо порівняти значення функції в критичній точці з її значеннями на кінцях проміжку. Тому з’ясуємо знак похідної зліва і справа від критичної точки.

 

 

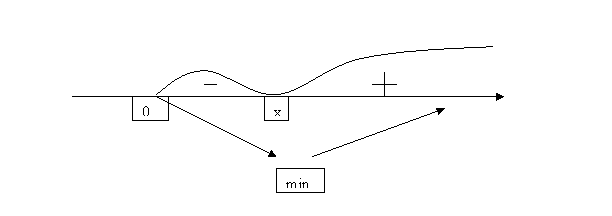
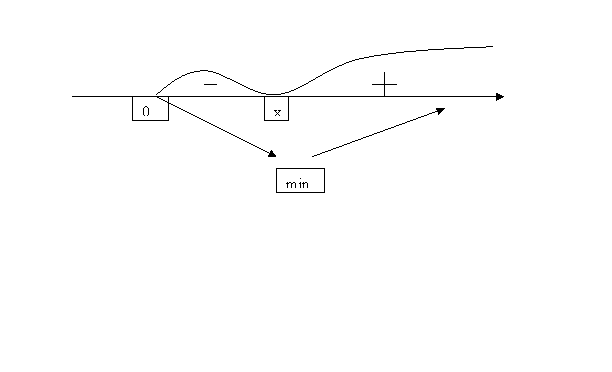
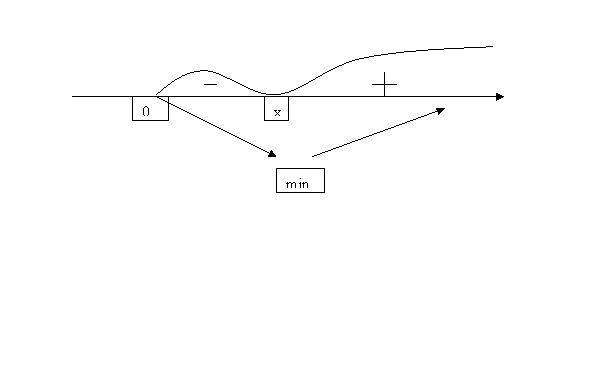
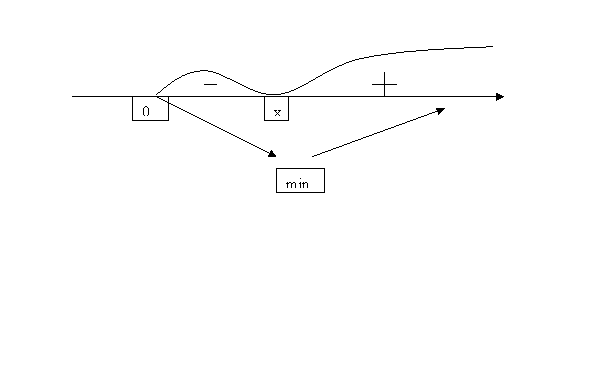
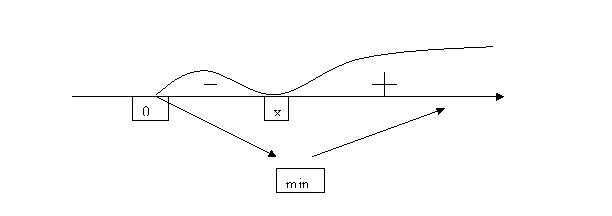
   - діаметр циліндра при якому площа повної поверхні  циліндра буде найменшою.   Н=х.

 

Висновок: осьовий переріз циліндра – квадрат.

 

Учні демонструють консервні банки і розрахунки таблиці.

 

                                            Шпроти.

Реальні розміри.	Оптимальні розміри для банки з найменшою повною поверхнею.	Відсоток  не раціонально використаної жесті.
Діаметр-D=10 см. Радіус –R= 5см. Висота  Н=2см. V=157 см. S=219,8 см	Н=D==5,8 см. S=158,4 см	38%

                                             Сардини.

Реальні розміри.	Оптимальні розміри для банки з найменшою повною поверхнею.	Відсоток  не раціонально використаної жесті.
Діаметр-D=8,5 см. Радіус –R= 4,25см. Висота  Н=5см. V=283,5 см. S=246,9 см	Н=D==7,1 см. S=231см	6%

 Питання учням: Чому виробники несуть такі не раціональні вирази?

      Можливі відповіді учнів:

             -  шпроти мають довжину близько 10см. Тоді висота банки мала

               б висоту 10 см, що за ціною більшою в 5 раз за реальну..(30 грн).

             -   виробнику дуже вигідно, бо покупець оплачує ціну і банки і   риби.

             -  виходить ми купуємо не рибу, а жесть.

              - людині найбільше гармонічнішими здаються прямокутні форми

                (золотий переріз гармонії світу.) Дуже рідко можна побачити банки,

                  переріз яких квадрат.

Вчитель зачитує вислів:

                       Узнать, понять и охватить гармонию научного здания с его

                       недостроенными частями – значит получить такое

                       удовлетворение, какое дают только высшая красота     

                       и, правда.

                                                                      Д.И.Менделеев.

Учитель пропонує учням розв’язати задачу.

                       Еней, герой прославленої  "Енеїди" І.П.Котляревського, після

                       багатьох  пригод приплив до берега і попав у місто.

                                          В тім городі жила Дідона,

                                          А город звався Карфаген,

                                          Розумна пані  і моторна,

                                          Для неї трохи сих імен:

                                          Трудяща, дуже працьовита,

                                          Весела, гарна, сановита.

                        Так розповідає легенда. 825 років до н.е. фінікійська царівна

                         Дідона з невеликим військом вибрала зручне місце на

                         північному узбережжі Туніської заливи. Король Нумібії Ярб

                         погодився продати їй наділ землі, обмежений "шкурою бика".

                         Дідона не розгубилася. Вона  розрізала шкуру на тоненькі

                          смужки. І обмежила територію найбільшої площі. Так був

                         засвоєний Карфаген. Якщо ця територія – прямокутник, то які

                         його розміри?

Розв’язати дану задачу за власним варіантом.    N- Варіант.  

Математична задача.

  Які розміри повинен мати прямокутник найбільшої площі, периметр якого Р= N км.

 Наприклад:   варіант N=Р=22км.

Нехай довжина прямокутника   х км, тоді ширина ( 11-х)км.

S(х)=х·(11-х)=11х-х;     0<S<∞

S'(х)=0;

S'(х)=11-2х;

11-2х=0;

Х=5,5

  Тут неможливо порівняти значення функції в критичній точці з її значеннями на кінцях проміжку. Тому з’ясуємо знак похідної зліва і справа від критичної точки.

  Похідна змінює знак з «+» на «-», значить  х - точка максимуму.

Х=5,5 (км) – довжина прямокутника.

11-5,5=5,5(км)- ширина прямокутника.

Висновок – серед прямокутників найбільшу площу має квадрат.

 

VΙ- виступ третьої групи. Історичні відомості. Людина.

 

                                       Вам поклоняюсь, вас желаю, числа!

                                            Свободные, бесплотные, как тени,

                                            Вы радугой связующей повисли

                                            К раздумиям с вершины вдохновенья!

                                                                                     В.Я.Брюсов.

1-учень.      Відкриттю похідної і основ диференціального числення передували роботи французького математика і юриста П. Ферма (1601-1665), який в 1629 році пропонував способи знаходження найбільших і найменших значень функцій, проведення  дотичних до довільних кривих; роботи Рене Декарта (1596-1650), який розробив метод координат і основи аналітичної геометрії.

   Тільки в 1666 році англійський математик і фізик І.Ньютон (1643-1727) і трохи пізніше відомий математик Г.Лейбніц (1646-1716) незалежно один від одного побудували теорію диференціального числення. Ньютон похідну називав «флексією», а саму функцію «флюєнтною»( текучою).

    Термін «lim» вперше знаходимо у Ньютона в 1686 році.

В 1696 році француз Франсуа Антуан де Лопіталь видає перший в світі друкований підручник з диференціального числення.

 В 1755 році Л.Ейлер написав підручник «Диференціальне числення».

В 1797 році французький математик Жозеф Луї  Лагранж (1736- 1813) ввів термін «похідна», позначення у' .

    За допомогою похідної було вирішено цілий ряд задач теоретичної механіки, фізики і астрономії. Так вчені передбачили повернення комети Галлея, що стало тріумфом науки XVΙΙΙ століття.

 2- учень.      Вчені – такі люди, як ми з вами.

    Лопіталь мав поганий зір, мріяв стати офіцером артилерії. З дитинства захоплювався математикою. Малював криві лінії і мріяв записати їх рівняння.

    Французький математик Жозеф Луї  Лагранж був на концерті. Сидів дуже зосередженим. Хтось спитав його, чим йому подобається ця музика?

     -  Подобається тим, що я усамітнююся. Слухаю перші три такти, а на четвертому уже нічого не помічаю, думки несуть мене. Таким чином я розв’язав вже не одну складну задачу.

3-учень. Людина шукає гармонію і порядок,  пробує найти рівновагу між наукою і почуттями. Я думаю, що можливо і серед нас будуть вчені, які зможуть зробити світ красивішим і гармонічнішим.

 

                                                        Нельзя быть математиком, не будучи

                                                         одновременно  поэтом в душе.

                                                                                 С.Ковалевская.

Учні  читають власні вірші.

* * *     

      Я беру производную –

      Каково удивление,

      Мир меняется  весь

      Вижу скорость

      Его изменения.

      Мир из хаоса вдруг

      Превращается в схемы

      У гармонии тоже

      Есть свои теоремы.

* * *

  Жизнь человека, словно синусоида,

  То вверх летишь, то падаєшь  ты вниз,

   Когда настанет максимум и минимум,

   Когда  исчертишь ты  последний лист?

               А мудрецы свой график исправляли ,

                Чтоб приближался он к стремительной прямой,

                 Чтобы как птицы от нуля взлетали

                  Без перегибов мысли над землей.

VΙΙ- Підсумок уроку.

Вправа мікрофон:     Де застосовується похідна?

        Бажані відповіді:

• При побудові графіків функцій.
• При розв’язуванні рівнянь.
• При розв’язуванні нерівностей.
• При доведенні тотожностей.
• При розв’язуванні задач на знаходження найбільших і найменших значень.
• При знаходженні рівняння дотичної.
• При обчисленні границь. Правіло Лопіталя.
• При розв’язуванні  задач з фізики, астрономії  тощо.

 

VΙΙΙ-Заключне слово вчителя.

На екрані комп’ютера  зображення людини з розрахунками золотого перерізу.

      - Ось вона -  Людина! Людина накреслена математикою, але у якої свої особливі думки, свій світ, своя доля. Людина – розумна!. Вона навчилася керувати ракетами і, можливо колись, навчиться управляти собою, своєю похідною.

               Вчитель виставляє оцінки. Визначає  кращого учня уроку і надає йому право написати і захистити на районному конкурсі науково-дослідницьких робіт  наукову роботу з теми: «Застосування похідної».