Урок з алгебри в 8 класі.Тема уроку : узагальнення і систематизація знань з теми “Квадратні рівняння “ .
Урок алгебри в 8 класі
Тема уроку : узагальнення і систематизація знань з теми “Квадратні рівняння “ .
Мета уроку : провести закріплення навичок розв'язування квадратних рівнянь , теореми Вієта , і теореми оберненої до теореми Вієта , звернути увагу учнів на розв'язування квадратних рівнянь виду ax+ bx + с = 0, в яких a+b+c=0; розвивати навички розв'язування неповних квадратних рівнянь , а також задач які розв'язуються за допомогою квадратних рівнянь; сприяти розвитку у учнів уміння узагальнювати вивчене ; закріплення навичок самостійної роботи ; грамотної математичної мови.
Урок алгебри в 8 класі
Тема уроку : узагальнення і систематизація знань з теми “Квадратні рівняння “ .
Мета уроку : провести закріплення навичок розв’язування квадратних рівнянь , теореми Вієта , і теореми оберненої до теореми Вієта , звернути увагу учнів на розв’язування квадратних рівнянь виду ![]() ax
ax![]() + bx + с = 0, в яких a+b+c=0; розвивати навички розв’язування неповних квадратних рівнянь , а також задач які розв’язуються за допомогою квадратних рівнянь; сприяти розвитку у учнів уміння узагальнювати вивчене ; закріплення навичок самостійної роботи ; грамотної математичної мови.
+ bx + с = 0, в яких a+b+c=0; розвивати навички розв’язування неповних квадратних рівнянь , а також задач які розв’язуються за допомогою квадратних рівнянь; сприяти розвитку у учнів уміння узагальнювати вивчене ; закріплення навичок самостійної роботи ; грамотної математичної мови.
Тип уроку : урок узагальнення і систематизації знань.
Обладнання : портрет Вієта , різнорівневі картки, таблиці, формули .
Хід уроку :
- Вступ. Пояснення теми і мети уроку.
- Перевірка домашнього завдання , яке було попередньо записане одним з учнів на дошці .
- Математичний диктант.
- –12 + 7 + 2 = 3 .
- – (2a –4) = - 2a + 4.
-
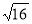 =4.
=4.
-
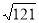 =11.
=11.
-
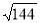 =12.
=12.
-
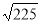 =15.
=15.
- Записати загальний вигляд повного незведеного квадратного рівняння.
- Записати квадратне рівняння, у якого перший коефіцієнт 3 , другий коефіцієнт –5 , а вільний член 1 .
-
Розв’язати рівняння : x
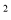 - 4 = 0, x=
- 4 = 0, x=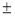 2.
2.
-
Розв’язати рівняння : 2x
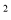 = 18 , x=
= 18 , x=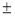 3.
3.
-
Розв’язати рівняння : x
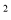 - 2x = 0 , x=0;2.
- 2x = 0 , x=0;2.
Після перевірки відповідей на дошці , робиться висновок про рівень підготовки учнів.
- На дошці вивішені плакати з 12 квадратних рівнянь:
1) x![]() + x – 2 = 0 -2 ; 1,
+ x – 2 = 0 -2 ; 1,
2) 4x![]() + x –3= 0 1 ; -
+ x –3= 0 1 ; -![]() ,
,
3) 5x![]() - 7 x + 4 = 0
- 7 x + 4 = 0 ![]() Ø,
Ø,
4) x![]() + 2x – 3 = 0 -3 ; 1 ,
+ 2x – 3 = 0 -3 ; 1 ,
5) 2x![]() – 6x = 0 0 ; 3,
– 6x = 0 0 ; 3,
6) 15x![]() = 0 0,
= 0 0,
7) x![]() - x – 2 = 0 -1 ; 2 ,
- x – 2 = 0 -1 ; 2 ,
8) 3x![]() –12 = 0 - 2 ; 2 ,
–12 = 0 - 2 ; 2 ,
9) x![]() – 144 = 0 -12 ; 12 ,
– 144 = 0 -12 ; 12 ,
10) 15x![]() - 2 x – 8 = 0 -
- 2 x – 8 = 0 -![]() ;
; ![]() ,
,
11) x![]() + 6x +8 = 0 -4 ; -2 ,
+ 6x +8 = 0 -4 ; -2 ,
12) 2x![]() + x – 3 = 0 -
+ x – 3 = 0 - ![]() ; 1 .
; 1 .
Учні усно виявляють тип кожного квадратного рівняння .
Повне незведене 2 ; 3 ; 10 ; 12 .
Повне зведене 1 ; 4 ; 7 ; 11.
Неповне 5 ; 6 ; 8 ; 9 .
Три учні ідуть до дошки розв’язувати квадратні рівняння , вибираючи будь-які три з них.
- Всі інші учні усно згадують способи розв’язування квадратних рівнянь :
а) повні квадратні рівняння :
- через дискримінант ;
- за властивістю коефіцієнтів :
б) повні зведені квадратні рівняння :
- за теоремою Вієта ;
- за теоремою оберненою до теореми Вієта:
в) неповні квадратні рівняння :
- за спеціальними методами.
Учні роблять усні повідомлення . ( додаток 1 , додаток 2 )
Учні отримують індивідуальні картки, сильні учні – ускладнені завдання , учні з низьким рівнем - картки з допомогою.
Всі інші учні розв’язують приклади з дошки .
6. Розв’язування задачі з підручника № 398.
Коль задачу мы решаем,
Уравненье составляем !
Хочешь бродом , хочешь вплавь-
Уравнение составь !
В нем и кроется секрет!
Корень – он и есть ответ!
Если хочешь быть доволен,
То ищи скорее корень!
Задача:
На вишні заквітчаній кілька гілок ,
На них сіли порівну двісті бджілок .
Коли б на п’ять менше гілок розцвіло ,
На кожній би бджіл на дві більше було б.
То ж скільки гілок на цій вишеньці гожій ,
І скільки бджілок працювало на кожній ?
Розв’язання : нехай було Х гілок , тоді (Х-5) було б менше , на Х сіло б ![]()
![]() , або
, або ![]() , їх різниця дорівнює 2. Складемо рівняння :
, їх різниця дорівнює 2. Складемо рівняння :
![]() -
-![]() = 2 ;
= 2 ;
![]() = 0;
= 0;
ОДЗ: Х![]() ; 5;
; 5;
-2Х![]() + 10 Х +1000 = 0 ;
+ 10 Х +1000 = 0 ;
Х![]() -5Х – 500 = 0 ;
-5Х – 500 = 0 ;
Д= 25+2000=2025=45![]() ;
;
Х![]() =
=![]() =-20; 25;
=-20; 25;
-20 – сторонній корінь.
200: 25 = 8 (бдж.)
Відповідь: 25 гілок , 8 бджілок.
- Підсумки уроку:
Виставлення оцінок учням , відмітити найбільш активних . Запис домашнього завдання в щоденники .
заключне слово : таким чином ми з вами навчились розв’язувати квадратні рівняння усіх типів , а також складні квадратні рівняння за допомогою яких розв’язують різні задачі . І не тільки математичні, за допомогою рівнянь розв’язують задачі з хімії, з фізики. Ми узагальнили знання про рівняння , з’ясували їх застосування на практиці та в інших науках. І ще раз переконались, що математика, як і будь-яка інша наука, не розвивається сама, всі відкриття в ній роблять люди. Так свій внесок у розвиток вчення про рівняння зробили Евклід, Діофант, аль-Хорезмі, Омар Хайям, Ф. Вієт та інші вчені. І ці люди не обмежувались лише математикою, вони були високо освіченими і всебічно розвинутими, до чого повинна прагнути кожна людина.
Додаток 1.
Рівняння.
Рівняння-це два вирази, з’єднанні знаком рівності; в ці вирази входять одна або декілька змінних, які називаються невідомими. Розв’язати рівняння-означає знайти всі значення невідомих, при яких воно обертається в вірну рівність, або встановити, що таких значень не існує.
Рівняння – одне з найважливіших понять в математиці. В більшості практичних або наукових завдань, де деяку величину неможливо безпосередньо виміряти або обчислити за відомою формулою, вдається скласти співвідношення, яким воно задовольняє. Так отримують рівняння для визначення невідомої величини.
Розвиток методів розв’язування рівнянь, починаючи з зародження математики, як науки, довго було основним предметом вивчення алгебри. Звичний нам буквений запис рівняння склався в 16-у сторіччі; традиція позначати невідомі останніми буквами латинського алфавиту-x, y, z, а відомі величини (параметри) першими - а, в, с, іде від французького вченого Рене Декарта.
Додаток 2.
Франсуа Вієт (1540-1603).
Французький математик. За професією – юрист. В 1591 році ввів буквені позначення не тільки для невідомих величин, але і для коефіцієнтів рівнянь, завдяки цьому стало вперше можливим вираження властивостей рівнянь і їх коренів загальними формулами. Йому належить встановлення єдиного прийому розв’язання рівнянь другої, третьої і четвертої степенів. Серед відкриттів сам Вієт високо оцінив встановлення залежності між коренями і коефіцієнтами рівнянь. Для наближеного розв’язування рівнянь з числовими коефіцієнтами Вієт запропонував метод, схожий з методом, який пізніше запропонував Ньютон. В тригонометрії Вієт дав повний розв’язок задачі про визначення всіх елементів плоского або сферичного трикутника за трьома даними, знайшов розкладання cos nx і sin nx за степенями cos x і sin x. Вієт вперше розглянув нескінченні добутки. Праці Вієта написані важкою мовою і тому отримали менше розповсюдження, ніж


про публікацію авторської розробки
Додати розробку
