Урок-квест "Квадратні рівняння"

Про матеріал

Єдиний шлях, що веде до знань – це діяльність. Бернард Шоу

Ці слова відображають суть уроку-квесту, бо діти активно працюють в команді, рухаються по станціям, закріплюють вивчене і відкривають для себе нове! Вони вчаться перезентувати свої досягнення, працювати в команді.

Перегляд файлу

Лисенко Олена Євгенівна

Урок-квест «Квадратні рівняння»

Мета: систематизувати здобуті знання, формувати практичні навики їх використання, вміння аналізувати, критично мислити, працювати в команді, виховувати відповідальність, упевненість в собі, волю до перемоги, досягнення успіху у житті

Обладнання: мультимедійна система, ресурс Learningapps, додаток Документ Google, програма для зчитування QR-коду, картки із завданнями, маршрутні листи для команд

Місце проведення: кабінет математики

Підготовча робота: клас поділений на 6 команд, кожна команда обирає капітана; учнівські парти розміщені так, щоб дітям зручно було працювати на станціях; на партах назви станцій «Дослідження», «Теорема Вієта», «Історична», «Інтерактивна», «Цікаве рівняння», «QR-код»; кожна команда працює вдома по історичному матеріалу, пов’язаному з темою «Квадратні рівняння»; на Google Диску створено секторну діаграму з спільним редагуванням для підведення підсумків квесту; підготувати на станції консультантів

Єдиний шлях, що веде до знань – це діяльність.

Бернард Шоу

Хід уроку

І. Організаційний момент

Учитель: Доброго дня, діти! Ми сьогодні проведемо з вами урок-квест. Що таке квест, я впевнена, ви знаєте. Поділіться своїми знаннями. (Діти розповідають, що вони розуміють під словом «квест»).

Отже, команди готові до роботи, і ми можемо вирушати в подорож по країні «Квадратні рівняння». Не забудьте взяти з собою гарний настрій, спрямований тільки на перемогу; відповідальність, взаємоповагу і бажання зміцнити свої знання і відкрити для себе нове! Кожна команда рухається по шести станціях, перемагає та, яка перша відкриє всі таємниці! Капітани команди, отримайте маршрутні листи (Додаток 1) і починаємо подорож!

ІІ. Подорож по станціях

«Цікаве рівняння»

Розв’яжіть рівняння:

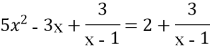
Консультанти перевіряють правильність і роблять відмітку у маршрутному листі кожної команди. (Відповіді подані у Додатку 2).

«Дослідження»

Що буде, якщо в квадратному рівнянні ах² + bx + c = 0 поміняти

місцями a і c?

Для дослідження використайте рівняння:

х² – 6х + 5 = 0

5х² – 9х – 2 = 0

«Інтерактивна вправа»

Розділіть рівняння на групи по кількості їх коренів.

Вправа виконується на комп’ютері, перевіряється автоматично.

https://learningapps.org/view4563471

«Теорема Вієта»

Заповніть таблицю, використовуючи теорему Вієта.

Рівняння	Сума коренів	Добуток коренів
х² – 6х + 5 =0
3х² + 3х ‒ 5 =0
0,2х² – 8х + 5 =0
	8	12

«Історична станція»

Встановіть відповідність між історичним фактом і особистістю.

Питання	Відповіді
Вперше навів приклади розв’язування неповних квадратних рівнянь	А. Вієт
2. Відкрив правило знаходження коренів рівняння ах² +bх = с	Б. Діофант
3. Вивів формулу залежності коренів рівняння від коефіцієнтів	В. Брахмагупта
4. Вивів загальне правило розв’язування квадратних рівнянь	Г. Штифель
5. Запропонував формулу дискримінанта	Д. Піфагор
	Е. Сільвестр

$C:\Users\Yagotin\Desktop\static_qr_code_without_logo.jpg$
«QR- код»

Прочитайте вислів і поясніть його важливість.

ІІІ. Підсумок уроку

Команди звітуються про виконані завдання, розповідають, що було найважче виконати, над чим ще треба попрацювати.

На якій станції було найцікавіше працювати показують на секторній діаграмі, яка створена в Документі Google і для якої відкритий доступ для спільного редагування. Учні виходять до інтерактивної дошки і перетягують трикутник до певного сектора.

Посилання для спільного доступу

Додаток 1

Маршрутні листи команд

Команда № 1

Станції	Відмітка про виконання	Бали
Історична
Дослідження
Інтерактивна вправа
QR - код
Теорема Вієта
Цікаве рівняння

Команда № 2

Станції	Відмітка про виконання	Бали
Дослідження
Інтерактивна вправа
QR - код
Теорема Вієта
Цікаве рівняння
Історична

Команда № 3

Станції	Відмітка про виконання	Бали
Інтерактивна вправа
QR - код
Теорема Вієта
Цікаве рівняння
Історична
Дослідження

Команда № 4

Станції	Відмітка про виконання	Бали
QR - код
Теорема Вієта
Цікаве рівняння
Історична
Дослідження
Інтерактивна вправа

Команда № 5

Станції	Відмітка про виконання	Бали
Теорема Вієта
Цікаве рівняння
Історична
Дослідження
Інтерактивна вправа
QR - код

Команда № 6

Станції	Відмітка про виконання	Бали
Цікаве рівняння
Історична
Дослідження
Інтерактивна вправа
QR - код
Теорема Вієта

Додаток 2

Відповіді

Станція «Цікаве рівняння»

х = -0,4, х ≠ 1.

Станція «Історична»

– Б, 2 – В, 3 – А, 4 – Г, 5 –Е.

«Теорема Вієта»

Рівняння	Сума коренів	Добуток коренів
х² – 6х + 5 =0	6	5
3х² + 3х ‒ 5 =0	1
0,2х² – 8х + 5 =0	40	25
	8	12

Станція «Дослідження»

Корені будуть оберненими до коренів даного рівняння

Станція «QR- код»

Вислів:

Найкращий спосіб вивчити що-небудь – це відкрити самому.

Д. Пойа

docx

Завантажити

Зберегти на потім

Додав(-ла)

Лисенко Олена Євгенівна

Пов’язані теми

Алгебра, 8 клас, Розробки уроків

До підручника

Алгебра 8 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)

До уроку

§ 3. Квадратні рівняння

Додано

8 липня 2018

Переглядів

1548

Оцінка розробки

Відгуки відсутні