Урок з геометрії для учнів 7класу з теми : "Основні задачі на побудовуу. Розв'язування задач на побудову"

Тема. Основні задачі на побудову . Розв’язування задач на побудову.

Мета.

Сформувати  в учнів уміння мислити образами , потребу в графічних знаннях та вміннях , прагнення до спілкування засобами графічних зображень, що є необхідним у процесі адаптації до життя та діяльності у високотехнологічному суспільстві. 

Учні повинні засвоїти загальний план розв'язання задач на побудову, навчитися виконувати дії з цим планом і вміти для побудови застосовувати циркуль і лінійку та навчитися будувати  малюнки у програмі «DG- пакет динамічної геометрії». 

Розвивати навики самостійної роботи дослідницькі навики формування вмінь аналізувати , узагальнювати вивчені факти. 

Виховувати  охайність записів та  виконання побудови малюнків, пізнавальний  інтерес до математики, спостережливість, соціальну компетентність, взаємодопомогу,відповідальне ставлення до навчання.

Тип уроку:    засвоєння нових  знань  та практичних вмінь .

Хід уроку І. Організаційна частина.

ІІ. Мотивація навчальної діяльності .

    Математики Стародавнього світу, як правило, багато задач розв’язували геометричним способом, використовуючи різні спеціальні прилади. Наприклад, вони могли за допомогою циркуля і лінійки порівняно легко побудувати суму і різницю двох відрізків, поділити кут навпіл, помножити відрізок на звичайний дріб. 

Постановка проблемного запитання.

Чи кожна задача на побудову має розв’язання ?

ІІІ. Вивчення нового матеріалу.

 Мета  розв’язування  здач на побудову – це побудова геометричних фігур із заданими властивостями. В геометрії виділяють задачі на побудову, які можна ров’язувати тільки за допомогою двох інструментів: циркуля та лінійки без масштабних ділень. Лінійка:

üдозволяє провести довільну пряму; 

üпобудувати пряму, яка проходить через дві дані точки.

 Циркуль:

üможна провести коло довільного радіуса; 

üколо з центром в даній точці і радіусом, що дорівнює даному відрізку.

Розв’язати задачу на побудову означає :

üзнайти послідовність елементарних побудов , після виконання яких шукана фігура вважається побудованою ;

üдовести , що ця фігура задаовільняє умову задачі.

Розв’язування  задач на побудову складається з чотирьох етапів :

Øаналіз( визначення плану побудови шуканої фігури );

Øпобудова ( здійснення плану , розробленого в ході аналізу );

Øдоведення (встановити, що побудована фігура дійсно задовольняє умові задачі);

Ø дослідження (встановлення кількості розв’язків , або обґрунтування неможливості побудови шуканої фігури ).

Розглянемо основні геометричні побудови:

1) Побудова відрізка , що дорівнює даному.

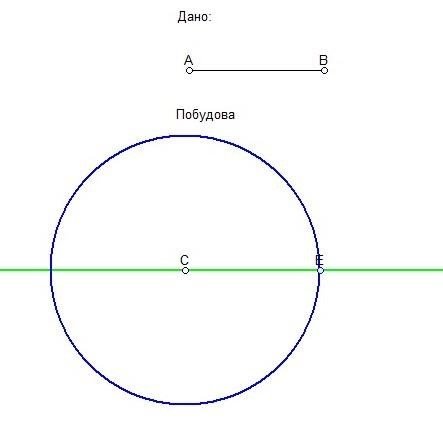
§     проводимо пряму  , позначаємо на ній точкуС;

§     з точки С радіуса r=AB проводимо коло, отримали точку Е ( точка перетину кола і прямої ); §  відрізок АВ=СЕ.

2)       Побудова кута , що дорівнює даному.

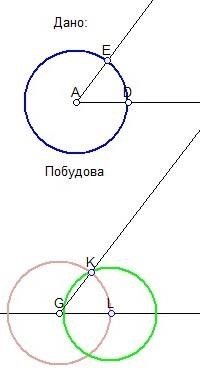
§  проводимо  пряму позначаємо на ній точку G;

§  з точки G проводимо коло  радіуса r=AD, отримали точку L  ( точка перетину кола і прямої);

§  з точки L проводимо коло  радіуса r=DE, отримали точку K  ( точка перетину  двох кіл );

§  з точки G проводимо промінь GK.

Довести :кут А= куту G

Доведення

Розглянемо  трикутник АДЕ і трикутник GLK:

АД=GL ( як радіуси одного кола)

АЕ=GK(як радіуси одного кола )

ЕД=KL(як радіуси описаного кола )

Отже , трикутник ADE дорівнює трикутнику GLK за третьою ознакою рівності трикутників.

3)       Побудова бісектриси кута.

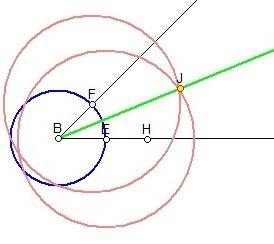
§  проводимо коло довільного радіуса, отримали точки  F і Е( точки перетину кола і сторін кута);

§  з точок F і Е проводимо кола радіуса r=BH, отримали точку J (точка перетину двох кіл );

§  проводимо промінь BJ.

4)       Побудова перпендикулярних прямих.

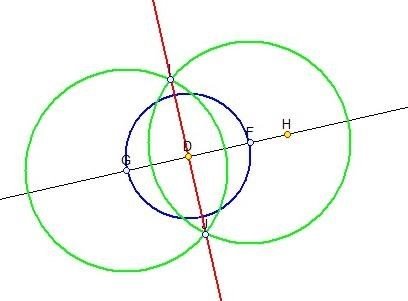
§  проводимо пряму позначаємо на ній точку Д;

§  з точки Д проводимо коло довільного радіуса, отримали точки FіG (точки перетину кола і прямої );

§  з точок FіG проводимо кола радіуса r= DH, отримали точки I та J (точки перетину кіл );

§  через точки  I та J  проводимо пряму. 5)Побудова середини відрізка.

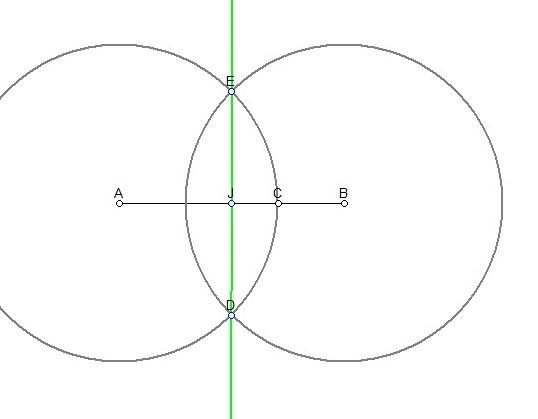
§  на відрізку АВ позначаємо точку С;

§  з точок А та В  проводимо кола радіуса r=AC, отримали точки Е і Д ( точки перетину кіл );

§  через точки Е і Д проводимо пряму.

IV.   Закріплення матеріалу.

 Робота учнів в групах :

Задача1. За даним малюнком сформулювати задачу  та описати хід побудови.

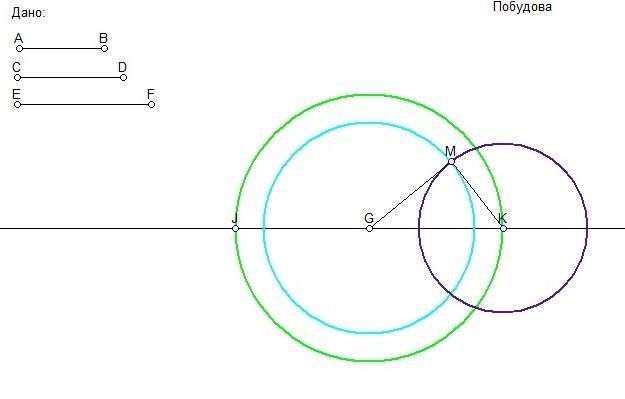
Задача2. За даним малюнком сформулювати задачу  та описати хід побудови.

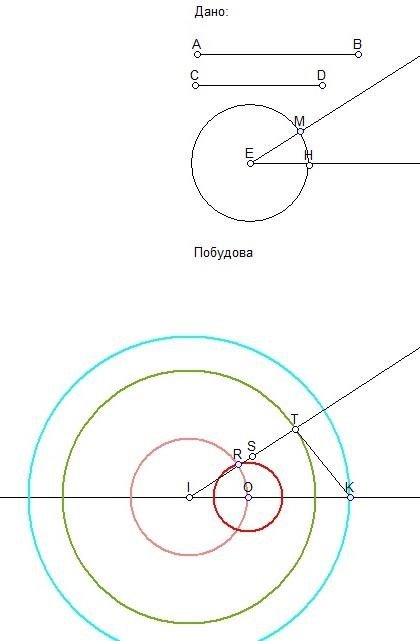
Задача3. За даним малюнком сформулювати задачу  та описати хід побудови.

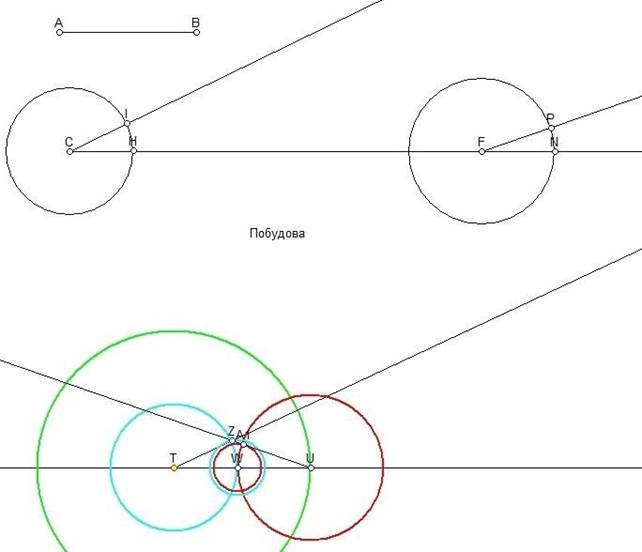
V.      Самостійна робота учнів (індивідуальна ).

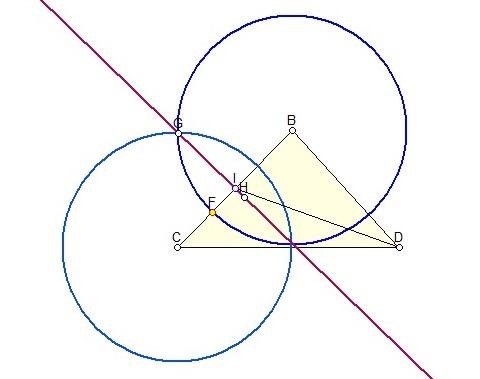
  Завдання1.Побудувати медіану трикутника.

Відповідь:

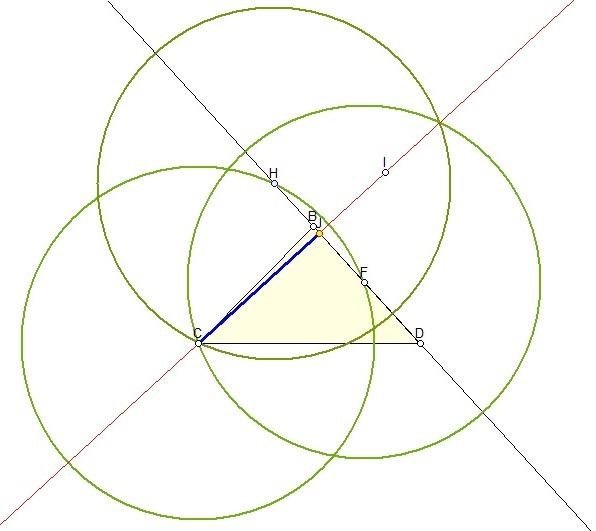
Завдання2. Побудувати висоту трикутника Відповідь:

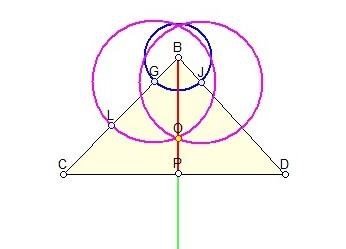
Завдання3.Побудова бісектриси трикутника. Відповідь:

VI.   Підсумок уроку 

Дати відповідь на запитання  (міні-тест):

1.     За допомогою яких приладів можна виконувати задачу на побудову ?

Ø лінійка ;

Ø косинець і лінійка ; Ø лінійка і циркуль ; Øциркуль.

2.     Чи можна за допомогою лінійки побудувати відрізок АВ=СД. Øтак; Øні. 3.Скільки етапів містить задача на побудову ?

Ø 5;

Ø 3;

Ø 4; Ø 2.

VII. Домашнє завдання.

Розв’язати задачі:

v  Побудувати кут130⁰.

v  Дано тупокутний трикутник. Побудуйте всі його висоти.

v  Побудувати рівнобедрений трикутник за бічною стороною і кутом при основі.