Урок з геометрії 7-А клас

Тема:  Коло, описане навколо трикутника.

Мета:  Ввести поняття серединного перпендикуляра,  описаного навколо трикутника; відпрацювати навички розв’язування задач.

Розвивати логічне мислення.

Виховувати увагу, активність, швидкість реакції та доброзичливість.

Хід роботи

I. Актуалізація опорних знань учнів

Вказати правильну відповідь (обмін зошитами)

а) 1. Найпростішою геометричною фігурою є...

А) Трикутник. Б )Точка. В) Ламана. Г) Коло.

2.Кути, у яких одна сторона спільна, а дві інші є доповняльними променями називаються...

А) Вертикальні. Б) Прямі. В) Суміжні. Г) Гострі.

3.Трикутник, у якого довжини всіх сторін рівні називається...

А) Гострокутний. Б) Рівнобедренний. В) Рівносторонній. Г) Прямокутний

4.Кути, сторони якого є доповняльними променями до сторін іншого називаються...

А) Вертикальні. Б) Суміжні. В) Розгорнуті. Г) Прямі.          

б) Знайдіть  невідомий елемент

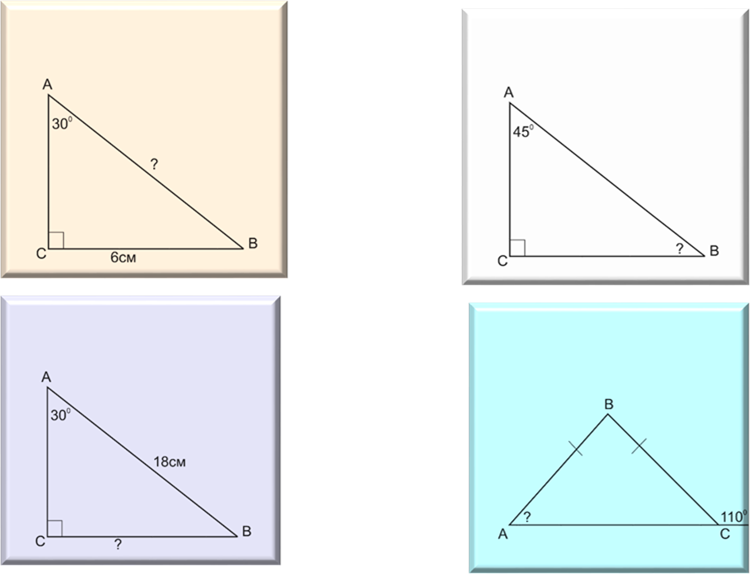
Відповіді:

а) 1.Б)               б) 1. 12см;

2.В)                   2. 45°; 

3.В)                   3. 9см;

4.А)                   4.70°.

II. Мотивація навчання

Вивчаючи коло, вписане в трикутник, ми з’ясували, що точка інцентру (перетину бісектрис) є центром вписаного

кола в трикутник. Постає завдання

з’ясувати, де знаходиться центр і що є радіусом описаного кола навколо трикутника (гострокутного, тупокутного і прямокутного).

III. Вивчення нового матеріалу

Означення. Серединним перпендикуляром до             відрізка називають пряму, яка проходить

через    середину відрізка і перпендикулярна до нього.

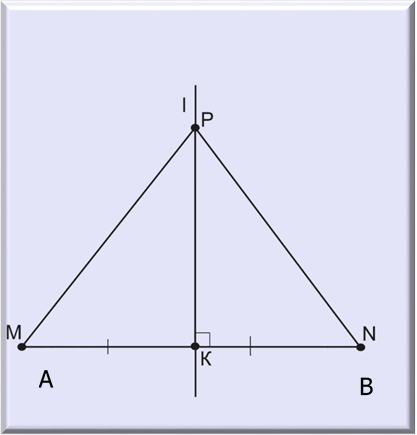Доведення

1)   Якщо Р збігається з К, то рівність РА=РВ

очевидна.

2)   Якщо Р відмінна від К, то розглянемо

∆АРК і ∆КРВ. АК=КВ, бо К – середина АВ,  AКР=

РКВ=90°

КР – спільна

∆АРК=∆КРВ(за двома катетами), то

АР=ВР.   Теорему доведено.

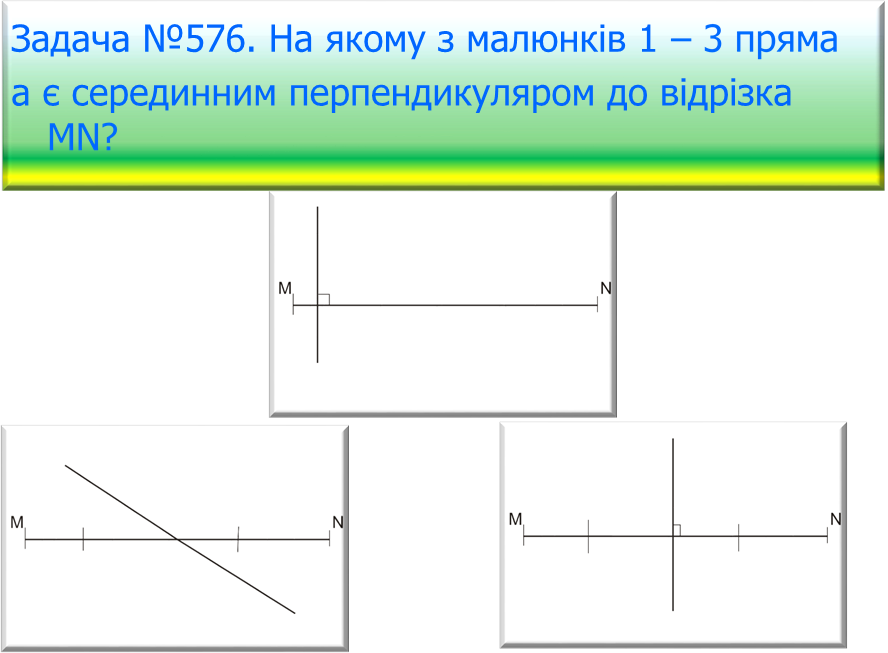
Задача №579.

1)                  Накресліть відрізок MN, довжина якого 5,6см. За допомогою лінійки з поділками та трикутника проведіть серединний перпендикуляр до відрізка MN.

2)                  Позначте деяку точку Р, що належить серединному перпендикуляру і переконайтеся, що PM=PN.



Розв’язання

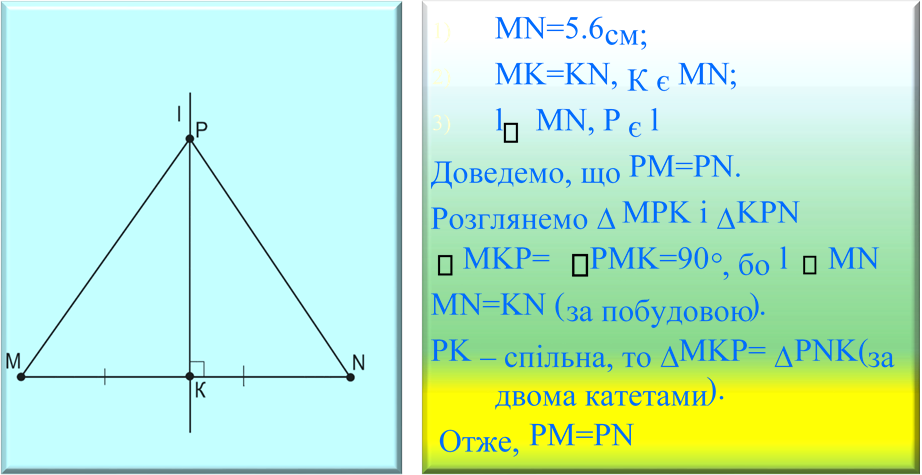
Означення. 

Коло називається описаним навколо трикутника, якщо воно проходить через усі вершини трикутника.

При цьому трикутник називається вписаним у коло.

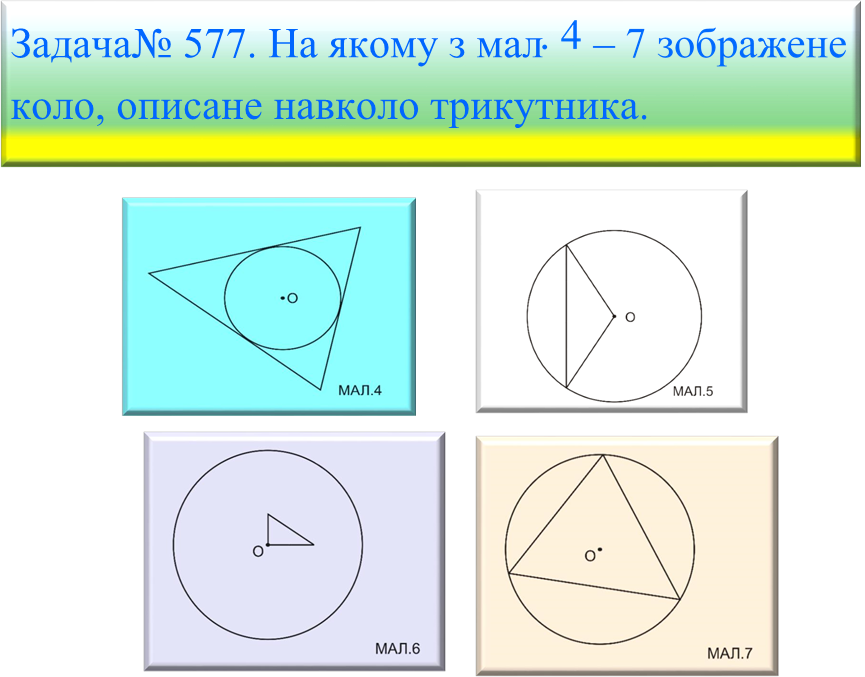
Відповідь: на мал... 7.

Теорема 2 (про коло, описане навколо трикутника).

Навколо будь-якого трикутника можна описати коло.

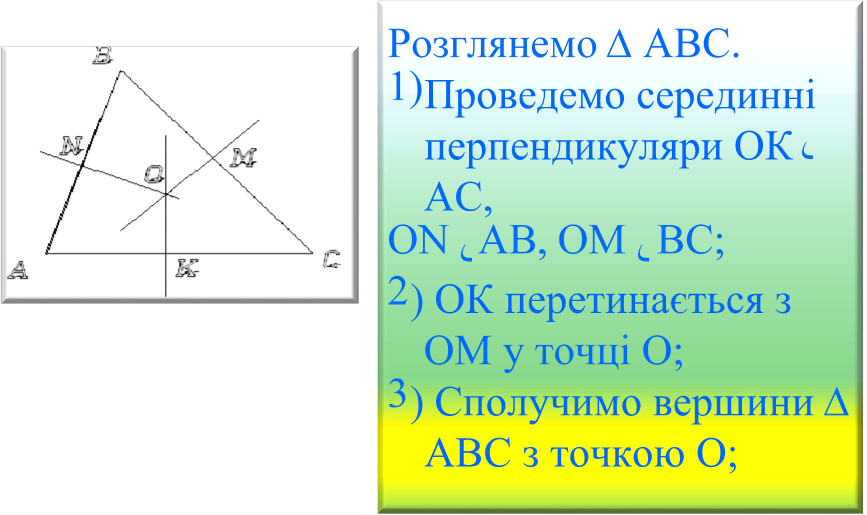
4)Доведемо, що т. О є центром описаного кола навколо трикутника АВС.

а) Оскільки O є NO, NO ل AB, AO=OB;

б) Аналогічно ОА=ОС, оскільки О є ОК, ОК  لАС;

в) ОА=ОВ=ОС

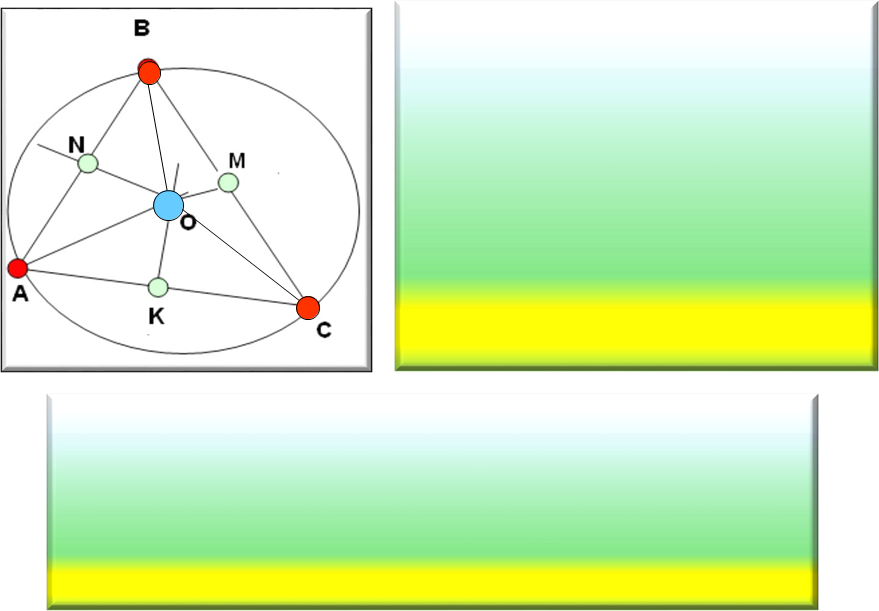Тому коло з центром у точці О і радіусом ОА проходить через вершини А,В і С трикутника АВС. Отже, це коло є описаним навколо ∆ АВС.

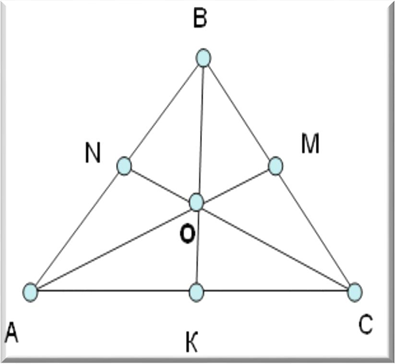
Наслідок 1. Серединні перпендикуляри до сторін трикутника перетинаються в одній точці.

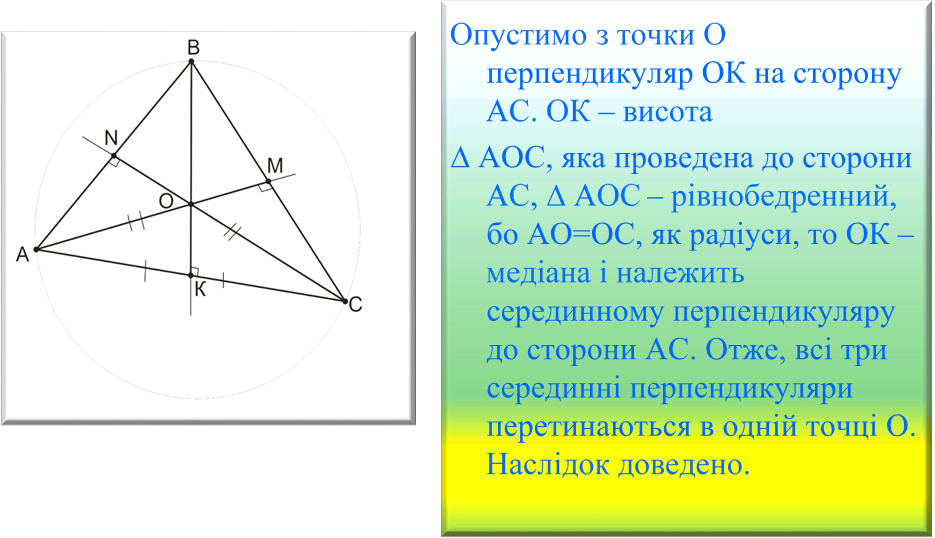Доведення

Наслідок 2.

Центром кола, описаного навколо трикутника, є точка перетину серединних перпендикулярів до його сторін.

Задача №583.

1)                    Накресліть тупокутний трикутик. За допомогою креслярських інструментів опишіть навколо нього коло.

2)                    Де розміщено центр кола (поза трикутником, усередині трикутника, на одній з його сторін )

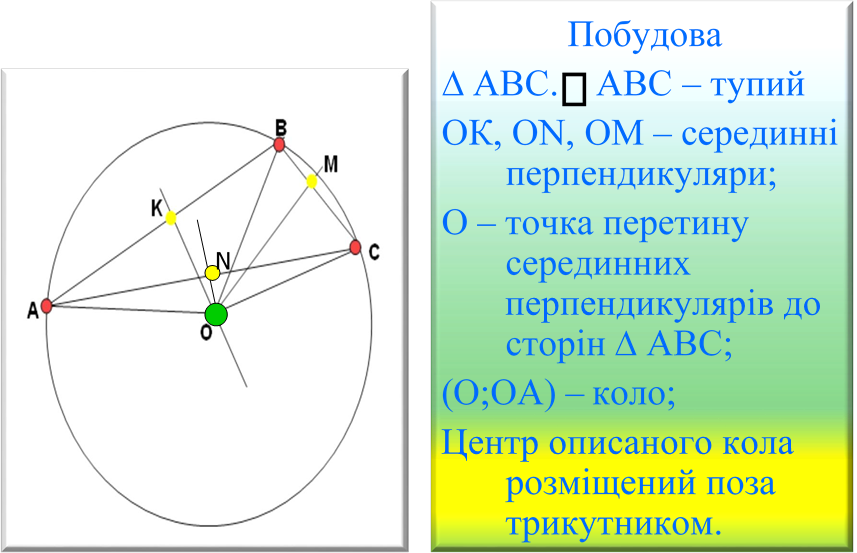
Задача. Довести, що центром кола, описаного навколо прямокутного трикутника, є середина гіпотенузи.

Доведення

∆ АВС,     А CВ=90^◦, СО – медіана, СО=1/2 АВ (за властивістю медіани прямокутнього трикутника, проведеної до гіпотенузи).

Оскільки, АO=ОВ, то СО=АО=ОВ. Точка О – рівновіддалена від вершин ∆ АВС.

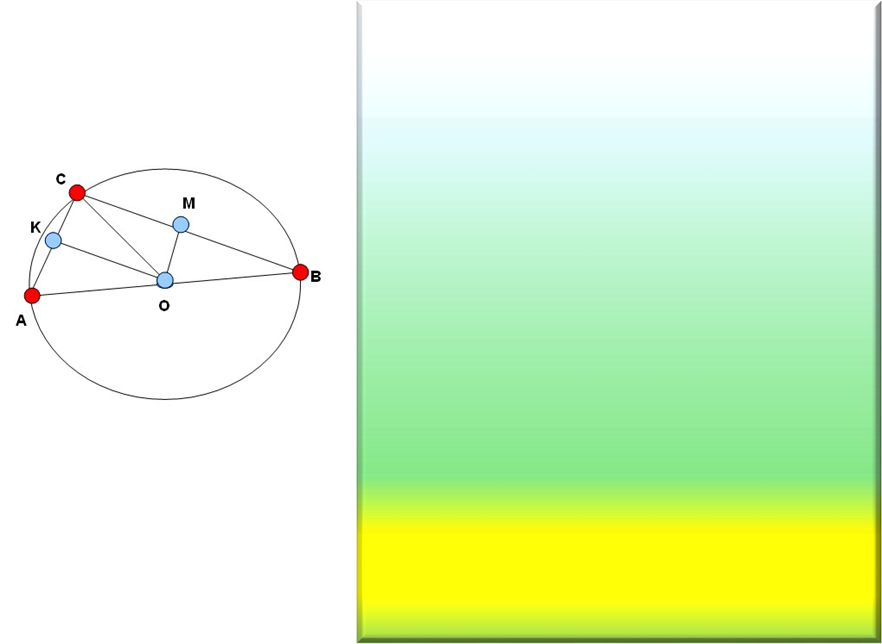Тому коло, центр якого точка О, а радіус ОА, проходить через всі вершини ∆ АВС. Отже, коло, центр якого середина гіпотенузи, а радіус дорівнює половині гіпотенузи, є описаним навколо прямокутного трикутника АВС.

Задача № 587. Доведіть, що радіус кола, описаного навколо рівностороннього трикутника, удвічі більший від радіуса кола, вписаного в нього.

Розв'язання.

∆ АВС, АВ=ВС=АС, ОК, ОМ, ON – серединні перпендикуляри. АО=ОС=ОВ – радіус

описаного кола, де О – центр кола. АМ, ВК, CN – медіани і висоти, то

ОК=ОM=ON – радіус вписаного кола; О – центроїд, то

АО=2ОМ.

Домашнє завдання:

вивч. §24, повт. §15 №577, 580, 584.

Підсумок уроку.

1.     Що називається серединним перпендикуляром?

2.     Сформулювати властивість серединного перпендикуляра до відрізка.

3.     Яке коло називається описаним навколо трикутника?

4.     Підрахунок жутонів.