УРОК  З ГЕОМЕТРІЇ

в 10 класі

з використанням інтерактивних технологій

 

 

 

                                      ЯКОВЕНКО  ЛЮДМИЛА

                                             ПЕТРІВНА,

                                          учитель математики 

                                          опорного закладу   

                                          «Оржицька ЗОШ І-ІІІ ст.

                                                     ім. І.Я.Франка»

 

 

 

 

2018 р.

 

 

УРОК  З ГЕОМЕТРІЇ

в 10 класі

з використанням інтерактивних технологій

 

 

ТЕМА. Систематизація й узагальнення знань з теми: “ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ І ПЛОЩИН У ПРОСТОРІ”.

 

МЕТА.  Закріпити й поглибити знання учнів з теми, повторити вивчений навчальний матеріал;

розвивати навички використання теоретичних знань до розв’язування задач, логічне мислення, творчі здібності, просторову уяву учнів, пізнавальну активність, культуру спілкування, вміння формулювати відповіді на запитання та аналізувати відповіді своїх товаришів;

виховувати наполегливість, гнучкість мислення, інтерес до геометрії як науки.

 

ОБЛАДНАННЯ. Інтерактивна дошка, мультимедійна презентація до уроку, моделі, таблиці, роздатковий матеріал.

 

ТИП УРОКУ. Урок узагальнення і систематизації знань, умінь і навичок.

 

ФОРМА проведення уроку. Бізнес-гра з використанням інтерактивних технологій “Мікрофон”, “Акваріум”.

 

ХІД  УРОКУ

 

І.Організаційний момент.

 Урок проводиться у вигляді бізнес-гри. Капіталом її учасників є одержані за правильні відповіді бали. Перед кожним з вас лежить банківська кредитна карточка, куди ви й будете заносити одержану валюту – бали за правильні відповіді. Кожен учень одержує бали як за індивідуальні відповіді, так і за роботу в групах, за оцінку роботи своїх товаришів. Як заохочення, по завершенню гри, всі учні, хто отримав більше, ніж 12 балів матимуть за ТО на 1 бал більше, ніж бал за написану контрольну роботу, а переможець гри – на 1 бал більше за семестр.

 На торгових біржах користуються таким терміном – ЛОТ.

ЛОТ – певна кількість товару одного виду (партія товару); одиниця угод на торговій біржі; або найменша сума валюти, яку банк може виставити на валютній біржі.

 Ми користуватимемось цим терміном при розв’язуванні завдань різних типів.

 

ІІ. Оголошення теми, мети уроку, мотивація навчання.

 Вступнне слово вчителя.  У 10 класі ми почали вчити новий розділ геометрії – стереометрію.Ви вже зробили кілька кроків на шляху пізнання цієї науки – стереометрії. Ці кроки вимагали від вас наполегливості, зосередженості, логічних міркувань. Ви вивчили аксіоми стереометрії та їх найпростіші наслідки, паралельність прямих і площин у просторі. І ось ми закінчуємо вивчати ще одну тему: “Перпендикулярність прямих і площин у просторі”. На сьогоднішньому уроці ми повинні систематизувати, узагальнити знання з цієї теми, показати вміння застосовувати теоретичний матеріал при розв’язуванні задач.

 Отже, тема сьогоднішнього уроку: “Перпендикулярність прямих і площин у просторі”.

 

             (На екрані з’являється перша сторінка презентації)

 Зверніть увагу на слова Рене Декарта (французький математик, 1596-1650) “Недостатньо мати добрий розум, головне – це раціонально застосовувати його”.

 

 

 

ІІІ. Актуалізація опорних знань і чуттєвого досвіду учнів.

ЛОТ - 1

1. Сформулювати й довести такі теореми:   ( 6 балів за відп.)

 

Теорему про три перпендикуляри (т.3.5)

 

Ознаку перпендикулярності площин (т.3.6.)

 

Інші учні аналізують відповіді товаришів, одержуючи за це по 2 бали.

2.      Усне опитування  теоретичного матеріалу проводить хтось із учнів ( 6 балів ), а кожен учень записує у свій актив по 1 балу за правильну відповідь. За неправильну відповідь бали віднімаються.

 

( ПЕДТЕХНОЛОГІЯ”Мікрофон”)

 

 

 

 

ІV. “Знайди істину”  Розв’язування міні-задач на розвиток просторової уяви учнів.

 

 Повне пояснення і обгрунтування з використанням означень і теорем – 3 бали;

   Правильне пояснення – 2 бали;

 Правильна відповідь без пояснення – 1 бал.

ЛОТ - 2

 

1. Чи можуть дві різні площини мати лише одну спільну точку?  ( Ні, акс.С₂)
2. Чи правильно, що коли пряма не перпендикулярна до площини, то вона не перпендикулярна до жодної прямої у цій площині? ( Ні, пряма може бути похилою до площини і одночасно буде перпендикулярна до прямої у цій площині ).
3. Через одну із сторін трикутника можна провести площину, перпендикулярну до другої сторони. Який це трикутник?  (Прямокутний )
4. Площина  перпендикулярна до прямої  в, а пряма в паралельна прямій с. Яке взаємне розміщення площини  і прямої с? (с, т.3.3.)
5. Пряма а перпендикулярна до площини , а площина  паралельна до прямої с. Яке взаємне розміщення прямих с і а ?  ( Прямі а і с мимобіжні або перетинаються в одній точці )
6. Скільки прямих, перпендикулярних до даної площини, можна провести через точку поза даною площиною? (Одну)
7. Площина  перпендикулярна до прямої в, а пряма в перпендикулярна до прямої с. Яке взаємне розміщення площини  і прямої с? (с//)

 

 

 

 

 

 

 

 

 

 

 

 

 

V. “Не вір очам своїм”   Задачі  для усного розв’язування за готовими малюнками.  ( 3 бали)

ЛОТ - 3

 Вам відомо, що для зображення просторових фігур на площині ми використовуємо паралельне проектування. І дійсності не завжди відповідає те, що ми бачимо, а істину треба доводитьи і обгрунтовувати.

 

 

 

 

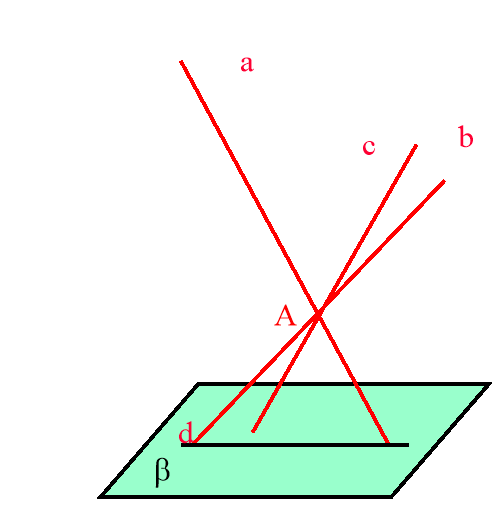
1. Чи лежать прямі а, в, с в одній площині?

 

 

(Ні. Якби ці три прямі лежали в одній площині , то пряма с перетинала б площину  у прямій l, лінії перетину площин  і ).

 

2. Ввідомо, що АВСD –квадрат, SA(ABC). Що ви можете сказати про трикутник  SDC? Відповідь обгрунтувати.

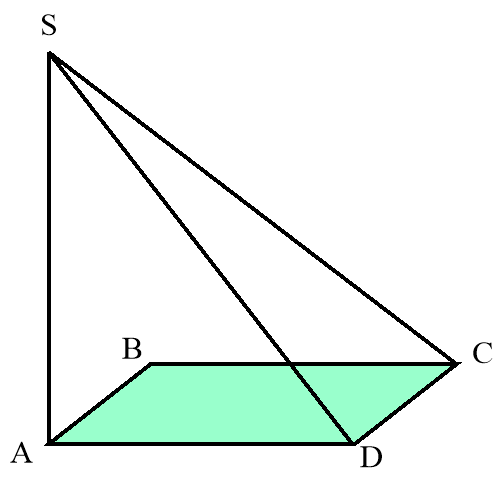
( Трикутник SDC  прямокутний. SA(ABC), SD –похила, AD –її проекція. Оскільки ADCD ( як сусідні сторони квадрата ), то за теоремою про три перпендикуляри SDCD.)

 

 

 

 

 

 

 

 

 

 

 

 

VI.  Тестове опитування учнів.

Кожне завдання тесту оцінюється по 0,5 бала. По закінченню тестування учні, які сидять за однією партою, міняються зошитами і перевіряють роботи один одного. Правильні відповіді учитель демонструє на інтерактивній дошці.

 

ЛОТ - 4

1.  Дві різні площини мати лише одну спільну точку? Це так чи ні? (Ні).
2. Чи можна стверджувати, що будь-які дві точки завжди лежать на одній прямій? (Так).
3. Чи можуть бути паралельними площини, які проходять через не паралельні прямі? (Так).
4. Чи можна при паралельному проектуванні прямокутника отримати трапецію? (Ні).
5. Чи можна при паралельному проектуванні паралелограма одержати квадрат? (Так).
6. Чи правильно, що коли пряма не перпендикулярна до площини, то вона не перпендикулярна до жодної прямої у цій площині? (Ні).
7. Чи можна стверджувати, що будь-які чотири точки завжди лежать в одній площині? (Ні).
8. Пряма а паралельна до прямої в, а пряма в паралельна до площини . Чи обов’язково пряма а паралельна до площини ? (Так).
9. Чи правильно, що дві мимобіжні прямі мають спільний перпендикуляр? (Так).
10. Чи можна стверджувати, що через пряму і дві точки поза нею можна провести площину? (Ні).
11. Перпендикуляром, опущеним з даної точки на дану площину, називається відрізок, що сполучає дану точку з точкою площини. Чи так це? (Ні).
12. Чи правильно, що відстанню між мимобіжними прямими називається довжина їх спільного перпендикуляра? (Так).

 

 

 

 

VII. РОЗВ’ЯЗУВАННЯ ТЕКСТОВИХ ЗАДАЧ

ЛОТ - 5

 

(ПЕДТЕХНОЛОГІЯ”Акваріум”)

 

 

1.       ABCD –прямокутник,  сторони якого 6 см і 15 см. KA(ABC), КА=8 см. Знайти відстань від точки К до сторін ВС і CD прямокутника.

Розв’язання.

 

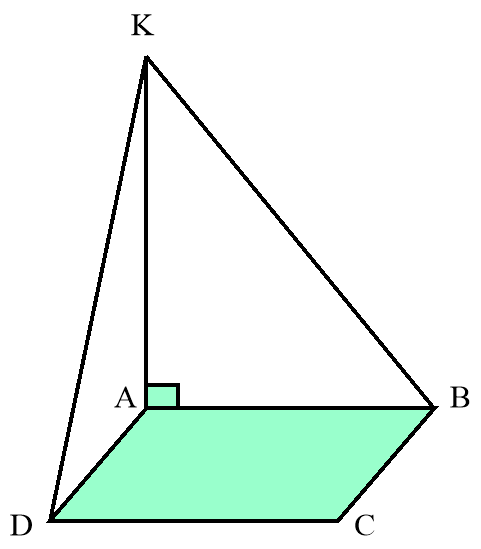
  КА(АВС), КВ – похила, АВ – її проекція. АВВС (як сторони прямокутника), то за теоремою про три перпендикуляри КВВС, то КВ – відстань від точки К до сторони ВС.

 Із прямокутного трикутника КАВ за теоремою Піфагора визначимо КВ:

                        КВ² = АК² + АВ²

         КВ² =8² + 15² =64 + 225 = 289

       КВ = 17 см.

 Аналогічно KDDC, то KD – відстань від точки К до DC.

 Із прямокутного трикутника KAD за теоремою Піфагора визначимо KD:

      KD² = AK² + AD²

      KD² = 8² + 6² = 64 + 36 =100

      KD = 10 см.

 

  

 

2.       (110(а)). Кінці відрізка, довжина якого дорівнює 24 см, належать двом перпендикулярним площинам. Відстані від кінців відрізка до лінії перетину даних площин відповідно дорівнюють 12 см і 122 см. Обчислити кути, утворені відрізком з цими площинами.

 

Розв’язання.

 

  Нехай кінці А і В заданого відрізка належать площинам  і  відповідно, А₁ і В₁ – проекції точок А і В на площини  і  відповідно. Оскільки ,  А₁В₁ – лінія перетину цих площин, то за опорною задачею 58   ВВ₁, АА₁. Отже, АВА₁ і АВВ₁ – прямокутні. Тоді 

                    sinВАВ₁=ВВ₁/АВ=1/2,  ВАВ₁=30⁰,

 

          sinАВА₁=АА₁/АВ=2/2,  АВА₁=45⁰.

 

 

3.       (94(2)) Точка М рівновіддалена від сторін правильного трикутника і знаходиться на відстані 63 см від площини трикутника. Кут між перпендикуляром і похилою, проведеними із точки М до площини цього трикутника, дорівнює 60⁰. Знайти сторону цього трикутника.

 

Розв’язання.

 

  Нехай АВС – даний трикутник., МО – перпендикуляр, опущений  на площину АВС, МКАС, МLAB, MNDC і точки K, L, N належать сторонам АС, АВ, ВС відповідно. За умовою задачі МК =MN = ML = 123. Оскільки MOK = MOL = MON = 90⁰ ( за означенням прямої, перпендикулярної до площини ), то  MOK = MOL = MON, тому

OK = OL = ON. За теоремою про три перпендикуляри OKAC, OLAB, ONBC, тому точка О є центром кола, вписаного в даний правильний трикутник. Отже, ON = r = a3/6, де а = ВС. Із трикутника MON маємо:

 

   ON²  = MN² – MO²  = 18 (см),

   ВС = 363 (см).

 

4. Відомо, SO(ABC), SA=SB=SC, ABC – прямокутний, С=90⁰. Пояснити розміщення точки О.

 

Розв’язання.

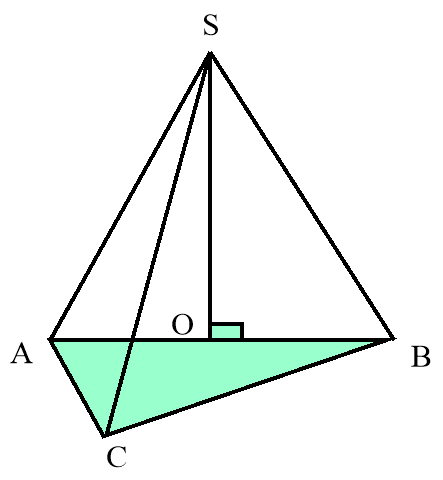
  Точка О – центр кола, описаного навкодло прямокутного трикутника, є есрединою гіпотенузи.

 

VIII. ПІДСУМОК УРОКУ.

 Підводиться підсумок гри, визначаються переможці, отримані бали виставляються у журнал та щоденники учнів.