Урок з геометрії на тему: «Розв'язування трикутників. Систематизація та корекція знань і вмінь», 9 клас

Урок  з  геометрії в 9 класі

Тема уроку. Розв'язування трикутників. Систематизація та корекція знань і вмінь.

Мета уроку: систематизувати знання учнів з теми, формувати уміння і навички розв'язування вправ; розвивати логічне мислення; виховувати самостійність і колективізм; готувати учнів до тематичної атестації.

Обладнання: таблиця ,, Розв'язування трикутників".

Методи інтерактивного навчання. «Мікрофон». «Навчаючи – вчуся», «Мозковий штурм», «Коло ідей».

План уроку

/. Перевірка домашнього завдання.

 Перевірити наявність домашнього завдання та правильність його розв’язання . Актуалізація опорних знань.

І • Ф ронтальне опитування учнів.

1 ) Сформулюйте теорему косинусів.

2.   Чому дорівнює сума квадратів діагоналей паралелограма?

3.   Сформулюйте теорему синусів.

4.   Чому дорівнює радіус R кола, описаного навколо трикутника?

  2. Усні вправи.

1 )Для трикутника ABC справджується рівність а² =  b² + с² – bс

. Чи можна щось стверджувати про величину кута А цього трикутника?

2. Що можна сказати відносно величини кута С трикутника ABC, якщо виконується рівність с²= а² + b² + ab?

3. Чи можна застосовувати теорему косинусів до рівностороннього трикутника ? Дайте пояснення.
4. Застосуйте теорему синусів до трикутників на малюнках. Знайдіть невідомі елементи.

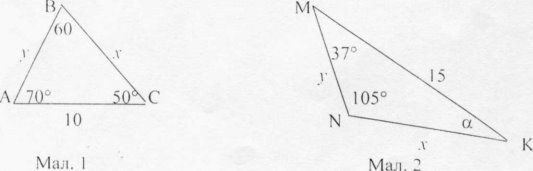
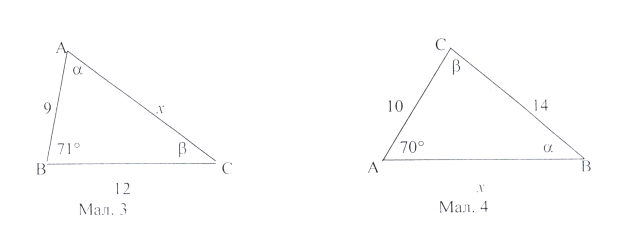
5) Чому дорівнює радіус кола, описаного навколо трикутника ABC

в

Мал. 5

6) Як за допомогою теореми синусів довести, що радіус кола, описаного навколо прямокутного трикутника, дорівнює половині гіпотенузи?

III.Розв'язування вправ.

1 Математичний диктант.

1. Якщо в трикутнику ABC відомі дві сторони b і с та кут між ними А, то третя сторона дорівнює ... .
2. Якщо в  трикутнику відомі сторона а і два прилеглі до неї кути В і С, то дві інші сторони можна знайти так: ... .

3. Якщо  в прямокутному трикутнику відомі гіпотенуза с і гострий кут А, то катети трикутника дорівнюють : ... .
4. Якщо в трикутнику з прямим кутом С відомі катет а і гострий кут В, то другий катет і гіпотенузу можна знайти так: ... .

Розв'язання вправ і захист своїх розв'язків учні проводять біля дошки.

Робота в групах.

Клас поділено на групи по 4-5 учнів. Кожна група одержує диференційовані завдання. Учні колективно розв’язують вправи, обгрунтовують, пояснюютьть розв’язки

Після цього один з учнів групи ( за вибором вчителя), або кожне завдання інший учень, розв'язують біля дошки з повним обгрунтуванням. Учні іншої групи ставлять запитання щодо розв'язання. ( можливий інший варіант перевірки).

Картка № 1 (№3)

І рівень

1. Квадрат будь-якої сторони трикутника дорівнює ... .
2. У трикутнику проти більшого кута ... .
3. Знайти х:

4.

5. Який кут найбільший?

ІІ рівень.

6. Як, маючи довжини сторін трикутника а, Ь, с, можна дізнатися, якого виду трикутник: ( гострокутний, тупокутний, прямокутний) ? Пояснити.

ІІІ рівень

7. Сторони паралелограма дорівнюють 7 см і 9 см, а діагоналі відносяться як 4 : 7. Обчислити діагоналі паралелограма.

Картка № 2 ( №4).

1 рівень

1. Сторони трикутника пропорційні ... .
2. У трикутнику проти меншої сторони ... .
3. Знайти х :

5. Який кут найменший?

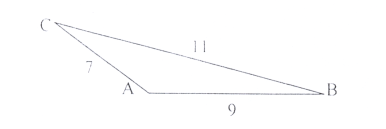
ІІ рівень.

6. Якого виду трикутник зі сторонами 10, 24 і 26 см?

ІІІ рівень

7. Діагоналі паралелограма дорівнюють 7 см і 11 см, а сторони відносяться, як 6: 7. Обчислити периметр паралелограма.

3. Колективне разв 'язування задачі

У трикутнику медіана, проведена до основи, довжина якої 13 см, дорівнює 8 см. Визначити меншу сторону трикутника, якщо його бічні сторони відносяться, як 3:5.

Разв’ язання.

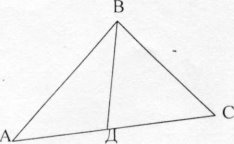
Нехай ВС = 3х см, АВ - 5х см ( х> 0). АД = ДС = АС = • 1 3 = 6.5 (см)

У ∆ АВД за теоремою косинусів АВ² = АД² + ВД² - 2 • АД • ВД • cos ∟AДB.  

                         ( 5х)² = 6,5² + 8² - 2 • 6,5 • 8 • cos а.

У ∆ ВДС       ВС² = ВД² +ДС²  -    2 • ВД • ДС • cos ∟ВДС (теорема косинусів).

                      ( Зх)² = 8² +6,5² - 2 ∙ 8 • 6,5 • cos( 180° - а );

                                 cos (180° - а ) = - cos а.

Отже, маємо 25х² = 42,25 + 64 - 104 cos а,

                      9х² = 64 + 42,25 + 104 cos а.

        Звідси, 25х² + 9х² = 212,5;

                       34х² = 212,5;

                          х²:= 6,25;

                          х = 2,5 (х>0).

 ВС = 3х = 3 • 2,5 = 7,5 (см).             Відповідь:  7,5 см.

IV. Завдання додому.

Повторитн п. 109 - 1 12, вправи 15, 16,   ст. 179.

V. Підсумок уроку.