Урок з математики для 6-го класу на тему "Додавання чисел з різними знаками"

Урок № 77

Додавання чисел з різними знаками

Цілі:

 -навчальна: домогтися засвоєння правила додавання чисел з різними знаками; сформувати вміння виконувати додавання чисел з різними знаками, розв’язувати задачі, які передбачають додавання чисел з різними знаками;

 -розвивальна: розвивати математичну компетентність, творчі здібності, кмітливість учня;

 -виховна: виховувати спостережливість, працьовитість, охайність, акуратність.

Тип уроку: урок засвоєння нових знань, умінь і навичок;

Обладнання та наочність: план-конспект, мультимедійна дошка, ілюстрації до уроку.

Методи: словесні, наочні, практичні.

Форми: індивідуальна робота, колективна.

Хід уроку

I.Організаційний етап (1 хв)

Вчитель вітається з класом, з’ясовує хто відсутній

II. Перевірка домашнього завдання (1 хв)

Правильні відповіді виведені на екран проектора. Діти звіряють домашнє завдання з виконаним в зошиті. Вчитель перевіряє наявність домашнього завдання в зошитах.

III. Формулювання мети і завдань уроку (2 хв)

Вчитель: Сьогодні вранці я отримала повідомлення. Давайте ми його прочитаємо разом! (Вчитель тримає листа і читає). Дорогі учні 6-Б класу! Ми, додатні і від’ємні числа звертаємось до Вас по допомогу. Ми жили спокійно і мирно кожен у своєму королівстві. Але непосидюче число -3 знайшло таємний хід між королівствами «Додатних» і «Від’ємних» чисел. І почався справжній хаос. Додатні числа пішли у королівство «Від’ємних», від’ємні у королівство «Додатних». Але взаємодіяти разом вони не можуть. Кожен хоче жити за своїми законами і не слухає іншого. Допоможіть нам! Дайте нам закони, щоб у наших королівствах знову панував мир! Якщо ви нам не допоможете, то у наших королівствах почнеться війна! З повагою до вас додатні і від’ємні числа.

Ну що, діти, допоможемо двом королівствам?

IV. Актуалізація опорних знань (4 хв)

Давайте спочатку розподілимо наші числа по їхнім королівствам. Ось у мене є різні числа. Їх треба розподілити на додатні і від’ємні. (Розкидаємо по файлам додатні і від’ємні числа).

Діти, давайте ми з вами пригадаємо ті правила, які ми вже знаємо для спільної взаємодії додатних і від’ємних чисел. (Правила кріпляться на дошку)

1. Щоб додати два від’ємних числа, достатньо додати їх модулі і перед ними поставити знак «мінус».
2. Модулем додатного числа і числа нуль є саме це число, а модулем від’ємного – протилежне йому число.
3. Модулем числа називають відстань від початку відліку до точки, що зображує це число на координатній прямій.
4. Два числа, що відрізняються одне від одного лише знаками називають протилежними числами.
5. Серед двох чисел більшим є те, яке на координатній прямій розміщено правіше

Діти, дивіться, в нас немає жодного правила як нам додавати додатні і від’ємні числа. Це і буде темою нашого сьогоднішнього уроку.

V. Засвоєння знань (10 хв)

 Розглянемо приклади на координатній прямій. Маємо число 3. Якщо нам необхідно до нього додати 2, то ми повинні рухатись на 2 одиниці у напрямку додатних чисел, тобто вправо. Отримаємо число 5.

 Якщо нам треба до числа -3 додати число -4, то ми повинні рухатись від числа -3 на 4 одиниці у напрямку від’ємних чисел, тобто вліво. Отримаємо число -7.

  Якщо ж нам треба до числа -4 додати число 5, то ми повинні рухатись від числа -4 у напрямку додатних чисел на 5 одиниць. Отримаємо число 1.

 Розглянемо ще один приклад.

 Припустимо, що в понеділок Іван заборгував Сергію 3 грн, а у вівторок повернув борг, тобто повернув Сергію 3 грн. Оскільки борг можна тлумачити як від’ємні числа, а майно – як додатні числа, то розрахунок між хлопцями можна подати так:

    -3+3=0

 Числа -3 і 3 протилежні, їх сума дорівнює нулю.

Отже, сума двох протилежних чисел дорівнює нулю.

Якщо у понеділок Іван заборгував Сергію 3 грн, а у вівторок повернув 2 грн., то борг Івана Сергію становить 1 грн. Це можна записати так:

     -3+2=-1

 У цій сумі модулі доданків дорівнюють 3 і 2, а модуль суми дорівнює 1, тобто модуль суми дорівнює різниці більшого і меншого модулів. Знак, який стоїть перед знайденим числом (мінус), збігається зі знаком доданка, модуль якого є більшим числом (числа -3).

 Нехай у понеділок Іван заборгував Сергію 3 грн, а ввечері отримав від батька 5 грн. Коли Іван віддасть борг, то в нього залишиться ще 2 грн. Це можна записати так:

    -3+5=2.

 У цій рівності модулі доданків дорівнюють 3 і 5, а модуль суми 2, тобто модуль суми знову дорівнює різниці більшого і меншого модулів. Знак, який стоїть перед знайденим числом (плюс), знову збігається зі знаком доданка, модуль якого є більшим (числа 5).

Маємо правило додавання двох чисел з різними знаками:

 Щоб додати два числа з різними знаками, достатньо від більшого модуля доданків відняти менший модуль і записати перед знайденим числом знак того доданка, модуль якого більший.

 Виконуючи обчислення, зручно спочатку визначити і записати знак суми, а потім у дужках записати різницю модулів.

Приклад:

   -10+7=-(10-7)=-3

   -4+8=+(8-4)=4 або 8+(-4)=8-4=4

-5+5=0

Розглянемо приклад додавання звичайних дробів з різними знаками, в якому спочатку треба порівняти модулі доданків і, лише після цього, застосувати правило:

• .

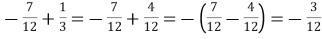VI. Фізкультхвилинка (1 хв)

VII. Формування вмінь (15 хв)

 Відкриваємо підручники, ст. 189, є правило для додавання двох чисел з різними знаками.

 Отже, правило ми з вами сформулювали. Тепер треба показати числам як же їм бути на практиці в різних випадках.

 (Усні вправи) № 1020, 1021, 1022, 1023, 1024

№ 1026 (1, 3, 5, 7, 9)

Задача: Гроші, які потрапляють до казни королівства записують зі знаком «+», а гроші, які витрачаються – зі знаком «-». Порахуйте, чи залишаться в королівстві гроші.

VII. Підсумки уроку (5 хв)

Для того щоб додатні і від’ємні числа подружились і остаточно зрозуміли як їм треба взаємодіяти для того, щоб жити мирно, кожен з нас повинен засвоїти ці правила. Тож виконуємо завдання на картках в парах.

VIII. Рефлексія (2 хв)

Ось ми з вами і сформулювали правило для додавання чисел з різними знаками. Продовжте, будь ласка, речення. На уроці я дізнався…

IX. Домашнє завдання

П 39, №1024, 1027

Список використаної літератури:

1. Істер О.С. Математика: підруч. для 6-го кл. загальноосвіт. навч. закл. / О.С.Істер. – К.: Генеза, 2014. – 296 с.: іл.