Урок з математики "Дотична до кола та її властивості"
Дотична до кола, її властивості
Мета:
навчальна: домогтися засвоєння означення дотичної до кола, теореми про властивість та ознаку дотичної до кола; формувати вміння розв’язувати задачі, які передбачають використання поняття дотичної, її властивості та ознаки;
розвивальна: розвивати абстрактне мислення; формувати вміння виділяти головне в інформації;
виховна: виховувати творчу активність, цілеспрямованість, самокритичність.
Тип уроку: засвоєння нових знань і вмінь.
Обладнання: набір демонстраційних креслярських інструментів.
Хід уроку
І. Організаційний етап.
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
ІІ. Перевірка домашнього завдання.
|
1 |
Колом називають геометричну фігуру, яка |
1 |
хордою. |
|
2 |
Відрізок, що сполучає центр з будь-якою точкою кола, називають |
2 |
перпендикулярний до цієї хорди. |
|
3 |
Діаметр є |
3 |
діаметром. |
|
4 |
Відрізок, що сполучає дві точки кола, називають |
4 |
ділить її навпіл. |
|
5 |
Хорду, що проходить через центр кола, називають |
5 |
складається з усіх точок площини, рівновіддалених від даної точки. |
|
6 |
Діаметр з будь-якої точки кола |
6 |
найбільшою з хорд. |
|
7 |
Діаметр кола, перпендикулярний до хорди, |
7 |
кругом. |
|
8 |
Діаметр кола, що проходить через середину хорди, яка не є діаметром, |
8 |
видно під прямим кутом. |
|
9 |
Коло разом з його внутрішньою областю називають |
9 |
радіусом. |
Учні знаходять відповідність між правою та лівою частинами таблиці. Перевіряється вивчення правил.
ІІІ. Формулювання мети і завдань уроку
Учитель проводить бесіду, у ході якої нагадує учням, що геометрія вивчає як окремі геометричні фігури (відрізок, кут, трикутник), так і відношення між геометричними фігурами (рівність) та різні випадки їх взаємного розташування (паралельність прямих; вертикальні та суміжні кути).
Після чого вчитель може запропонувати за допомогою простих моделей — нарисованого на дошці (або на цупкому картоні) кола та прямої, яка рухається по площині цього кола (нарисована на прозорій плівці пряма або звичайна демонстраційна лінійка), змоделювати різні варіанти взаємного розташування прямої та кола.
З’ясувавши шляхом нескладних випробувань, що можливі три варіанти розташування, учитель повідомляє, що особливий інтерес викликає випадок, коли пряма і коло мають тільки одну спільну точку. У цьому випадку пряма має спеціальну назву — дотична до кола. Завдання уроку: вивчити означення дотичної, її властивість і ознаку.
ІV. Актуалізація опорних знань
Для свідомого сприйняття учнями доведень властивості та ознаки дотичної, слід активізувати знання учнів про:
1) метод доведення від супротивного;
2) теорему про існування та єдиність перпендикуляра до прямої;
3) ознаку рівнобедреного трикутника;
4) означення рівнобедреного трикутника;
5) властивість кутів рівнобедреного трикутника;
6) означення кола та властивість точок кола;
7) теорему про суму кутів трикутника.
Цю роботу можна провести у формі бесіди або в ігровій формі «Закінчи речення».
V. Засвоєння знань
План вивчення нового матеріалу
1. Означення січної кола.
2. Означення дотичної до кола. Точка дотику.
3. Властивість дотичної до кола.
4. Ознаки дотичної до кола.
5. Застосування властивості дотичної до кола.
Дотичну до кола логічно вивчати як випадок взаємного розташування прямої та кола (мають єдину спільну точку). Бажано також розглянути випадок, коли пряма і коло не мають спільних точок.
Властивість дотичної до кола найчастіше використовують для обчислення кутів. Тому після проведеної роботи пропонуємо учням усно розв’язати задачу.
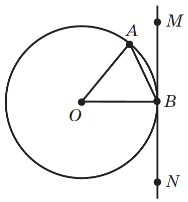
Задача. На рис. 4 MN — дотична до кола з центром у точці O,
∠ABM =40°.
Чому дорівнюють кути трикутника AOB?
|
Дотична до кола |
|
|
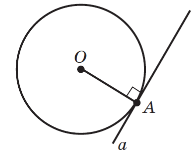
1.Означення. Якщо пряма a має з колом спільну єдину точку A, то пряма a — дотична до кола; A — точка дотику. (Пряма b має з колом дві спільні точки, b — січна.) Пряма називається дотичною до кола, якщо вона має з колом одну спільну точку. Ця точка називається точкою дотику. |
|
|
2. Властивість. Якщо a — дотична до кола (з центром O, радіусом R), A — точка дотику, то OA⊥ a. Дотична до кола перпендикулярна до радіуса цього кола, проведеного в точку дотику. |
|
|
3. Ознака. Якщо пряма a проходить через точку A кола, OA⊥ a (OA — радіус кола), то a — дотична. |
|
VІ. Формування вмінь
Виконання усних вправ
1. AM — радіус кола з центром у точці A, пряма AB перпендикулярна до AM. Чи є пряма AB дотичною до кола?
2. Пряма AB — дотична до кола з центром у точці O, точка дотику позначена буквою M. Яким є трикутник AMO: тупокутним, прямокутним чи гострокутним?
3. Коло з центром O дотикається до сторони AB трикутника ABC у точці M. Кут MBO дорівнює 21°. Чому дорівнюють решта кутів трикутника MBO?
Виконання письмових вправ
1. Пряма AB дотикається до кола з центром O в точці A.
Знайдіть:
1) кут OBA, якщо ∠AOB =20°;
2) радіус кола, якщо ∠AOB =45°, AB=8 см.
2. Через точку кола проведено дотичну й хорду, яка дорівнює радіусу кола. Знайдіть кут між ними.
3. На рис. 5 ∠BOC =150°. Знайдіть кут BAC.
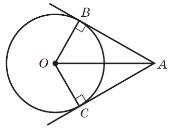
Рис. 5
4. Доведіть, що прямі, які дотикаються до кола в кінцях його діаметра, паралельні.
§17. №589, №601, №609.
VІІ. Підсумки уроку
Фронтальна робота
Знайдіть помилку на рис. 6 у зображенні дотичної AB до кола.
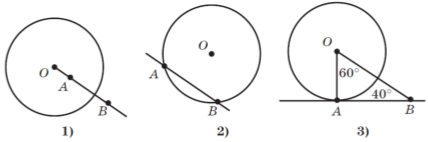
Рис. 6
VІІІ. Домашнє завдання
Повторити теоретичний матеріал за відповідним параграфом підручника. §17.
Дати відповіді на запитання:
1. Пряма AB дотикається до кола з центром O в точці A. Чи може трикутник OAB мати тупий кут?
2. Скільки дотичних до кола можна провести через точку, яка лежить:
1) на цьому колі;
2) усередині круга, обмеженого цим колом?
Розв’язати задачі.
1. Побудуйте коло з центром O і позначте на ньому точку A.
1) За допомогою косинця проведіть через точку A дотичну до цього кола. Яку теорему при цьому потрібно використати?
2) Проведіть хорду AB, яка не є діаметром. Проведіть дотичну до кола в точці B. Позначте точку C — точку перетину двох дотичних — і порівняйте довжини відрізків AC і BC.
2. Пряма AB дотикається до кола з центром O в точці A. Знайдіть кути OBA і AOB, якщо OA=AB.
3. У колі з центром O проведено хорду AB, причому ∠AOB =120°.Знайдіть кут між хордою і дотичною, проведеною до кола в точці B.


про публікацію авторської розробки
Додати розробку