Урок з презентацією на тему "Сума кутів трикутника"

Тема уроку. Сума кутів трикутника

 Формування компетентностей:

• предметна компетентність:  удосконалити вміння застосовувати теорему про суму кутів трикутника та наслідки із цієї теореми;  формувати вміння визначати кількість розв’язків у задачах з рівнобедреним трикутником;

• ключові компетентності:

• спілкування державною мовою – розуміти важливість чітких та лаконічних формулювань; доречно та коректно вживати в мовленні математичну термінологію; зрозуміло формулювати думку, аргументувати , доводити правильність тверджень;
• уміння вчитися впродовж життя - організовувати та планувати свою навчальну діяльність, розвивати самостійність;
• соціальна та громадянська компетентності: співпрацювати в команді,  виділяти та виконувати власну роль у командній роботі. 

Тип уроку: удосконалення і застосування знань і вмінь

Обладнання: конспект уроку, презентація (карта подорожі); кольорові   ілюстрації робіт Ф.К.Айвазовського; декоративне панно «Народження богині краси і кохання», музичний супровід (шум моря)

Хід уроку

І. Організаційний етап

      Учитель. Сьогодні на уроці ми продовжуємо працювати над темою «Сума кутів трикутника» (Слайд 1).

Оголошення мети уроку (Слайд 2)

      Урок проведемо нетрадиційно: запрошую вас у цікаве плавання по Математичному морю (Слайд 3). Щоб воно обуло успішним, потрібен досвідчений капітан. Ви напевно, не будете заперечувати, щоб ним була я. На правах капітана ознайомлю вас з картою маршруту та правилами подорожі.

      Презентація  (Слайд 4). 

      Починаємо подорож із міста Рідна Гавань. Далі повернемо у порт Числоград. Відвідаємо незвичайну країну Нові знання, яка знаходиться на острові з такою самою назвою. Потім прямуватимемо до загадкової країни Розумова розминка. І остання зупинка - Королівство Таємничих чисел. Але нам треба бути особливо обережними, бо саме на цьому етапі подорожі зустрічаються айсберги. І звідси – до Рідної Гавані.

      Слід пам’ятати, що під час морських подорожей трапляються різні перешкоди, до яких ми повинні бути готові. Вам доведеться показати свої знання, бути дуже уважними, старанними, не хвилюватися, щоб вчасно повернутися до Рідної Гавані.

      Спочатку перевіримо вашу готовність до такої подорожі (Слайд 5). 

ІІ. Актуалізація опорних знань

Девіз «Знання збираються по краплині, як вода в долині» (Слайд 6)

Метод «Дивись, не помились» (учні відповідають швидко по черзі)

 (Слайд 7).  

      Запитання:

1. Яку тему ми зараз вивчаємо?

2.  Що називають трикутником?

3. Скільки кутів має трикутник?

4. Залежно від кутів, розрізняють які види трикутників?

5. Залежно від сторін, розрізняють які трикутники?

6. Який трикутник називається рівнобедреним?

7. Яка властивість кутів рівнобедреного трикутника?

8. Який трикутник називають рівностороннім?

9. Що називають медіаною трикутника?

10. Що називають бісектрисою трикутника?

11. Що називають висотою трикутника?

12. Сформулюйте теорему про суму кутів трикутника.

ІІІ. Осмислення раніше вивченого матеріалу

Учитель. Відправляємося у подорож на вітрильнику «Евклід». Зручно розміщуйтеся в каютах вітрильника. (Слайд 8)

Девіз «Один розум добре, а декілька – краще» (Слайд 9)

1.Робота в групах

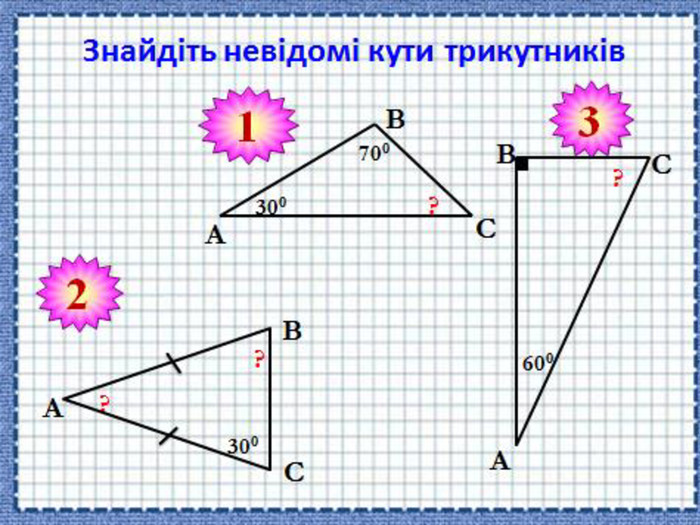
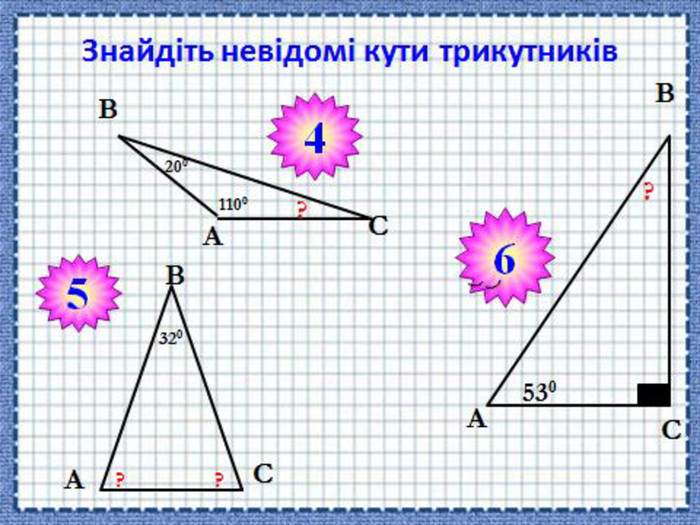
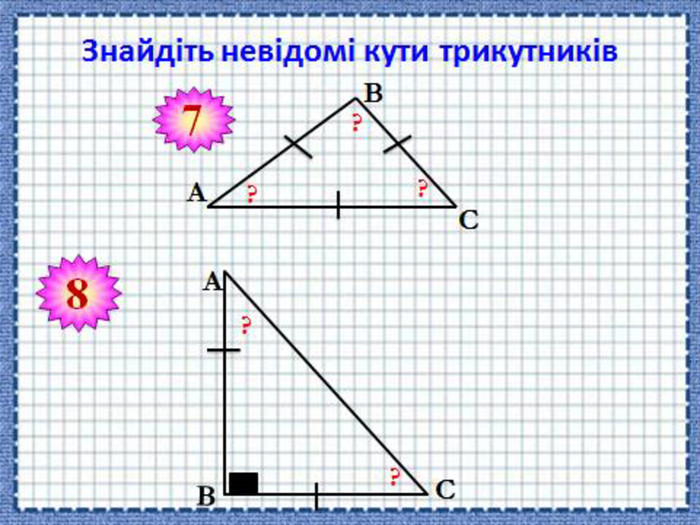
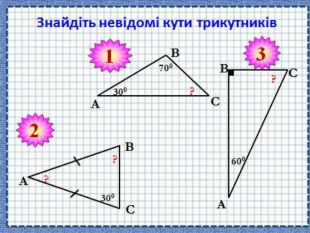
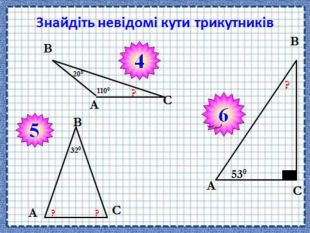
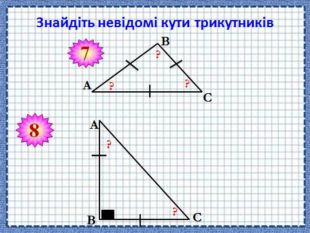
(Учнів об’єднують у гетерогенні, різні за рівнем знань групи). За 2 хвилини потрібно виконати завдання на картках, різних за кольором. Знайти невідомі кути трикутника  (Слайд 10-11).

Картки перевіряють зі слайду.

Вчитель. А тепер? (Слайд 12)

2. Картка-перепустка до півострова Числоград.

Вставте пропущені рисунки та записи.

Ми дібралися до півострова Числоград. Що там лише не обчислюють!

Девіз «Думай голова, куплю картуза» (Слайд 13)

3. Розв’язування задач

Задача 1. Знайдіть усі кути трикутника, якщо один 40°, другий – на 20° більший від даного (Слайди 11-12). 

Задача 2. Знайдіть невідомі кути рівнобедреного трикутника, якщо:

а) кут при основі дорівнює 40°;

б) кут, протилежний його  основі, дорівнює 40° (Слайди 13-17).   

4. Робота з підручником (Слайд 18). 

Завдання  № 415

3х + 4х + 5х =180°

12х = 180°

х = 180°:12

х = 15°

Отже, кути трикутника дорівнюють відповідно: 3·15° = 45°; 4·15° = 60°; 5·15° = 75°

Відповідь. 45°; 60°;75°

Завдання  № 416

х+2(х+15°)=180°

х+2х+30°=180°

3х=150°

х=50°

Отже, кут при вершині дорівнює 50°, а кути при основі: 50°+15°=65°

Відповідь. 50°; 65°.

Завдання  № 420

Нехай градусна міра одного із кутів дорівнює х, другого – х+14°, а третього - 80°. Сума кутів трикутника дорівнює 180°. Маємо рівняння:

80°+ х+ х+14°=180°

2 х=180°- 94°

2 х=86°

х= 43°

Отже, невідомі кути трикутника дорівнюють відповідно: 43° та 43°+14°=57°

Відповідь.  43°; 57°.

Додатково: Завдання № 420,  № 424

5. Нові теоретичні знання(Слайд 19).

    Зараз ми прибуваємо до загадкової країни Нові знання (Слайд 20). Тут ніхто не сидить без діла. Декому доводиться працювати і вночі. Всі жителі мають дивний зв'язок із математиками минулого. Від них вам картка з теоретичним матеріалом.

Розглянути задачі

6. Хвилинка відпочинку (Слайд 21).

     Вчитель. Тепер ми можемо й відпочити  (Слухають шум моря).

Вийдемо на палубу, зручно розмістимося на ній і розслабимося. Помилуємося красою моря (Слайди 22-23). Сонце приємно нас зігріває, тепленький вітерець обвіває обличчя. Прислухаємося до шуму моря та вдивимося в нього. Вода особливого кольору й запаху. Таку красу можна побачити на полотнах видатного мариніста Івана Костянтиновича Айвазовського. (Демонстрація репродукції). Він писав Чорне море у різний час і погод, бо мав для цього можливості, оскільки прожив у Феодосії.

    Чи знаєте ви, хто за грецькою міфологією є богинею краси та кохання?

       Афродіта (Cлайд 24). Вона народилася з морської піни в мушлі (черепашці). Грецьке слово «афрос» означає піна.

        Ми вже бачимо, як мерехтить маяк Рідної Гавані. Перевіримо свої сили та з`ясуємо, чи можемо доплисти до неї.

        А ось і човни з рятівними кругами. До човнів і кругів прикріплено завдання (індивідуальна завдання).

7. Індивідуальна робота

Девіз «Живи своїм розумом, але звіряйся з чужим» (Слайд 25)

ІV. Підсумок уроку

Графічний диктант

У таблиці поставити «+», якщо твердження правильне і «-», якщо неправильне:

1). Якщо один кут трикутника тупий, то два інші гострі.

2). Якщо один кут трикутника прямий, то два інші – тупі.

3). Якщо сума двох кутів трикутника 120°, тоді решта - 60°.

4). Кут при вершині рівнобедреного трикутника 80°. Тоді кути при основі по 100°.

5). У рівнобедреному трикутнику може бути лише один прямий кут.

V. Домашнє завдання (Cлайд 26).

 1. Опрацювати теоретичний матеріал §17 (підручник О.С.Істер).

 2. Виконати вправи: 415, 421; (додатково для учнів достатнього та високого

    рівнів) № 425, № 430

VІ. Оцінювання учнів (Cлайд 27).

Пам’ятайте: якщо хочете навчитися плавати, то сміливо заходьте у воду, а якщо хочете навчитися розв’язувати задачі, то розв’язуйте їх.

                                                                                                                 Д.Пойа