Урок з теми "Декартові координати на площині. Відстань між двома точками. Координати середини відрізка"

9 клас. Геометрія. Урок № 1

 

Тема уроку: Декартові координати на площині. Відстань між двома точками.  Координати середини відрізка

Мета уроку:

навчальна: формувати вміння аналізувати, систематизувати та поглибити знання про декартові координати на площині;

розвивальна: розвивати  навики пошукової дослідницької діяльності, вміння слухати, аналізувати, формулювати висновок, захищати свою думку; критичне мислення учнів;

виховна: виховувати  інтерес до вивчення математики, потяг до наукової творчості, позитивні риси характеру: чесність і правдивість, культуру думки і поведінки, наполегливість і силу волі, відповідальність за доручену справу, уміння працювати у команді

Форма проведення заняття: урок

Тип уроку: комбінований

План уроку

Зібратися разом – це початок,

триматися разом – це прогрес,

 працювати разом – це успіх.

                                    Г. Форд

I. Організаційний етап

  Підготовка учнів до роботи на уроці, створення позитивного настрою учнів.

ІІ. Оголошення теми уроку

     Обговорення девізу уроку

ІІІ. Вивчення нового матеріалу.

     Створення проблемної ситуації і її розв’язання.

Проблемні питання:

1. Відстань між двома точками

А) На прямій

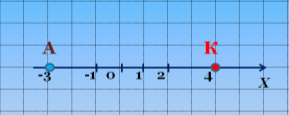
Знайдіть відстань АК (слайд 3).

 

 

 

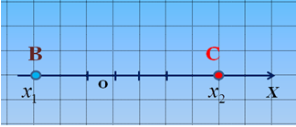Знайдіть відстань ВС (слайд 4).

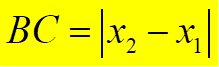
Б) На декартовій площині

Відео про Рене Декарта

https://www.youtube.com/watch?v=72e6Ed0CnL8  (4.58 хв)

 

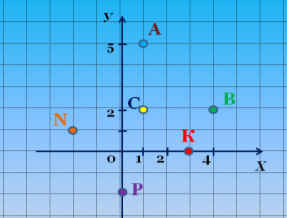
Знайдіть координати

даних точок (слайд 5).

 

 

 

 

Яка відстань між точками В і С?  (Слайд 6)

 

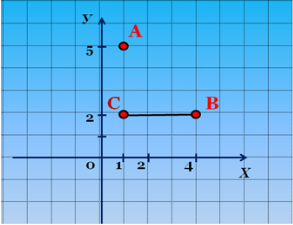
Яка відстань між точками А і С? (Слайд 7)

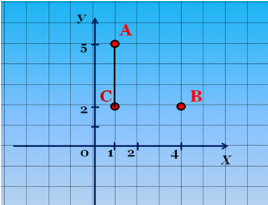
Як знайти відстань між  точками А і В? (Слайд 8)

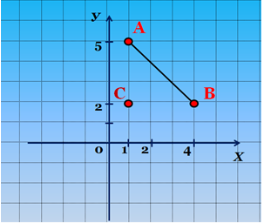
Використовуємо попередні міркування!

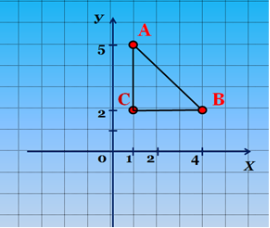
Як же знайти відстань між точками А (х₁; у₁) і В (х₂; у₂), не будуючи самих точок, а знаючи їх координати?  (Слайд 9)

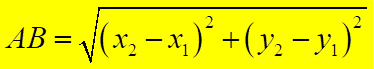
2. Координати середини відрізка

 

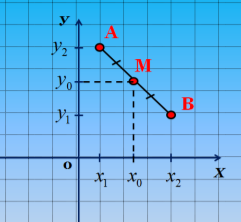
Як знайти координати точки М (х₀; у₀) – середини відрізка АВ, якщо координати точок відомі – А (х₁; у₁), В (х₂; у₂)?

 

 

 

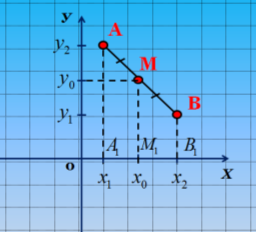За допомогою додаткових добудов отримуємо трапецію А₁АВВ₁.

Чому цей чотирикутник буде трапецією?

Чому ММ₁ є середньою лінією трапеції

 

 

 

 

Розкриваємо модуль і робимо висновок:

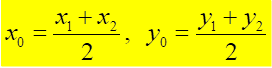
IV. Закріплення вивченого. Робота в групах

Виконати завдання по підручнику і зібрати кодове слово.

№ 8.1.

Знайти відстань між точками: 1) 13; 2) .        О

№ 8.4.

Доведіть, що точка М (0; -1) є центром кола, описаного навколо трикутника АВС, якщо А (6; -9), В (-6; 7), С (8; 5).

Знаходимо сторони трикутника і доводимо, що він прямокутний.

АВ – гіпотенуза, середина гіпотенузи – центр кола, описаного навколо трикутника. Точка М (0; -1) і є центром кола, описаного навколо трикутника АВС.                                            У

№ 8.7(1).

С (1; 6)                                                                 К

№ 8.15.

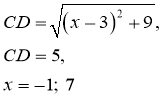                                       Ш

№ 8.16.

Точка С (х; 0) належить осі абсцис, АС = ВС.

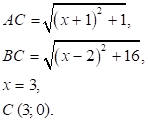П

 

Кодове слово – пошук. Складіть словосполучення із цим словом:

Пошук істини

Пошук нового

Пошук інформації

Пошук друзів

Пошук шляху

Чим важливе це слово для нас?

• Активна взаємодія, самоосвіта, рух вперед!

V. Підсумок уроку

Продовжіть речення:

• Сьогодні я дізнався…
• Було цікаво…
• Було важко…
• Я відчув…
• Я зрозумів…
•  Я тепер можу…
• У мене вийшло…
•  Я спробую…
• Урок навчив мене…
•  Мені захотілось…

 

VІ. Домашнє завдання:

 Вивчити: § 3, п.8

Розв’язати: № 8.2; 8.8; 8.14.

Підручник:

Мерзляк А. Г. Геометрія. Підручник для 9 класу загальноосвітніх навчальних закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. – Харків: Гімназія. – 240 с. – (2017).