Урок з теми: "Функція у=х2"

Тема: Функція у = х² ,  її властивості та графік

Мета: формувати компетентності:

• Предметні: повторити відомості про функції, навчити будувати графік функції у = х² , домогтися засвоєння учнями властивостей функції у = х² .
• Ключові: формувати вміння аналізувати інформацію, бачити закономірності, сприяти розвитку уваги, логічного та абстрактного мислення, усвідомлення необхідності вміти будувати графік функції у = х²
• Загальнокультурні: виховувати  цілеспрямованість, ініціативність, наполегливість, інтерес до вивчення математики.
• Інформаційні: навички роботи з підручником, комп’ютерними платформами.
• Комунікативні: навички спілкування в колективі та толерантне ставлення до думок інших.

Тип уроку: урок вивчення  нового матеріалу.

Обладнання: підручник, мультимедійна презентація.

І. Організаційний етап

Обговорити : критерії оцінювання (роздати картки);

• виконання домашнього завдання;
• яку тему вже вивчили; ( Рац. вирази. Написали к.р. Зробили аналіз)
• приблизний зміст матеріалу, який вивчатимемо ( ст. 117 підр);
• повідомлення теми уроку

ІІ Актуалізація опорних знань

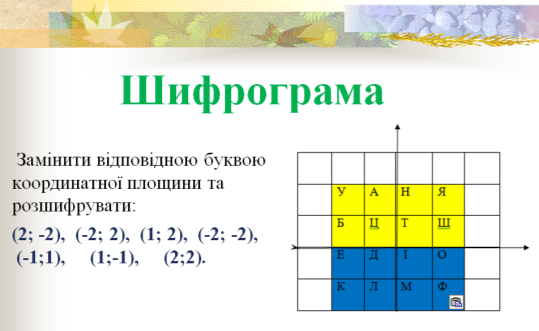
•  Вправа «Шифрограма»

• Назвіть математичні терміни, що асоціюються зі словом «функція»
• Вправа «Асоціативний кущ»
• Назвіть математичні терміни, що асоціюються зі словом «функція»
• Вправа «Незакінчене речення»

• Залежність, при якій кожному значенню змінної х, ставиться у відповідність єдине значення змінної у називають …
• Незалежну змінну ще називають …
• Залежну змінну називають…
• Усі значення, яких набуває незалежна змінна утворюють …
• Усі значення, яких набуває залежна змінна утворюють …
• Координати початку координат…

• Які функції вже вивчали: лінійна, графіком є пряма. Для побудови прямої достатньо двох точок. Обернена пропорційність, графіком є гіпербола. Формула, і де розташовуються вітки, залежно від к.область визначення і область значень.
• Як ми будували графік прямої пропорційності. Складали таблицю значень.

 ІІІ.  Сприймання та первинне усвідомлення  нового матеріалу

• Сторона квадрата –а, площа – s. тоді площа квадрата, а незалежна  змінна – х, залежна – у. Отримаємо функцію у = х²
• Складемо таблицю значень.
• Побудуємо  графік функції. Зрозуміло, що цей графік необмежено продовжується вверх, справа і зліва від осі у.
•     Розглянемо, що ж ми отримали? 
•    Графік цієї  функції  називають параболою. 
• Звідки ж взялась  назва – «парабола», що вона означає?
• Історичний матеріал.

  Древньогрецький математик Аполлоній Пергський за 200 років до нашої ери, розрізавши конус, лінію зрізу назвав параболою, що в перекладі з грецької означає «притча», про що математик і написав у восьмитомнику «Конічні перерізи». І протягом довгого часу параболою назвали тільки лінію перерізу  конуса, поки не з'явилася квадратична функція.

  ІV.  Дослідження властивостей функції

• Дослідження проводимо по графіку усно.

 Робота з підручником, ст 118.

V.  Осмислення та закріплення нового матеріалу

Розв язування вправ.

№ 514 (усно)

№ 515 (1 уч біля дошки)

№ 517 1,2 колективно. Решта самостійно. 3 – усно.

№ 520 (1 уч біля дошки, решта за партою.) Перевіряти. Чим відрізняється від уже побудованого. Назвати область визначення і область значень функції.

№ 521 (1 уч біля дошки, решта за партою.)

Вправа мікрофон.

- Залежність, при якій кожному значенню змінної х, ставиться у відповідність єдине значення змінної у називають …

- Незалежну змінну ще називають …

- Залежну змінну називають…

- Усі значення, яких набуває незалежна змінна утворюють …

- Усі значення, яких набуває залежна змінна утворюють …

- Координати початку координат…

№523 усно по графіку з підручнику.  ( 527)

VІ.  Підсумок уроку і домашнє завдання.

• Вправа « Незакінчені речення»

Залежність, при якій кожному значенню змінної х, ставиться у відповідність єдине значення змінної у називають …

Незалежну змінну ще називають …

Залежну змінну називають…

Усі значення, яких набуває незалежна змінна утворюють …

Усі значення, яких набуває залежна змінна утворюють …

Координати початку координат…

                                          Чи знаєте ви , що

• Траєкторія каменю, кинутого під кутом до горизонту, футбольного або баскетбольного м'яча, що летить,  артилерійського снаряду, є параболою (при відсутності опору повітря). Тож все, що ми кинемо під кутом до горизонту, буде летіти  по параболі, оскільки рух під дією гравітації підкоряється законам квадратичної функції. Учні на дошці роблять малюнок.
• Струмені води фонтана також описують траєкторію у вигляді параболи.
• Форму параболи приймають орбіти комет, супутників та космічних кораблів.
• Парабола володіє оптичними  властивостями: всі промені, що виходять із джерела світла, що знаходиться в фокусі параболі (певна точка), відображені паралельно її осі. Ця властивість параболи використовується при виготовленні прожекторів, автомобільних фар, кишенькових ліхтариків, а також параболічних антен.
• Параболу можна зустріти і в природі.
• Космічні швидкості.
• VII. Оцінювання навчальних досягнень учнів
• VIII. Домашнє завдання

п.13 № 518, 520, 528(1) додатково.